异常检测(Anomaly detection)

建立模型p,类似表示属于正常情况的概率,小于某个值就认为它是异常的。
应用场景
- 诈骗检测
- 异常零件检测
- 数据中心电脑工作情况监控

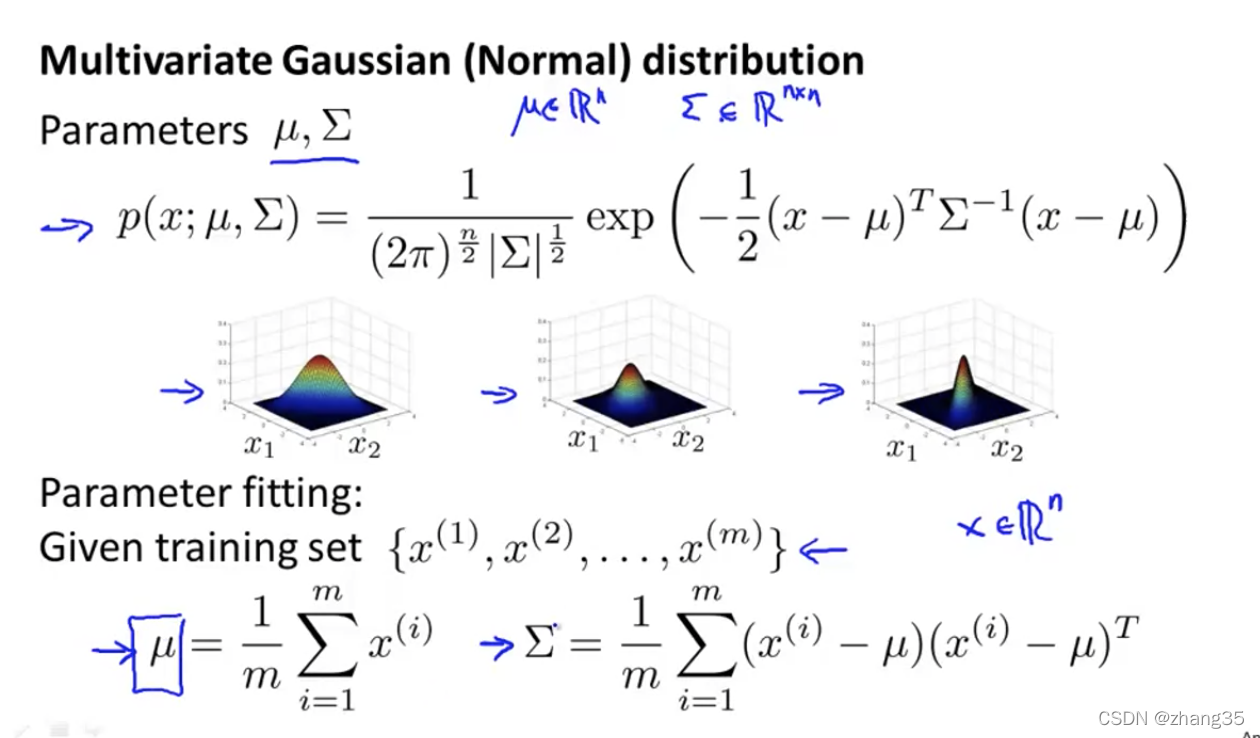
高斯分布 / 正态分布(Gaussian Distribution)

参数估计
给你一组x,假设它们服从高斯分布,计算出μ和σ的值。

这样就能算出新成员的概率。
密度估计
假设x的各个特征是独立的,p(x)就可以用以下公式计算。
计算p(x)的过程也被称为密度估计。

异常检测算法
利用x的密度估计,计算它的概率,看是否小于某值。

具体例子。x1、x2各自的高斯分布,合成左下角三维图像,高度表示概率。山脚下的(粉色)都是低概率点,对应左上图的粉红区域。落在粉红区域的点都可视为异常点。

如何评价异常检测算法
比如如何决定使用哪些特征呢?
假设我们有少量已标记的数据,可以这样分配训练集、验证集、测试集:
60%:20%:20% 的正常样本
0%:50%:50% 的异常样本

有了已标记的数据,就类似于有监督学习了。
回顾一下评判指标,参考https://cloud.tencent.com/developer/article/1486764:
1.混淆矩阵
介绍各个指标之前,我们先来了解一下混淆矩阵。假如现在有一个二分类问题,那么预测结果和实际结果两两结合会出现如下四种情况。
TP、FP、FN、TN可以理解为
TP:预测为1,实际为1,预测正确。
FP:预测为1,实际为0,预测错误。
FN:预测为0,实际为1,预测错误。
TN:预测为0,实际为0,预测正确。

2.准确率
首先给出准确率(Accuracy)的定义,即预测正确的结果占总样本的百分比,表达式为

虽然准确率能够判断总的正确率,但是在样本不均衡的情况下,并不能作为很好的指标来衡量结果。比如在样本集中,正样本有90个,负样本有10个,样本是严重的不均衡。对于这种情况,我们只需要将全部样本预测为正样本,就能得到90%的准确率,但是完全没有意义。
3.精确率
精确率(Precision)是针对预测结果而言的,其含义是在被所有预测为正的样本中实际为正样本的概率,表达式为

精确率和准确率看上去有些类似,但是是两个完全不同的概念。精确率代表对正样本结果中的预测准确程度,准确率则代表整体的预测准确程度,包括正样本和负样本。
4.召回率
召回率(Recall)是针对原样本而言的,其含义是在实际为正的样本中被预测为正样本的概率,表达式为

下面我们通过一个简单例子来看看精确率和召回率。假设一共有10篇文章,里面4篇是你要找的。根据你的算法模型,你找到了5篇,但实际上在这5篇之中,只有3篇是你真正要找的。
那么算法的精确率是3/5=60%,也就是你找的这5篇,有3篇是真正对的。算法的召回率是3/4=75%,也就是需要找的4篇文章,你找到了其中三篇。以精确率还是以召回率作为评价指标,需要根据具体问题而定。
5.F1分数
精确率和召回率又被叫做查准率和查全率,可以通过P-R图进行表示

我们希望精确率和召回率都很高,但现实需要权衡。
F1分数同时考虑精确率和召回率,让两者同时达到平衡最高。F1分数表达式为

上图P-R曲线中,平衡点就是F1值的分数。
异常检测算法里,相当于有了一个倾斜度很高的数据集,应该用精确率、召回率、F1分数来评价。
同样用验证集选择参数ε。

异常检测和有监督学习的区别
- 异常检测的正样本(异常点)数量特别少;
- 异常检测的正样本各种各样,不好拟合;
- 异常检测的测试集可能更加离谱,难以预测;

应用场景:

如何选特征
可以通过hist直方图,看出数据分布是否大致符合正态分布。
对于有偏差的高斯分布,可以做些转换,使它更符合高斯分布:

接下来,如何选特征呢?和有监督学习的交叉验证过程很相似。
验证一下,发现结果不好(左图),就考虑如何增加一个特征,可以使结果变好(右图)。

例子:数据中心主机监测
有时可能陷入死循环,比如一个web服务器的CPU过高,但网络流量不变,就可以增加一个特征X5,或X6:

多变量异常检测
单独来看,低CPU使用没问题,高内存占用也没问题;但二者组合到一起其实是有问题的。
但普通的异常检测画出的是粉色同心圆,检测不出来左上的绿点。

不再分别计算各特征的p(x1)、p(x2)…,直接一把计算p(x):

其中|Σ|是行列式。
determinant:行列式,是一个数值。表示n维几何体的体积。
改变Σ的第k列,就是修改第k维度的方差:

修改左斜的数值,有以下效果,x1和x2正相关,x1 x2同时大时概率才大:

左斜的数值为负数时,x1和x2负相关:


如何计算出多变量高斯分部的μ和Σ:


多变量异常检测使用高斯分布
多变量异常检测算法,使用以下方法计算μ和Σ:
推荐系统
问题定义:影评预测

基于内容的推荐

优化目标,基于线性回归:

当然,训练推荐系统需要同时考虑优化所有θ,即考虑所有用户的感受:

优化函数如下,粉色的是和普通线性回归的区别:

协同推荐
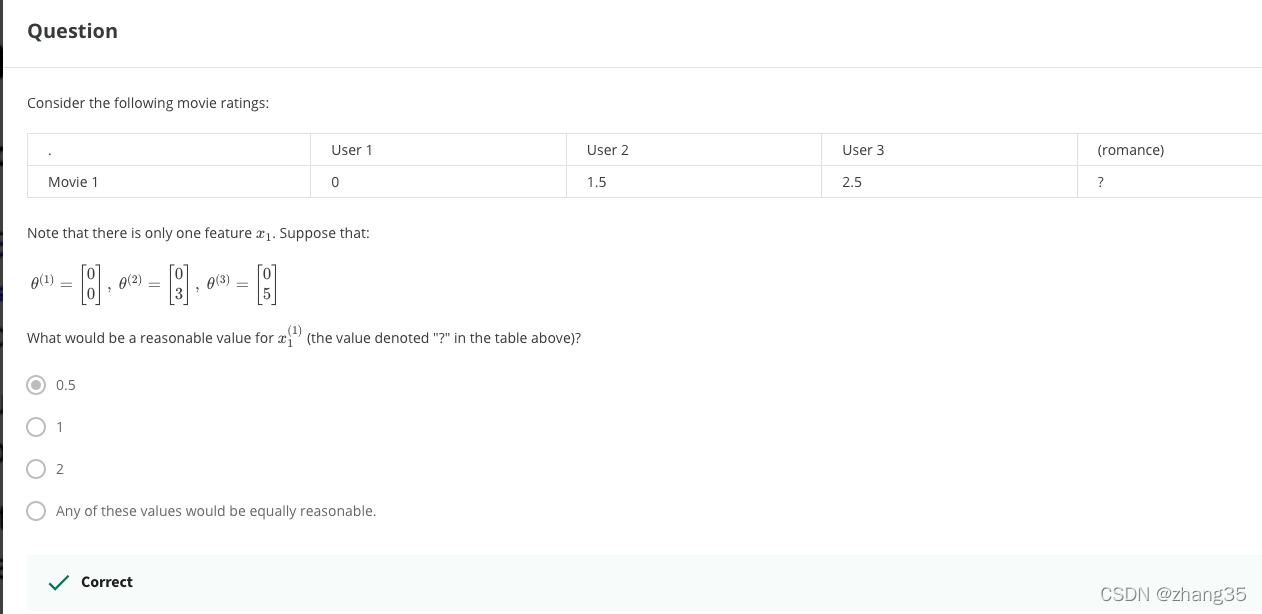
有时知道θ(用户对各种类型电影的偏好),不知道x(电影的类型)。
可以通过θ和y(用户对电影的评分表),求x:

优化函数:
协同过滤
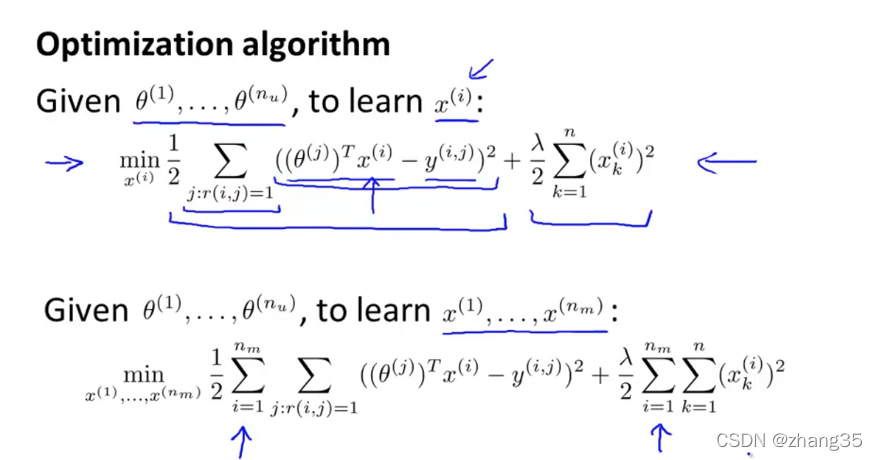
θ和x,知道其一,能得出另一个,变成了先有鸡还是先有蛋的问题。
可以这么做:先猜一些θ,算出来x;用这个x再算θ;循环往复…

所有的用户都在为得出更好的模型贡献力量,所以叫协同过滤。
协同过滤目标函数,同时优化θ和x,不用真的交替搞:





 本文介绍了Coursera上吴恩达的机器学习课程中关于异常检测和推荐系统的知识点。异常检测利用高斯分布进行密度估计,通过设置阈值判断异常点,使用精确率、召回率和F1分数作为评估标准。推荐系统则包含基于内容和协同过滤的方法,通过低秩矩阵分解优化预测。文章还讨论了数据预处理中的均值归一化问题。
本文介绍了Coursera上吴恩达的机器学习课程中关于异常检测和推荐系统的知识点。异常检测利用高斯分布进行密度估计,通过设置阈值判断异常点,使用精确率、召回率和F1分数作为评估标准。推荐系统则包含基于内容和协同过滤的方法,通过低秩矩阵分解优化预测。文章还讨论了数据预处理中的均值归一化问题。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 435
435

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








