算法设计与分析笔记——顶点覆盖问题VC的NP完全性证明

之前在算法设计与分析笔记——NP完全性中总结了证明NPC的思路，本文总结由三元可满足性（3SAT）到顶点覆盖（VC）的NP完全性证明。

定义

3SAT：合取范式中每个简单析取式恰好有3个文字，则称之为3元合取范式。给一个3元合区范式F，问F是可满足的吗？

顶点覆盖：任给一个无向图G=<V, E>，再给一个非负整数K<=|V|，问G中有顶点数不超过K的顶点覆盖吗？

思路

1、显然VC∈NP，因为可以在O(n ^ 2)（n是顶点数）的多项式时间内检查所有的边，看是否包含了所有顶点。

2、把3SAT当成已知的NPC问题，接下来尝试把3SAT规约到VC，若VC比3SAT还难，那必然也是NPC。

证明

取3SAT的一个实例F，向着VC问题变换。

使用构件设计法，构造两组连接：

第一组，把每个文字与它的非连起来，称为变元构件，这组边集记为E1：

第二组，把每个括号中的三个文字如（xi, xj, xk）连起来，称为简单析取构件，这组边集记为E2：

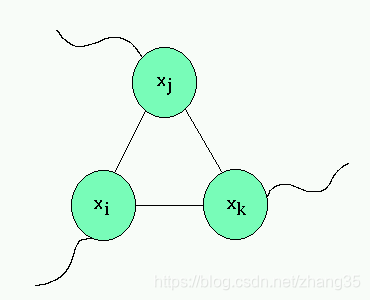
最后把这两组中相同的文字连起来，这组边集记为E3。

例如由F = (x1 V x1 V x2) ∩ (!x1 V !x2 V !x2) ∩ (!x1 V x2 V x2) 构造出下面的图G：