logistic回归二分类

参考：https://www.cnblogs.com/earendil/p/8268757.html

关键步骤：

1. 找到合适的预测分类函数，一般使用sigmoid函数，输入数据得到一个(0,1)区间的值，即为分为1类的概率。
2. 构建损失函数Cost。表示预测结果与真实结果之间的偏差。综合考虑所有训练数据的损失，将Cost求和取平均，记为
3. 找到使最小的值。越小说明预测结果越准确。使用梯度下降或梯度上升法。

具体过程：

1.预测

使用sigmoid函数作为预测分类函数：

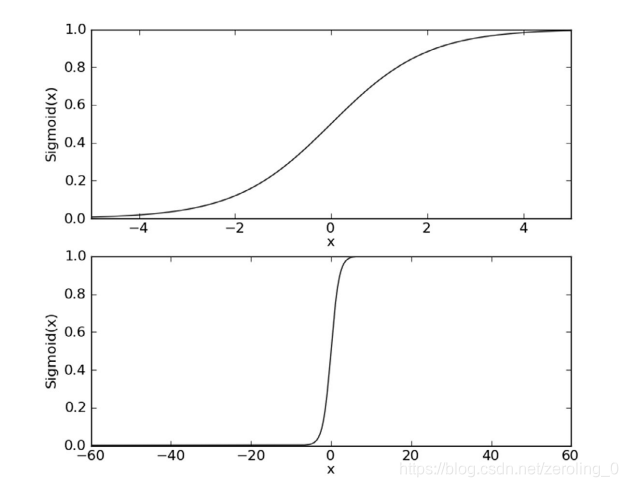
当x=0时，sigmoid函数为0.5，x>0时，sigmoid函数逐渐靠近1，x<0时，sigmoid函数靠近0.输入一个训练数据，得到(0,1)区间的数值，若>0.5，则为1类，<0.5，则为0类。

训练数据若有n个特征（x1,x2,…,xn）

具有线性边界和非线性边界情况分别如下：

现在我们只考虑线性边界情况。

预测函数为：

表示结果取1的概率为，则取0的概率为1-。

2.构建损失函数

预测概率

综合所有训练数据构建函数：

取对数：

越大说明，正确的概率越大。

则越小越好。

3.梯度下降法使的最小/越来越小

则梯度下降可以写成：

α本身为一个常量，因此1/m可以省略。

最终：

梯度上升法最终结果为：

，

可以看出两式最后的结果是相同的。

4.向量化

相关代码如下：

def sigmoid(inX):
    return 1.0/(1+exp(-inX))
def gradAscent(dataMatIn,classLabels):
    dataMarix=mat(dataMatIn)
    labelMat=mat(classLabels).transpose()
    m,n=shape(dataMarix)
    w=ones((n,1))#w=array([1,1,1])
    maxr=500
    alpha=0.001
    for i in range(maxr):
        h=sigmoid(dataMarix*w)
        error=labelMat-h
        w=w+alpha*dataMarix.transpose()*error
    return w