并查集问题比较好理解,种类也不算很多,主要解决的问题为集合分类或者帮派,种族问题 例如在一个城市中有n个人,他们分为不同的帮派,例如a认识b,b认识c那么a,b,c就属于一个帮派我们需要根据给出的关系 算出他们中存在几个帮派 这种类似的题目都可以用并查集来解决 我们用一个数组来记录每一个人属于的集合(帮派)val[n]数组下标表示每一个人的编号而数组总记录的就是这些人所属于的集合 首先我们需要对每一个人进行初始化val[i]=i,即每一个人一开始都是一个集合
void int_set()
{
for(int i=1;i<=n;i++)
{
val[i]=i;
}
}
之后我们需要一个find函数找到每一个元素属于的集合,但是例如val[1]=2;val[2]=3;那么元素1就属于集合2而集合2属于集合3所以1属于集合3为了压缩路径我们可以在寻找的过程中对其进行更新
void int_find(int x)
{
return x==val[x]?x:(int_find(val[x])//val记录的是每一个元素属于的集合而它所属于的集合可能也属于另一个集合所以更新val[x]可以压缩路径实现优化
}
再来我们就需要一个union函数实现两个集合的融合(合并)
void int_union(int x,inty)
{
x=int_find(x);
y=int_find(y);//找到x和y的集合
if(x!=y);
val[x]=val[y];
}
这样利用这三个函数我们就能实现基础的并查集了下面给出例题和模板代码
hdu 1213“How Many Tables”
有n个人一起吃饭,有些人互相认识。认识的人想坐在一起,不想跟陌生人坐。例如A认识B,B认识C,那么A、B、C会坐在一张桌子上。
给出认识的人,问需要多少张桌子。
思路:我们可以认为坐在一张桌子上的就是一个集合,那么多少张桌子就是多少个集合 首先我们根据给出的朋友关系进行元素合并然后遍历每一个val 如果val[i]==i那么就是一个集合而i就是集合的根结点模板代码如下
#include<bits/stdc++.h>
using namespace std;
const int maxed=1000;
int s[maxed],high[maxed];//high表示每一个集合的深度每一次合并时让深度小的并到深度大的上面去可以实现时间复杂度的优化
void int_set()
{
for(int i=1;i<=maxed;i++)
{
s[i]=i;
high[i]=0;
}
}
int int_find(int x)
{
if(x==s[x])
return x;
else
{
s[x]=int_find(s[x]);
}
}
void int_union(int x,int y)
{
x=int_find(x);
y=int_find(y);
if(x!=y)
{
if(high[x]==high[y])
{
s[x]=s[y];
high[y]+1;
}
else
{
if(high[x]>high[y])
s[y]=s[x];
else
s[x]=s[y];
}
}
}
int main()
{
int n,m;
cin>>n>>m;
int_set();
int x,y;
for(int i=0;i<m;i++)
{
cin>>x>>y;
int_union(x,y);
}
int ans=0;
for(int i=1;i<=n;i++)
{
if(i==s[i])
ans++;
}
cout<<ans;
}
当然这只是基础的并查集有些并查集会在这个基础上增加操作 如经典的种族并查集 例题就是poj上的食物链了
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B, B吃C,C吃A。
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是"1 X Y",表示X和Y是同类。
第二种说法是"2 X Y",表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N(1 <= N <= 50,000)和K句话(0 <= K <= 100,000),输出假话的总数。
Input
第一行是两个整数N和K,以一个空格分隔。
以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。
若D=1,则表示X和Y是同类。
若D=2,则表示X吃Y。
Output
只有一个整数,表示假话的数
那么在这种题目种我们需要另外添两个数组总共三个数组 A,B,C
A[i]表示吃B[i]的动物,B[i]表示吃C[i]动物,C[i]表示吃A[i]的动物
那么如果是1吃2那么A[1]就应该和B[2]是一个集合B[1] 就应该和C[2]一个集合C[1]就应该和A[2]一个集合(因A[1]吃A[2],B[2]也吃A[2]那么就是一个集合以此类推)
如果1和2同集合那么A[1]和A[2],B[1]和B[2],C[1]和C[2]分别同一集合如此一来就清晰很多了
那么下面为了方便数组开3*n的大小0~n-1为A n~2*n-1为B 2n~3*n-1为C
完整代码如下
#include<iostream>
#include<cstdio>
using namespace std;
int val[150101];
//因为有a,b,c三种物种所以我们开三倍的n空间 设x为A中的一个动物 那么x+n为B x+2*n为c即x+n吃x x+2*n吃x+n同时也被x吃
int int_find(int x)
{
return x==val[x]?x:(int_find(val[x]));
}
void int_union(int x,int y)
{
x=int_find(x);
y=int_find(y);
if(x!=y)
{
val[x]=val[y];
}
}
bool judge(int x,int y)
{
if(int_find(x)==int_find(y))
return true;
return false;
}
int main()
{
int k,n;
scanf("%d%d",&n,&k);
for(int i=0;i<3*n;i++)
val[i]=i;
int ans=0;
for(int i=0;i<k;i++)
{
int d,x,y;
scanf("%d%d%d",&d,&x,&y);
x--;
y--;
if(x<0||x>=n||y<0||y>=n)
{
ans++;
continue;
}
if(d==1)
{
if(judge(x,y+n)||judge(x,y+2*n))//判断x是否和吃y的是一个种类,x是否和吃吃y的是一个种类
ans++;
else
{
int_union(x,y);
int_union(x+n,y+n);
int_union(x+2*n,y+2*n);
//因为x和y是同类那么吃x和吃y的一定也是同类 被x吃的和被y吃的也是同类由此可讲他们两两结合
}
}
if(d==2)
{
if(judge(x,y)||judge(x,y+2*n))//d=2说明x吃y那么x要和y+n同类不能和y同类也不能和y+2n同类
ans++;
else
{
int_union(x,y+n);
int_union(x+n,y+2*n);
int_union(x+2*n,y);
//因为x和y+n同类那么吃x的一定和吃y+n的同类被x吃的一定和被y+n吃的同类
}
}
}
printf("%d\n",ans);
}
继续深入我发现并查集有时候形成的集合元素之间的关系像树,有时候形成的关系像图
如poj is it a tree 就是一个很典型的树
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
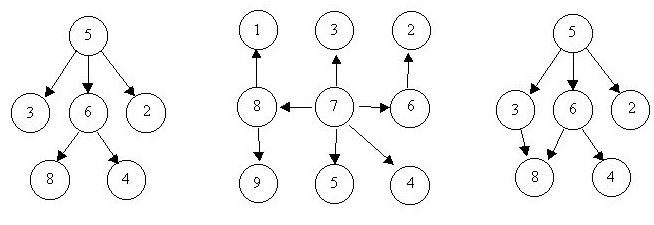
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line "Case k is a tree." or the line "Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).
大概意思就是说给定一些元素的关系如果可以形成一颗树就输出 Case k is a tree否则输出Case k is not a tree
那么我们通过了解树的关系可知树中是一定不可以存在一个封闭的环的那么就是说如果x,y已经属于一个树上了 而题目又给出他们的父子关系那么一定不可能形成一个树了 因为会出现封闭的环
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;//根据树的定义我们可以知道每一个结点(除根节点)有且只有一个父节点可以有多个子节点也就是说一个结点只能做唯一一个结点的子节点
const int maxed=99999;
int val[maxed];
int high[maxed];
int int_find(int x)
{
return x==val[x]?x:(val[x]=int_find(val[x]));
}
void int_union(int x,int y)
{
x=int_find(x);
y=int_find(y);
if(x!=y)
{
if(high[x]<=high[y])
val[x]=val[y];
else
val[y]=val[x];
}
if(high[x]==high[y])
high[y]++;
}
bool judge(int x,int y)
{
return(int_find(x)==int_find(y));
}
int main()
{
int m,n,numb=1;
bool visited[maxed];//visited记录是否被提及到这个结点因为结点的值不确定
while(1)
{
int huan=0;
memset(visited,false,sizeof(visited));
for(int i=0;i<maxed;i++)
{
val[i]=i;
high[i]=0;
}
while(cin>>n>>m)
{
if(n==-1&&m==-1)return 0;
if(n==0&&m==0)break;
visited[n]=visited[m]=true;
if(!judge(n,m))
int_union(n,m);
else
huan=1;
}
int sum=0;
for(int i=1;i<maxed;i++)if(visited[i])
{
if(i==val[i])sum++;
}
if(huan||sum>1)
printf("Case %d is not a tree.\n",numb);
else
printf("Case %d is a tree.\n",numb);
numb++;
}
}
树的题目都有了当然不能少了图,图相较于树我认为就是每一个结点的入度可以为n而树的结点入度为1 根结点的入度为0
下面是图类的例题
一个国家有N个公民,标记为0,1,2,...,N-1,每个公民有一个存款额。已知每个公民有一些朋友,同时国家有一条规定朋友间的存款额之差不能大于d。也就是说,a和b是朋友的话,a有x元的存款,b有y元,那么|x-y|<=d。给定d值与N个人的朋友关系,求这个国家最富有的人和最贫穷的人的存款相差最大的可能值是多少?即求贫富差距的最大值的下界。若这个值为无穷大,输出-1.
Input
多组测试数据,第一行一个整数T,表示测试数据数量,1<=T<=5 每组测试数据有相同的结构构成。 每组数据的第一行两个整数N,d,表示人数与朋友间存款差的最大值,其中2<=N<=50,0<=d<=1000. 接下来有一个N*N的数组A,若A[i][j]='Y'表示i与j两个人是朋友,否则A[i][j]='N'表示不是朋友。其中A[i][i]='N',且保证 A[i][j]=A[j][i].
Output
每组数据一行输出,即这个国家的贫富差距最大值的下界,如果这个值为无穷大输出-1.
因为一个人可以和多个人为朋友所以存在一个结点存在很多入度而此题目无穷大的条件就是存在两个或多个集合(a认识b,b认识c那么这三者就是一个集合)而计算最大贫富差距我们需要从一个人的一个朋友不断向一定方向寻找然后记录人数 人数最多的就是最大的贫富差距例如 a认识b,a认识c,b认识d,d认识e那么从a开始入手有两个方向a->b or a->c那么从a可以写成两个链a->b->d->e and a->c 从b只有一个链b->d->e c入手无链比较之后就可以找到最大的链长那么最大贫富差距从此种产生 代码如下
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define inf 0x3f3f3f
int tree[1005][1005];//记录两人是否为朋友关系是0f3f3f3f是一个很大很大的数
int val[1005];
int int_find(int x)
{
return x==val[x]?x:(val[x]=int_find(val[x]));
}
void int_union(int x,int y)
{
x=int_find(x);
y=int_find(y);
val[x]=val[y];
}
void int_set(int n)
{
for(int i=1;i<=n;i++)
val[i]=i;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int n,d;
char c;
cin>>n>>d;
int_set(n);
memset(tree,inf,sizeof(tree));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>c;
if(c=='Y')
{
tree[i][j]=1;
int_union(i,j);
}
}
tree[i][i]=0;
}
int sum=0;//判断这个集合有几个 若有两个或以上就会无穷大
for(int i=1;i<=n;i++)
{
if(i==int_find(i))//原本写的是i==val[i]但是好像不严谨
sum++;
}
if(sum>1)
printf("-1\n");
else
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
for(int k=1;k<=n;k++)
{
if(tree[j][k]>tree[j][i]+tree[i][k])
tree[j][k]=tree[j][i]+tree[i][k];//如果三人其中j和i是朋友i和k是朋友那么三人的身价形成一个等差数列记录这个数列长
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
ans=max(ans,tree[i][j]);
}
}
cout<<ans*d<<endl;
}
}
}




















 682
682










