1 简介
本文主要根据1988年《Orthogonal least squares methods and their application to non-linear system identification》文中信息提取总结的。
原论文像是一篇综合描述性论文,描述正交最小二乘法及其相关应用,有不少算法细节。
正交最小二乘法用来解决NARMAX模型(non-linear autoregressive moving average with exogenous inputs)的求解。NARMAX是1985年由leontaritis和billings提出的。NARMAX的求解,一是需要确定最终表达式(即模型结构)到底有哪些项(term),比如哪些一次项,哪些二次项,及各种组合;二是就是求解这些项的系数了。
正交的方法可以将模型结构求解和参数求解结合在一起。
2 非线性系统-NARMAX
首先NARMAX的表达式如下,有m个输出y,r个输入u:
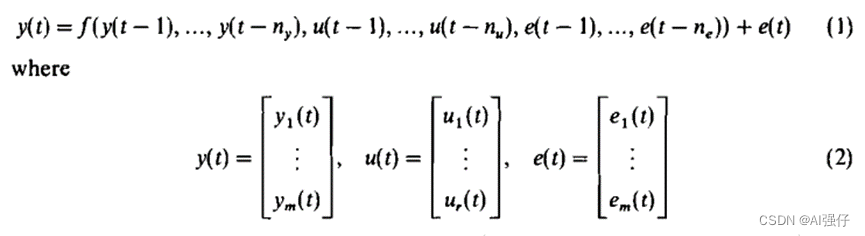
对于其中一个输出y,有下式:
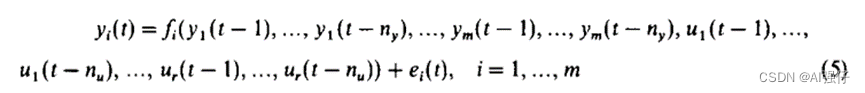
进而可以写成如下形式,反正y就是由各种不同次元的项组成:
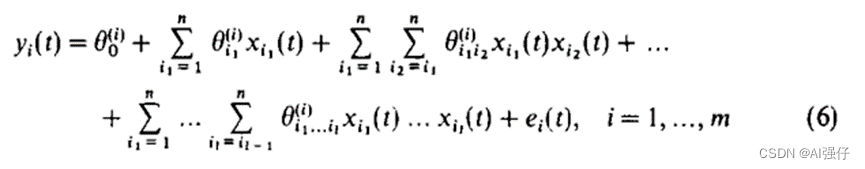
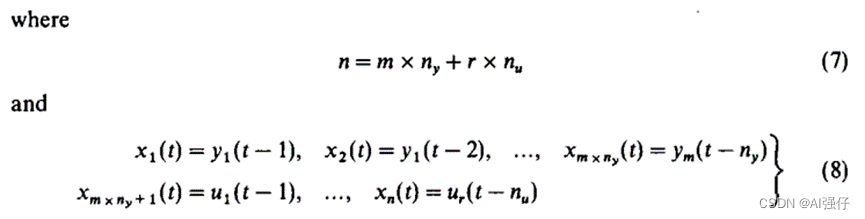
接着写成下式,下面的小写p就可以看成上面不同x的组合,
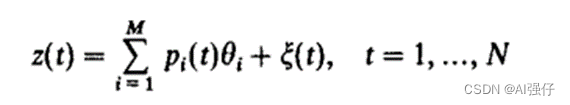
最后写成如下形式:
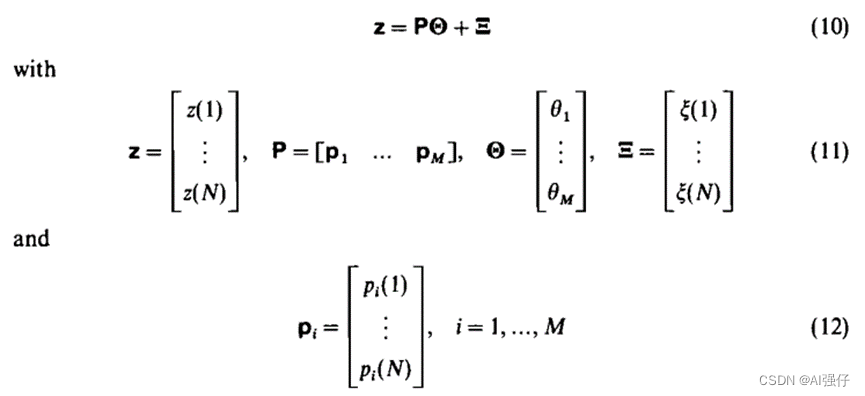
3 最小二乘法
求解上面公式10模型参数θ,就是最小化下面公式:

这个的求解结果满足下面等式,后续章节的各种最小二乘法就是针对该式进行:

4 最小二乘法的不同方法
为了计算模型参数θ,有下面3种方法:
1) 求解上面式13,通过高斯消元(gaussian elimination),或者通过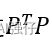 的乔莱斯基分解法;
的乔莱斯基分解法;
2) 构建一个P的正交分解;这种方法就是我们讨论的正交最小二乘法。包括classical Gram-Schmidt正交(格拉姆-施密特正交)、modified Gram-Schmidt正交、householder 转换(豪斯霍尔德变换)、或者Givens 方法(吉文斯法)等这几种求解。其中modified Gram-Schmidt和householder 转换比其他算法更具竞争力,modified Gram-Schmidt容易编程,但计算量稍微大些,比householder 转换稍微更准确些。
3) 构建一个P的奇异值分解(SVD)。计算成本较高。
5 P子集的选择
当识别一个非线性系统,其结构未知,要避免损失掉重要的项(term),但也不能导致项很多、次元很高。就涉及P的子集的选择。文中对classical Gram-Schmidt正交、modified Gram-Schmidt正交、householder 转换怎么进行子集选择进行了描述。
6 实验结果
下面是采用householder 转换求解NARMAX。
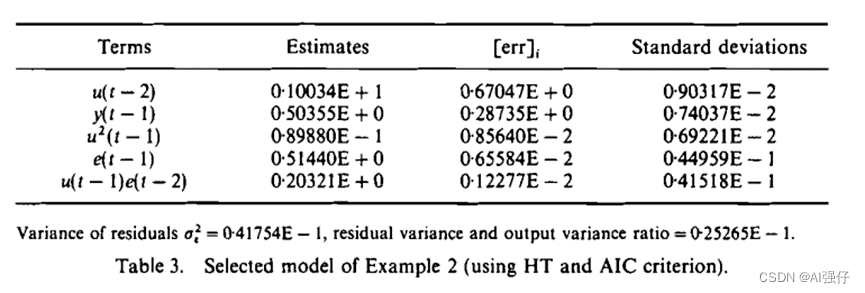





 本文介绍了正交最小二乘法在解决非线性系统NARMAX模型求解中的作用,详细阐述了NARMAX模型的结构和求解过程。最小二乘法的三种计算方法被提出,包括高斯消元、正交分解(如modifiedGram-Schmidt和Householder变换)以及奇异值分解,其中Householder变换在实验中得到应用。文章还讨论了如何选择P子集以优化模型复杂性和准确性。
本文介绍了正交最小二乘法在解决非线性系统NARMAX模型求解中的作用,详细阐述了NARMAX模型的结构和求解过程。最小二乘法的三种计算方法被提出,包括高斯消元、正交分解(如modifiedGram-Schmidt和Householder变换)以及奇异值分解,其中Householder变换在实验中得到应用。文章还讨论了如何选择P子集以优化模型复杂性和准确性。
















 4272
4272

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








