PyTorch实现神经网络的误差反向传播

一、误差反向传播介绍

误差反向传播（Backpropagation，简称 BP）是一种用于训练人工神经网络的算法，其核心思想是基于梯度下降策略，利用损失函数（如均方误差、交叉熵损失等）计算网络输出与真实标签之间的误差，然后将误差从输出层反向传播到输入层，通过链式法则计算每个神经元参数（权重和偏置）对误差的梯度，进而更新这些参数，以减少网络预测结果与真实结果之间的误差，使得网络的预测能力不断提升。

具体来说，在神经网络前向传播过程中，输入数据经过层层神经元的计算得到输出结果，之后根据输出结果与真实标签计算出误差。反向传播时，从输出层开始，将误差按照一定规则分配到每一层的神经元，计算每个神经元的参数对误差的影响程度（即梯度），最后使用优化算法（如随机梯度下降）根据梯度对参数进行更新，不断迭代这个过程，直到网络达到满意的性能。
 

误差反向传播的特点：
【1】高效计算梯度
传统的直接计算梯度方法，对于大型神经网络，计算量会随着网络规模呈指数级增长。而误差反向传播利用链式法则，巧妙地将梯度计算过程转化为一系列相对简单的局部计算，大大减少了计算量。例如，在一个具有数百万参数的深度神经网络中，使用误差反向传播算法，能在可接受的时间内完成梯度计算，使得大规模网络的训练成为可能。
【2】适合复杂模型训练
神经网络能够学习复杂的非线性映射关系，而误差反向传播算法可以适应这种复杂结构。它通过不断调整各层神经元之间的连接权重和偏置，使网络能够拟合复杂的数据分布。无论是处理图像、语音等非结构化数据，还是解决复杂的回归、分类问题，误差反向传播都能有效地训练网络，挖掘数据中的复杂模式。
【3】易陷入局部最优
由于误差反向传播基于梯度下降，在优化过程中，网络可能会陷入局部最优解。也就是说，找到的参数组合虽然在局部区域内使误差最小，但并非全局最小。例如，在一个复杂的损失函数曲面中，可能存在许多 “山谷”，梯度下降算法可能只是找到了其中一个较浅的 “山谷”，而错过了全局最优的更深 “山谷”。不过，通过改进优化算法（如使用动量法、Adagrad 等）、调整学习率等方法，可以在一定程度上缓解这个问题。
【4】依赖大量数据
为了准确计算梯度并找到较好的参数组合，误差反向传播通常需要大量的训练数据。数据量不足时，计算出的梯度可能不准确，导致网络难以学习到有效的特征和规律，容易出现过拟合现象，即网络在训练数据上表现良好，但在测试数据上表现不佳。

二、误差反向传播的案例

【1】手写数字识别
在手写数字识别任务中，需要构建一个神经网络，让它能够识别出 0 - 9 这十个手写数字。首先，收集大量的手写数字图片及其对应的真实标签作为训练数据。在训练阶段，将手写数字图片数据输入到神经网络进行前向传播，得到网络的预测结果，比如网络预测某个手写数字图片对应的数字是 “5”，但真实标签是 “3”，此时就产生了误差。接着，通过误差反向传播算法，将这个误差从输出层反向传播到网络的每一层，计算出每个神经元的权重和偏置对误差的梯度，然后根据梯度调整这些参数。经过大量数据的反复训练，不断优化网络参数，使得网络能够准确识别手写数字。当遇到新的手写数字图片时，训练好的网络就能给出较为准确的预测结果，广泛应用于邮政信件分拣、银行支票数字识别等场景。

【2】推荐系统
电商平台或视频网站等常常使用推荐系统，根据用户的历史行为（如购买记录、浏览记录等）为用户推荐商品或视频。可以将用户的行为数据作为输入，经过神经网络的前向传播，输出用户对不同商品或视频的感兴趣程度预测值。如果预测用户对某商品感兴趣，但实际用户并未购买或点击，就产生了误差。利用误差反向传播算法，将误差反向传播，更新网络参数，使网络能够更好地学习用户行为与兴趣之间的关系。随着不断训练，推荐系统能够更精准地为用户推荐他们可能感兴趣的内容，提高用户的购物体验或观看时长，增加平台的用户粘性和商业价值 。
以上从原理、特点和应用场景介绍了误差反向传播。若你还想了解其与其他算法对比，或对案例有更深入探讨，欢迎随时交流。

三、多层感知机误差反向传播过程

1、模型假定

2、前向传播过程

3、计算误差

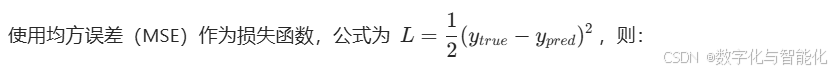
4、反向传播过程

5、参数更新​

假设学习率 η=0.1，根据梯