题1
根据书中对傅立叶变换的定义,证明傅立叶变换的平移性质
f
(
x
,
y
)
e
j
2
π
(
u
0
x
/
M
+
v
0
y
/
N
)
⇔
F
(
u
−
u
0
,
v
−
v
0
)
f\left( {x,y} \right){e^{j2\pi \left( {{u_0}x/M + {v_0}y/N} \right)}} \Leftrightarrow F\left( {u - {u_0},v - {v_0}} \right)
f(x,y)ej2π(u0x/M+v0y/N)⇔F(u−u0,v−v0)
f
(
x
−
x
0
,
y
−
y
0
)
⇔
F
(
u
,
v
)
e
−
j
2
π
(
x
0
u
/
M
+
y
0
v
/
N
)
f\left( {x - {x_0},y - {y_0}} \right) \Leftrightarrow F\left( {u,v} \right){e^{ - j2\pi \left( {{x_0}u/M + {y_0}v/N} \right)}}
f(x−x0,y−y0)⇔F(u,v)e−j2π(x0u/M+y0v/N)
证:
先证
f
(
x
,
y
)
e
j
2
π
(
u
0
x
/
M
+
v
0
y
/
N
)
⇔
F
(
u
−
u
0
,
v
−
v
0
)
f\left( {x,y} \right){e^{j2\pi \left( {{u_0}x/M + {v_0}y/N} \right)}} \Leftrightarrow F\left( {u - {u_0},v - {v_0}} \right)
f(x,y)ej2π(u0x/M+v0y/N)⇔F(u−u0,v−v0)
对左式做离散傅里叶变换:
D
F
T
(
f
(
x
,
y
)
e
j
2
π
(
u
0
x
/
M
+
v
0
y
/
N
)
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
(
f
(
x
,
y
)
e
j
2
π
(
u
0
x
/
M
+
v
0
y
/
N
)
)
e
−
j
2
π
(
u
x
/
M
,
v
y
/
N
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
j
2
π
(
u
0
x
/
M
+
v
0
y
/
N
)
−
j
2
π
(
u
x
/
M
,
v
y
/
N
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
−
j
2
π
(
u
−
u
0
M
x
+
v
−
v
0
N
)
=
F
(
u
−
u
0
,
v
−
v
0
)
\begin{array}{l} DFT\left( {f\left( {x,y} \right){e^{j2\pi \left( {{u_0}x/M + {v_0}y/N} \right)}}} \right)\\ \;\; = \sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{N - 1} {\left( {f\left( {x,y} \right){e^{j2\pi \left( {{u_0}x/M + {v_0}y/N} \right)}}} \right){e^{ - j2\pi \left( {ux/M,vy/N} \right)}}} } \\ \;\; = \sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{N - 1} {f\left( {x,y} \right){e^{j2\pi \left( {{u_0}x/M + {v_0}y/N} \right) - j2\pi \left( {ux/M,vy/N} \right)}}} } \\ \;\; = \sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{N - 1} {f\left( {x,y} \right){e^{ - j2\pi \left( {\frac{{u - {u_0}}}{M}x + \frac{{v - {v_0}}}{N}} \right)}}} } \\ \;\; = F\left( {u - {u_0},v - {v_0}} \right) \end{array}
DFT(f(x,y)ej2π(u0x/M+v0y/N))=x=0∑M−1y=0∑N−1(f(x,y)ej2π(u0x/M+v0y/N))e−j2π(ux/M,vy/N)=x=0∑M−1y=0∑N−1f(x,y)ej2π(u0x/M+v0y/N)−j2π(ux/M,vy/N)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mu−u0x+Nv−v0)=F(u−u0,v−v0)
得证
再证明性质
f
(
x
−
x
0
,
y
−
y
0
)
⇔
F
(
u
,
v
)
e
−
j
2
π
(
x
0
u
/
M
+
y
0
v
/
N
)
f\left( {x - {x_0},y - {y_0}} \right) \Leftrightarrow F\left( {u,v} \right){e^{ - j2\pi \left( {{x_0}u/M + {y_0}v/N} \right)}}
f(x−x0,y−y0)⇔F(u,v)e−j2π(x0u/M+y0v/N)
对右式做离散逆傅里叶变换:
I
D
E
T
(
F
(
u
,
v
)
e
−
j
2
π
(
x
0
u
/
M
+
y
0
v
/
N
)
)
=
1
M
N
∑
u
=
0
M
−
1
∑
v
=
0
N
−
1
(
F
(
u
,
v
)
e
−
j
2
π
(
x
0
u
/
M
+
y
0
v
/
N
)
)
e
j
2
π
(
u
x
/
M
+
v
y
/
N
)
=
1
M
N
∑
u
=
0
M
−
1
∑
v
=
0
N
−
1
F
(
u
,
v
)
e
−
j
2
π
(
x
0
u
/
M
+
y
0
v
/
N
)
+
j
2
π
(
u
x
/
M
+
v
y
/
N
)
=
1
M
N
∑
u
=
0
M
−
1
∑
v
=
0
N
−
1
F
(
u
,
v
)
e
j
2
π
(
x
−
x
0
M
u
+
y
−
y
0
N
v
)
=
f
(
x
−
x
0
,
y
−
y
0
)
\begin{array}{l} IDET\left( {F\left( {u,v} \right){e^{ - j2\pi \left( {{x_0}u/M + {y_0}v/N} \right)}}} \right)\\ \;\;\; = \frac{1}{{MN}}\sum\limits_{u = 0}^{M - 1} {\sum\limits_{v = 0}^{N - 1} {\left( {F\left( {u,v} \right){e^{ - j2\pi \left( {{x_0}u/M + {y_0}v/N} \right)}}} \right)} } {e^{j2\pi \left( {ux/M + vy/N} \right)}}\\ \;\;\; = \frac{1}{{MN}}\sum\limits_{u = 0}^{M - 1} {\sum\limits_{v = 0}^{N - 1} {F\left( {u,v} \right){e^{ - j2\pi \left( {{x_0}u/M + {y_0}v/N} \right) + j2\pi \left( {ux/M + vy/N} \right)}}} } \\ \;\;\; = \frac{1}{{MN}}\sum\limits_{u = 0}^{M - 1} {\sum\limits_{v = 0}^{N - 1} {F\left( {u,v} \right){e^{j2\pi \left( {\frac{{x - {x_0}}}{M}u + \frac{{y - {y_0}}}{N}v} \right)}}} } \\ \;\;\; = f\left( {x - {x_0},y - {y_0}} \right) \end{array}
IDET(F(u,v)e−j2π(x0u/M+y0v/N))=MN1u=0∑M−1v=0∑N−1(F(u,v)e−j2π(x0u/M+y0v/N))ej2π(ux/M+vy/N)=MN1u=0∑M−1v=0∑N−1F(u,v)e−j2π(x0u/M+y0v/N)+j2π(ux/M+vy/N)=MN1u=0∑M−1v=0∑N−1F(u,v)ej2π(Mx−x0u+Ny−y0v)=f(x−x0,y−y0)
得证
习题2
观察如下所示图像。右边的图像这样得到:(a)在原始图像左边乘以
(
−
1
)
x
+
y
\left(-1\right)^{x+y}
(−1)x+y;(b) 计算离散傅里叶变换(DFT); (c) 对变换取复共轭; (d) 计算傅里叶反变换; (d) 结果的实部再乘以E
(
−
1
)
x
+
y
\left(-1\right)^{x+y}
(−1)x+y。(用数学方法解释为什么会产生右图的效果。)

答:
设原图像为
f
(
x
,
y
)
f\left( {x,y} \right)
f(x,y)
步骤(a):
f
a
(
x
,
y
)
=
(
−
1
)
x
+
y
f
(
x
,
y
)
{f_a}\left( {x,y} \right) = {\left( { - 1} \right)^{x + y}}f\left( {x,y} \right)
fa(x,y)=(−1)x+yf(x,y)
步骤(b):由傅里叶变换的平移性质得
D
F
T
(
f
a
(
x
,
y
)
)
=
F
(
u
−
M
2
,
v
−
N
2
)
DFT\left( {{f_a}\left( {x,y} \right)} \right) = F\left( {u - \frac{M}{2},v - \frac{N}{2}} \right)
DFT(fa(x,y))=F(u−2M,v−2N)
步骤(c):由傅里叶变换的共轭对称性质得
F
∗
(
u
−
M
2
,
v
−
N
2
)
=
F
(
−
(
u
−
M
2
)
,
−
(
v
−
N
2
)
)
{F^*}\left( {u - \frac{M}{2},v - \frac{N}{2}} \right) = F\left( { - \left( {u - \frac{M}{2}} \right), - \left( {v - \frac{N}{2}} \right)} \right)
F∗(u−2M,v−2N)=F(−(u−2M),−(v−2N))
步骤(d):由傅里叶的伸缩性质
f
(
a
x
)
⇔
1
∣
a
∣
F
(
u
a
)
f\left( {ax} \right) \Leftrightarrow \frac{1}{{\left| a \right|}}F\left( {\frac{u}{a}} \right)
f(ax)⇔∣a∣1F(au)结合步骤(a)得
I
D
F
T
(
F
(
−
(
u
−
M
2
)
,
−
(
v
−
N
2
)
)
)
=
(
−
1
)
−
(
x
+
y
)
f
(
−
x
,
−
y
)
IDFT\left( {F\left( { - \left( {u - \frac{M}{2}} \right), - \left( {v - \frac{N}{2}} \right)} \right)} \right) = {\left( { - 1} \right)^{ - \left( {x + y} \right)}}f\left( { - x, - y} \right)
IDFT(F(−(u−2M),−(v−2N)))=(−1)−(x+y)f(−x,−y)
步骤(e):
(
−
1
)
−
(
x
+
y
)
(
−
1
)
x
+
y
f
(
−
x
,
−
y
)
=
f
(
−
x
,
−
y
)
{\left( { - 1} \right)^{ - \left( {x + y} \right)}}{\left( { - 1} \right)^{x + y}}f\left( { - x, - y} \right) = f\left( { - x, - y} \right)
(−1)−(x+y)(−1)x+yf(−x,−y)=f(−x,−y)
因此图像最后旋转
习题3
高斯型低通滤波器在频域中的传递函数是
H
(
u
,
v
)
=
A
e
−
(
u
2
+
v
2
)
2
σ
2
H\left(u,v\right)=Ae^{-{(u^2+v^2)}{2\sigma^2}}
H(u,v)=Ae−(u2+v2)2σ2根据二维傅里叶性质,证明空间域的相应滤波器形式为
h
(
x
,
y
)
=
A
2
π
σ
2
e
−
2
π
2
σ
2
(
x
2
+
y
2
)
h\left(x,y\right)=A2\pi\sigma^2e^{-2\pi^2\sigma^2(x^2+y^2)}
h(x,y)=A2πσ2e−2π2σ2(x2+y2)(这些闭合形式只适用于连续变量情况。)
在证明中假设已经知道如下结论:函数
e
−
π
(
x
2
+
y
2
)
e^{-\pi(x^2+y^2)}
e−π(x2+y2)的傅立叶变换为
e
−
π
(
u
2
+
v
2
)
e^{-\pi(u^2+v^2)}
e−π(u2+v2)
证:
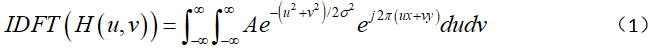
令
u
=
2
π
σ
U
u = \sqrt {2\pi } \sigma U
u=2πσU,
v
=
2
π
σ
V
v = \sqrt {2\pi } \sigma V
v=2πσV,则上式变为(2)
I
D
F
T
(
H
(
u
,
v
)
)
=
A
2
π
σ
2
∫
−
∞
∞
∫
−
∞
∞
e
−
π
(
U
2
+
V
2
)
e
j
2
π
(
2
π
σ
U
x
+
2
π
σ
V
y
)
d
U
d
V
IDFT\left( {H\left( {u,v} \right)} \right) = A2\pi {\sigma ^2}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{e^{ - \pi \left( {{U^2} + {V^2}} \right)}}{e^{j2\pi \left( {\sqrt {2\pi } \sigma Ux + \sqrt {2\pi } \sigma Vy} \right)}}dUdV} }
IDFT(H(u,v))=A2πσ2∫−∞∞∫−∞∞e−π(U2+V2)ej2π(2πσUx+2πσVy)dUdV
根据题目给出得结论:函数
e
−
π
(
x
2
+
y
2
)
e^{-\pi(x^2+y^2)}
e−π(x2+y2)的傅立叶变换为
e
−
π
(
u
2
+
v
2
)
e^{-\pi(u^2+v^2)}
e−π(u2+v2),得到(3):
e
−
π
(
x
2
+
y
2
)
=
∫
−
∞
∞
∫
−
∞
∞
e
−
π
(
u
2
+
v
2
)
e
j
2
π
(
u
x
+
v
y
)
d
u
d
v
{e^{ - \pi \left( {{x^2} + {y^2}} \right)}} = \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{e^{ - \pi \left( {{u^2} + {v^2}} \right)}}{e^{j2\pi \left( {ux + vy} \right)}}dudv} }
e−π(x2+y2)=∫−∞∞∫−∞∞e−π(u2+v2)ej2π(ux+vy)dudv
令
x
=
2
π
σ
X
x = \sqrt {2\pi } \sigma X
x=2πσX,
y
=
2
π
σ
Y
y = \sqrt {2\pi } \sigma Y
y=2πσY,等式两边再乘以
A
2
π
σ
2
A2\pi {\sigma ^2}
A2πσ2 ,则上式变为
A
2
π
σ
2
e
−
2
π
2
σ
2
(
X
2
+
Y
2
)
=
A
2
π
σ
2
∫
−
∞
∞
∫
−
∞
∞
e
−
π
(
u
2
+
v
2
)
e
j
2
π
(
2
π
σ
u
X
+
2
π
σ
v
Y
)
d
u
d
v
A2\pi {\sigma ^2}{e^{ - 2{\pi ^2}{\sigma ^2}\left( {{X^2} + {Y^2}} \right)}} = A2\pi {\sigma ^2}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{e^{ - \pi \left( {{u^2} + {v^2}} \right)}}{e^{j2\pi \left( {\sqrt {2\pi } \sigma uX + \sqrt {2\pi } \sigma vY} \right)}}dudv} }
A2πσ2e−2π2σ2(X2+Y2)=A2πσ2∫−∞∞∫−∞∞e−π(u2+v2)ej2π(2πσuX+2πσvY)dudv
对比式(2)和式(4)得:
I
D
F
T
(
H
(
u
,
v
)
)
=
A
2
π
σ
2
e
−
2
π
2
σ
2
(
X
2
+
Y
2
)
IDFT\left( {H\left( {u,v} \right)} \right) = A2\pi {\sigma ^2}{e^{ - 2{\pi ^2}{\sigma ^2}\left( {{X^2} + {Y^2}} \right)}}
IDFT(H(u,v))=A2πσ2e−2π2σ2(X2+Y2)得证
习题4

答:没有区别。对图像补零是为了使直接卷积公式法和DFT方法产生得卷积结果相同,后者必须对函数周期补足。考虑到傅里叶变换的周期性,如果将左边的图像以覆盖整个平面的方式复制多次,将形成一个棋盘,棋盘中每个方格都是本图片和黑色的扩展部分。如果将右边的图片做同样的处理,也得到相同的结果。

习题5
请证明第二版课本习题4.5中提及的频域内高通滤波器与低通滤波器的关系式子。

答:可以认为原始图像由高频部分和低频部分组成:
f
(
x
,
y
)
=
f
r
(
x
,
y
)
+
f
p
(
x
,
y
)
f\left( {x,y} \right) = {f_r}\left( {x,y} \right) + {f_p}\left( {x,y} \right)
f(x,y)=fr(x,y)+fp(x,y)
而高频部分和低频部分可以由原图像作卷积得到,即:
f
(
x
,
y
)
=
f
(
x
,
y
)
∗
h
b
r
(
x
,
y
)
+
f
(
x
,
y
)
∗
h
b
p
(
x
,
y
)
f\left( {x,y} \right) = f\left( {x,y} \right)*{h_{br}}\left( {x,y} \right) + f\left( {x,y} \right)*{h_{bp}}\left( {x,y} \right)
f(x,y)=f(x,y)∗hbr(x,y)+f(x,y)∗hbp(x,y)
等上式两边分别做傅里叶变换:
F
(
u
,
v
)
=
F
(
u
,
v
)
H
b
r
(
u
,
v
)
+
F
(
u
,
v
)
H
b
p
(
u
,
v
)
F
(
u
,
v
)
=
F
(
u
,
v
)
(
H
b
r
(
u
,
v
)
+
H
b
p
(
u
,
v
)
)
1
=
H
b
r
(
u
,
v
)
+
H
b
p
(
u
,
v
)
H
b
p
(
u
,
v
)
=
1
−
H
b
r
(
u
,
v
)
\begin{array}{l} F\left( {u,v} \right) = F\left( {u,v} \right){H_{br}}\left( {u,v} \right) + F\left( {u,v} \right){H_{bp}}\left( {u,v} \right)\\ F\left( {u,v} \right) = F\left( {u,v} \right)\left( {{H_{br}}\left( {u,v} \right) + {H_{bp}}\left( {u,v} \right)} \right)\\ 1 = {H_{br}}\left( {u,v} \right) + {H_{bp}}\left( {u,v} \right)\\ {H_{bp}}\left( {u,v} \right) = 1 - {H_{br}}\left( {u,v} \right) \end{array}
F(u,v)=F(u,v)Hbr(u,v)+F(u,v)Hbp(u,v)F(u,v)=F(u,v)(Hbr(u,v)+Hbp(u,v))1=Hbr(u,v)+Hbp(u,v)Hbp(u,v)=1−Hbr(u,v)
所以
H
b
p
(
u
,
v
)
=
1
−
H
b
r
(
u
,
v
)
{H_{bp}}\left( {u,v} \right) = 1 - {H_{br}}\left( {u,v} \right)
Hbp(u,v)=1−Hbr(u,v)得证
























 1028
1028

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








