滴水逆向——C++_二叉树_二叉树逆向-优快云博客

本文链接：https://blog.youkuaiyun.com/z17805008775/article/details/105750132

这篇博客详细介绍了二叉树的各种类型，包括满二叉树、完全二叉树、平衡二叉树（如AVL树和红黑树）以及哈夫曼树。文章还探讨了二叉树的基本概念，如根节点、度、深度和高度，并阐述了前序、中序、后序和广度优先等遍历方法。此外，博主深入讲解了二叉搜索树的特性及其增、删、查操作。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、概念：

1.分类：

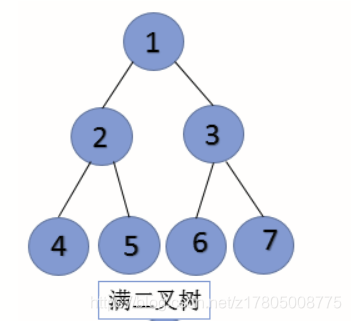
满二叉树:除叶子结点外, 所有结点都有两个结点, 叶子结点的left, right为NULL.
完全二叉树 : 除了最底层的叶子结点之外, 其余层全满, 而且叶子层集中在左端.堆是一种特殊的完全二叉树(全满或者差一个结点就全满)
平衡二叉树：所谓平衡二叉树指的是，左右两个子树的高度差的绝对值不超过 1。包括AVL树, 红黑树.
哈夫曼树：又称为最优二叉数，是一种带权路径最短的树。哈夫曼编码就是哈夫曼树的应用, 可以用来进行编码压缩.哈夫曼树的构造见哈夫曼树的构造
红黑树：具体见红黑树问题

2.关键词：

根节点
父节点
子节点
左子树
右子树
度：结点拥有的子树数目称为结点的度
深度/高度：树中结点的最大层次数

3.遍历：

前序遍历(根左右)：GDAFEMHZ
中序遍历(左根右)：ADEFGHMZ
后序遍历(左右根)：AEFDHZMG
广度优先遍历DFS : GDMAFHZE
深度优先遍历BFS : GDAFEMHZ

4、二叉树遍历：

#include<stdio.h>
#include<Windows.h>

class Monster
{
public:
	int ID;
	int Level;
	char Name[20];
public:
	Monster() {}
	Monster(int ID, int Level, char* Name)
	{
		this->ID = ID;
		this->Level = Level;
		memcpy(&this->Name, Name, strlen(Name) + 1);
	}
};

template<class T>
class TreeNode {
public:
	T element;					//当前节点存储的数据			
	TreeNode<T>* pLeft;					//指向左子节点的指针			
	TreeNode<T>* pRight;					//指向右子节点的指针			

	TreeNode(T& ele) {
		//初始化Node节点							
		memset(&element, 0, sizeof(TreeNode));
		//为元素赋值							
		memcpy(&element, &ele, sizeof(T));
		pLeft = pRight = NULL;
	}
};

template<class T>
class BSortTree {
public:
	BSortTree();					//构造函数			
	~BSortTree();					//析构函数			
public:
	void InOrderTraverse(TreeNode<T>* pNode);					//中序遍历			
	void PreOrderTraverse(TreeNode<T>* pNode);					//前序遍历			
	void PostOrderTraverse(TreeNode<T>* pNode);					//后序遍历			
	TreeNode<T>* GetRoot();					//返回根节点			
	int GetDepth(TreeNode<T>* pNode);					//返回某个节点的高度/深度			
private:
	void Init();
	void Destory(TreeNode<T>* pNode);
private:
	TreeNode<T>* m_pRoot;					//根结点指针			
	int size;					//树中元素总个数			
};

template<class T>
BSortTree<T>::BSortTree()
{
	Init();
}
template<class T>
BSortTree<T>::~BSortTree() 
{
	printf("Destory function...\n");
	Destory(m_pRoot);
}

template<class T>
void BSortTree<T>::Destory(TreeNode<T>* pNode)
{
	//释放所有节点空间		
	if (pNode==NULL)
	{	
		return ;
	}
	else
	{
		Destory(pNode->pLeft);
		Destory(pNode->pRight);
		delete pNode;
		pNode = NULL;
	}
}

template<class T>
void BSortTree<T>::Init()
{

	Monster m1(1, 1, (char*)"刺猬");
	Monster m2(