重点
- 拉格朗日插值可以用来填充缺失的数据,数据清洗中的一步
解决问题
给定NN个点,求取函数f(x)f(x), 满足f(xi)=yif(xi)=yi. 利用这种插值方法,可以填充缺失的数据.
拉格朗日插值对上述问题的给出的解有如下形式:
f(x)=∑Nj=0yifi(x)f(x)=∑j=0Nyifi(x),其中
fi(x)=∏Nj≠ix−xjxi−xjfi(x)=∏j≠iNx−xjxi−xj
拉格朗日插值有如下性质:
fi(x)fi(x)是一个(N−1)(N−1)阶函数
在已知的N个点中
fi(x)=1 if x=xifi(x)=1 if x=xi
fi(x)=0 if x≠xifi(x)=0 if x≠xi根据上面的结果,插值函数f(x)f(x)满足 f(xi)=yif(xi)=yi for i∈[0,N−1]i∈[0,N−1] (这就是插值的目标)
例子
给定三个点(x1,y1),(x2,y2),(x3,y3)(x1,y1),(x2,y2),(x3,y3), 则
f(x)=∑3j=0yifi(x)=y1f1(x)+y2f2(x)+y3f3(x)f(x)=∑j=03yifi(x)=y1f1(x)+y2f2(x)+y3f3(x),其中
f1(x)=x−x2x1−x2×x−x3x1−x3f1(x)=x−x2x1−x2×x−x3x1−x3
f2(x)=x−x1x2−x1×x−x3x2−x3f2(x)=x−x1x2−x1×x−x3x2−x3
f3(x)=x−x1x3−x1×x−x2x3−x2f3(x)=x−x1x3−x1×x−x2x3−x2
代码
scipy.interpolate.lagrange可以完成拉格朗日插值
已知点的数目加一比目标函数的阶数小
from scipy.interpolate import lagrange
import numpy as np
from matplotlib import pyplot as plt
x = np.array([0, 1, 2])
y = x**3
poly = lagrange(x, y)
x = np.arange(-5,5)
y = x ** 3
predy = poly(x)
plt.plot(x,y,label='groundtruth',color='r')
plt.plot(x,predy,label='predicted',color='y')
plt.legend()
plt.show()结果图
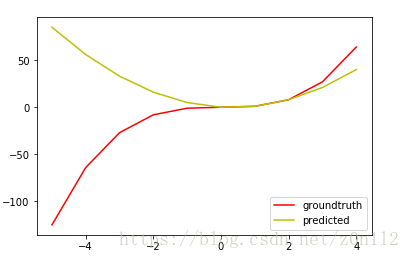
可以看出拟合效果很差,因为目标函数y=x3y=x3是三阶曲线,但只给出3个点,拉格朗日插值只能生成一个二阶曲线,必然无法拟合
已知点的数目加一等于目标函数的阶数
from scipy.interpolate import lagrange
import numpy as np
from matplotlib import pyplot as plt
x = np.array([0, 1, 2,3])
y = x**3
poly = lagrange(x, y)
x = np.arange(-5,5)
y = x ** 3
predy = poly(x)
plt.plot(x,y,label='groundtruth',color='r')
plt.plot(x,predy,label='predicted',color='y')
plt.legend()
plt.show()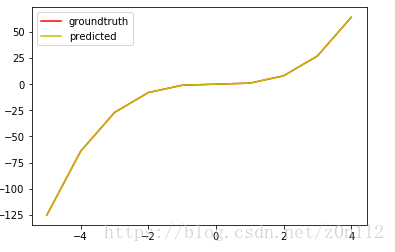
给定四个点就可以完美拟合三阶曲线
已知点的数目加一大于目标函数的阶数
from scipy.interpolate import lagrange
import numpy as np
from matplotlib import pyplot as plt
x = np.array([0, 1, 2,3,4])
y = x**3
poly = lagrange(x, y)
x = np.arange(-5,5)
y = x ** 3
predy = poly(x)
plt.plot(x,y,label='groundtruth',color='r')
plt.plot(x,predy,label='predicted',color='y')
plt.legend()
plt.show()
给定五个点也可以完美拟合三阶曲线
已知点的数目加一大于目标函数的阶数,但存在噪声
from scipy.interpolate import lagrange
import numpy as np
from matplotlib import pyplot as plt
x = np.array([0, 1, 2,3,4])
y = x**3
y[-1] -= 5 #噪声
poly = lagrange(x, y)
x = np.arange(-5,5)
y = x ** 3
predy = poly(x)
plt.plot(x,y,label='groundtruth',color='r')
plt.plot(x,predy,label='predicted',color='y')
plt.legend()
plt.show()
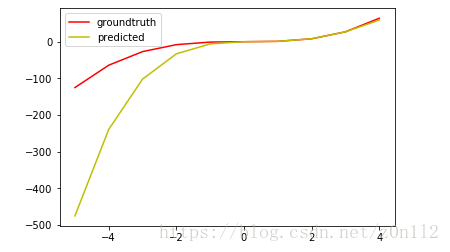
噪声导致拟合误差增大,也是合理的结果





 博客介绍了拉格朗日插值在数据清洗中的应用,它可用于填充缺失数据。给定N个点求取满足特定条件的函数f(x),拉格朗日插值给出了相应解的形式及性质。还通过例子展示其计算方式,并用代码测试不同点数和噪声情况下的拟合效果。
博客介绍了拉格朗日插值在数据清洗中的应用,它可用于填充缺失数据。给定N个点求取满足特定条件的函数f(x),拉格朗日插值给出了相应解的形式及性质。还通过例子展示其计算方式,并用代码测试不同点数和噪声情况下的拟合效果。
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








