相机标定

最新推荐文章于 2024-12-04 22:49:29 发布

z0n1l2

最新推荐文章于 2024-12-04 22:49:29 发布

阅读量672

点赞数

分类专栏： 3D 文章标签：相机标定 3D 张友正标定法

3D 专栏收录该内容

1 篇文章

订阅专栏

本文详细介绍了相机坐标系的几种类型及其之间的变换过程，包括世界坐标系、相机坐标系、像素坐标系和图像坐标系。同时深入探讨了张友正标定法的基本原理与步骤，帮助读者理解如何计算相机的内外参数及畸变系数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

基础知识

几个重要的坐标系

world coordinates
描述我们处于的这个世界的三维直角坐标系,原点和坐标轴的选择有很大自由度
camera coordinates
可以看作是world coordinates的一个具体化,原点定在镜头光心,z轴是光轴,x,y轴构成一个和z轴垂直的面,这个面和后面的成像平面平行

世界坐标系坐标 $(x_w, y_w,z_w)$ 和相机坐标系坐标 $(x_c,y_c,z_c)$ 通过旋转和平移进行转换,矩阵形式如下

$(x c, y c, z c, 1) T = ⎡ ⎣ ⎢ R, T 0, 1 ⎤ ⎦ ⎥ \times (x w, y w, z w, 1) T$ $(x_c,y_c,z_c,1)^T = \begin{bmatrix} R, T \\\\ 0, 1 \end{bmatrix} \times (x_w,y_w,z_w,1)^T$
其中R是旋转矩阵, T是平移矩阵
pixel coordinates
一个二维直角坐标系, x-y轴的单位是CCD或CMOS的成像单元的尺寸
image coordinates
图像处理中最常见的二维直角坐标系, x-y轴单位是像素点个数(这里的像素点和pixel coordinates中的pixel不是一个东西. pixel coordinates里的pixel是物理尺寸, 而此处是逻辑尺寸,逻辑上像素是没有大小的)

像素坐标系 $(X,Y)$ 和图像坐标系 $(u,v)$ 通过缩放和平移进行转换,矩阵形式如下

$(u, v, 1) T = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ 1 / d X, 0, u 0 0, 1 / d Y, v 0 0, 0, 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ \times (X, Y, 1) T$ $(u,v,1)^T = \begin{bmatrix} 1/dX,0, u_0 \\\\ 0,1/dY,v_0 \\\\ 0,0,1 \end{bmatrix} \times (X,Y,1)^T$
其中 $1/dX$ 和 $1/dY$ 是成像单元在x和y轴上的物理尺寸
小孔成像
截至目前,已知以下两组坐标变换
world coordinates -> camera coordinates
pixel coordinates -> image coordinates
目标是获得world coordinates -> image coordinates的变换, 缺少 camera coordinates -> pixel coordinates的变换, 这个变换需要利用小孔成像原理.

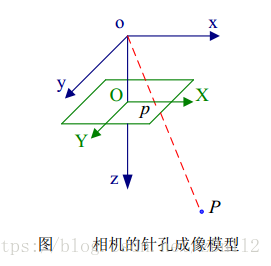
上图采用相机坐标系, o是光心,O是成像平面, $P(x_P,y_P,z_P)$ 是三维空间的一个物点, $p(x_p,y_p)$ 是P在像平面上的像点, $f = |oO|$ 是相机的焦距, 利用相似三角形对应边成比例可以得到
$x_p = \frac{x_P \times f}{z_P}$
$y_p = \frac{y_P \times f}{z_P}$
齐次坐标矩阵形式如下

$z P \times (x p, y p, 1) T = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ f, 0, 0, 0 0, f, 0, 0 0, 0, 1, 0 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ \times (x P, y P, z P, 1) T$ $z_P \times (x_p, y_p, 1)^T = \begin{bmatrix} f, 0, 0, 0 \\\\ 0, f,0,0 \\\\ 0, 0, 1, 0 \end{bmatrix} \times (x_P, y_P, z_P, 1)^T$
$z_P$ 可以当作一个比例因子 $s$ 处理
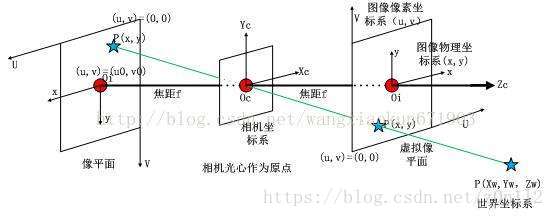
网上找了一个图,对几个坐标系有个直观的了解

相机内参/外参和透射变换

把上述几个坐标系变换合并在一起,得到

s \times [\begin{matrix} u \\ v \\ 1 \end{matrix}] = [\begin{matrix} \frac{1}{d X}, 0, u_{0} \\ 0, \frac{1}{d Y}, v_{0} \\ 0, 0, 1 \end{matrix}] [\begin{matrix} f, 0, 0, 0 \\ 0, f, 0, 0 \\ 0, 0, 1, 0 \end{matrix}] [\begin{matrix} R, T \\ 0, 1 \end{matrix}] [\begin{matrix} x_{w} \\ y_{w} \\ z_{w} \\ 1 \end{matrix}]

$s \times \begin{bmatrix} u \\\\ v \\\\ 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{dX}, 0, u_0 \\\\ 0, \frac{1}{dY}, v_0 \\\\ 0, 0, 1 \end{bmatrix} \begin{bmatrix} f, 0, 0, 0 \\\\ 0, f,0,0 \\\\ 0, 0, 1, 0 \end{bmatrix} \begin{bmatrix} R,T\\\\ 0,1 \end{bmatrix} \begin{bmatrix} x_w\\\\ y_w\\\\ z_w\\\\ 1 \end{bmatrix}$

= ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ a x, 0, u 0, 0 0, a y, v 0, 0 0, 0, 1, 0 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎡ ⎣ ⎢ R, T 0, 1 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ x w y w z w 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

$= \begin{bmatrix} a_x, 0, u_0, 0 \\\\ 0, a_y, v_0, 0 \\\\ 0,0,1,0 \end{bmatrix} \begin{bmatrix} R,T \\\\ 0,1 \end{bmatrix} \begin{bmatrix} x_w \\\\ y_w \\\\ z_w \\\\ 1 \end{bmatrix}$

= M 1 M 2 X w = M X w

$= M_1 M_2 X_w = M X_w$
其中

M1 M 1 ${M_1}$ 是相机的内参矩阵,

M2 M 2 ${M_2}$ 是相机的外参矩阵,

M M $M$ 是投影矩阵

M_{1} = [\begin{matrix} a_{x}, 0, u_{0}, 0 \\ 0, a_{y}, v_{0}, 0 \\ 0, 0, 1, 0 \end{matrix}]

$M_1 = \begin{bmatrix} a_x, 0, u_0, 0 \\\\ 0, a_y, v_0, 0 \\\\ 0,0,1,0 \end{bmatrix}$

M 2 = ⎡ ⎣ ⎢ R, T 0, 1 ⎤ ⎦ ⎥

$M_2 = \begin{bmatrix} R,T \\\\ 0,1 \end{bmatrix}$

畸变参数(distortion parameters)

畸变就是一条直线投影到图片上不能保持直线,原因很多,其中比较显著的两个是径向畸变和切向畸变.
这里写图片描述
实际位置和理想位置存在一定的角度差(切向畸变)和到中心的距离差(径向畸变)

径向畸变

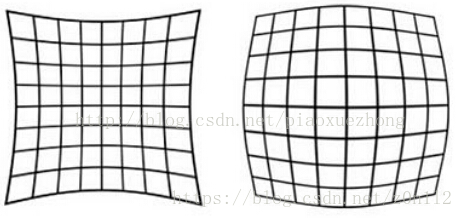
距离光心越远,径向位移越大,光心处没有畸变,左边时枕形畸变,右边时桶形畸变. 这种畸变可以用principle point(主点)周围的泰勒级数建模,公式如下

$x 0 = x (1 + k 1 r 2 + k 2 r 4 + k 3 r 6)$ $x_0 = x(1+k_1r^2+k_2r^4+k_3r^6)$
$y 0 = y (1 + k 1 r 2 + k 2 r 4 + k 3 r 6)$ $y_0 = y(1+k_1r^2+k_2r^4+k_3r^6)$
切向畸变

$x 0 = x + [2 p 1 y + p 2 (r 2 + 2 x 2)]$ $x_0 = x + [2p_1y + p_2(r^2+2x^2)]$
$y 0 = y + [2 p 2 x + p 1 (r 2 + 2 y 2)]$ $y_0 = y + [2p_2x + p_1(r^2+2y^2)]$

张友正标定法

摄像机标定就是计算出相机的内参,外参和畸变系数. 张友正标定法由于操作简单,精度高的优势而得到广泛应用. 其基本思路是:
* 通过拍摄标定板在不同角度下的图片
标定板上斑点的物理尺寸是要作为参数送入算法
* 提取特征点
* 计算单应性矩阵
* 计算内参
* 计算外参
* 计算畸变系数

提取特征点

提取特征点就是获得两幅图像中对应点的相对位置,每一个点对都可以提供两个方程,供后续求解操作

计算单应性矩阵

在计算视觉中,单应性是一个平面到另一个平面的投影映射 (PS: 这个单应性概念提出的很奇怪, 没有什么更深的含义的,名字和含义没看出什么关系).

s \times ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ u v 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ a x, 0, u 0, 0 0, a y, v 0, 0 0, 0, 1, 0 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎡ ⎣ ⎢ R, T 0, 1 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ x w y w z w 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ = M 1 M 2 X w = M X w

$s \times \begin{bmatrix} u \\\\ v \\\\ 1 \end{bmatrix} = \begin{bmatrix} a_x, 0, u_0, 0 \\\\ 0, a_y, v_0, 0 \\\\ 0,0,1,0 \end{bmatrix} \begin{bmatrix} R,T \\\\ 0,1 \end{bmatrix} \begin{bmatrix} x_w \\\\ y_w \\\\ z_w \\\\ 1 \end{bmatrix} = M_1 M_2 X_w = M X_w$
这里的M就是我们这一步的目标矩阵.上式是从世界坐标

(xw,yw,zw,1) ( x w , y w , z w , 1 ) $(x_w,y_w,z_w,1)$ 映射到图像坐标

s×(u,v,1) s × ( u , v , 1 ) $s \times (u,v,1)$ , 我们移动世界坐标系原点,可以令

zw=0 z w = 0 $z_w=0$ ,则有

s \times ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ u v 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ = M ¯ ¯ ¯ ¯ ¯ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ x w y w 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

$s \times \begin{bmatrix} u \\\\ v \\\\ 1 \end{bmatrix} = \overline{M} \begin{bmatrix} x_w \\\\ y_w \\\\ 1 \end{bmatrix}$

M¯¯¯¯¯ M ¯ $\overline{M}$ 是

3×3 3 × 3 $3 \times 3$ 的矩阵,而且因为齐次坐标的缘故,其最后一个元素是1,即只包含8个未知参数,需要至少4组点对(8个方程)即可求解单应性矩阵

M¯¯¯¯¯ M ¯ $\overline{M}$ (这里只是需要4组点对,一个标定板的图像就可以了)

计算内参

前面单应性矩阵 $\overline{M}$ 已经求解出来,我们把它写成三个列向量的形式

M ¯ ¯ ¯ ¯ ¯ = [m 1, m 2, m 3]

$\overline{M}=\begin{bmatrix} m_1,m_2,m_3 \end{bmatrix}$
同样我们把外参矩阵

M2 M 2 $M_2$ 也写成三个列向量的形式

M 2 = λ [r 1, r 2, t]

$M_2 = \lambda \begin{bmatrix} r_1, r_2,t\end{bmatrix}$
其中

r1 r 1 $r_1$ 是绕x轴旋转向量,

r2 r 2 $r_2$ 是绕y轴旋转向量,

t t $t$ 是平移向量,

λ

$\lambda$ 是一个比例因子,则有

[m 1, m 2, m 3] = λ M 1 [r 1, r 2, t]

$\begin{bmatrix} m_1, m_2, m_3 \end{bmatrix} = \lambda M_1 \begin{bmatrix} r_1, r_2,t \end{bmatrix}$

r 1 = M - 1 1 m 1

$r_1 = M_1 ^ {-1}m_1$

r 2 = M - 1 1 m 2

$r_2=M_1 ^ {-1}m_2$

r1 r 1 $r_1$ 和

r2 r 2 $r_2$ 满足如下两个限制
*

r1 r 1 $r_1$ 和

r2 r 2 $r_2$ 正交,即

rT1r2=0 r 1 T r 2 = 0 $r_1^Tr_2 = 0$
* 旋转向量的模是1,即

|r1|=|r2|=1 | r 1 | = | r 2 | = 1 $|r_1|=|r_2|=1$
消除

r1 r 1 $r_1$ 和

r2 r 2 ${r_2}$ 得到

m T 1 M - T 1 M - 1 1 m 2 = 0

$m_1^TM_1^{-T}M_1^{-1}m_2 = 0$

m T 1 M - T 1 M - 1 1 m 1 = m T 2 M - T 1 M - 1 1 m 2

$m_1^TM_1^{-T}M_1^{-1}m_1 = m_2^TM_1^{-T}M_1^{-1}m_2$
上面两个方程中

m1,m2 m 1 , m 2 $m_1, m_2$ 已经求解,则只有内参矩阵

M1 M 1 ${M_1}$ 待求解,

M1 M 1 $M_1$ 有4个未知量,则
至少需要两个单应性矩阵才可以求出内参矩阵

M1 M 1 $M_1$ (有的文献中

M1 M 1 $M_1$ 有5个未知量,则至少需要三个单应性矩阵). 一个角度下的棋盘图只能获得一个单应性矩阵,所以至少需要两幅不同角度下的棋盘图才可以求解出内参矩阵

计算外参

我们再回到下面这个式子

[m 1, m 2, m 3] = λ M 1 [r 1, r 2, t]

$\begin{bmatrix} m_1, m_2, m_3 \end{bmatrix} = \lambda M_1 \begin{bmatrix} r_1, r_2,t \end{bmatrix}$
现在单应性矩阵

[m 1, m 2, m 3]

$\begin{bmatrix} m_1, m_2, m_3 \end{bmatrix}$
和内参

M1 M 1 $M_1$ 已知

r1=λM−1m1 r 1 = λ M − 1 m 1 $r_1 = \lambda M^{-1}m_1$

r2=λM−1m2 r 2 = λ M − 1 m 2 $r_2 = \lambda M^{-1}m_2$

r3=r1×r2 r 3 = r 1 × r 2 $r_3 = r_1 \times r_2$

t=λM−1m3 t = λ M − 1 m 3 $t = \lambda M^{-1} m_3$
其中

λ λ $\lambda$ 是比例因子,需要保证

|r1|=|r2|=1 | r 1 | = | r 2 | = 1 $|r_1|=|r_2|=1$ ,所以

λ = 1 M - 1 1 m 1 = 1 M - 1 1 m 2

$\lambda = \frac{1}{M_1^{-1}m_1} = \frac{1}{M_1^{-1}m_2}$

* $r_3$ 是怎么出来的 ?????????? *

计算畸变系数

上面给出求解参数需要的最小点对数和最小标定图数目只时理想情况下的理论值,实际中考虑到噪声的存在,需要用多组数据,利用最优化方法求解相机参数, 张氏标定法中采用Levenberg-Marquardt求解最大似然估计,获得参数和畸变参数

参考资料

http://blog.youkuaiyun.com/lql0716
https://blog.youkuaiyun.com/zkl99999/article/details/48372203
https://blog.youkuaiyun.com/piaoxuezhong/article/details/75268535