你好!我是Johngo!
动态规划作为面试的重镇之地,都有。。
不同路径 爬楼梯!
打家劫舍 卖股票!
单词拆分 接雨水!
其实是这样,突然想到今年夏天,大学同宿舍在抖音的总监中,让他用动态规划的思路解决「最长公共子序列」的一道题目。
不过作为一个游戏通关者而言,确实不太难!因为他心目中的总监面应该是很难的!
但是,万万没有想到,这仅仅是开始…总监面今天就到这里了,下期分享他后面遇到了什么??!!

好了,先把总监面开始遇到的问题跟大家分享,正好对应 LeetCode专题「字符串」的第 5 期。
趁着对那次面试还有点印象,赶紧记录下来!
本来想要把「最长公共子序列」和「最长上升子序列」一起和大家把思路分享一下,都属于可以使用动态规划的思想进行解决。但貌似还是两块内容。
所以,今天先把「最长公共子序列」分享出来和大家聊聊。
后面再出一期把「最长上升子序列」详细的分享,后面这一期内容估计会比较多。
题外话,上一期的抽书活动还没有结束,感兴趣的可以继续参与哈!【 https://mp.weixin.qq.com/s/V9srFVVrDxVRW8XYNK8pLg 】
说在前面
言归正传,这一期来说说字符串的第五块内容 「字符串 - 最长公共子序列」
github:https://leetcode-cn.com/problems/longest-common-subsequence/
文档地址:https://github.com/xiaozhutec/share_leetcode/tree/master/docs
整体架构(github中可查看高清图):

字符串 - 最长公共子序列
今天这期内容是字符串的第 5 期。
之前谈到过子串和子序列的区别,子串指的是向字符串截取固定长度的子字符串。
而子序列在LeetCode有过解释:
一个字符串的子序列是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
既然是公共子序列,涉及到的肯定至少是两个字符串的公共子序列比较
比如:
text1 = "abcde", text2 = "ace"
它的公共元素就是"ace"。
如何在两个字符串中找到其公共的公共的部分,首先想到的肯定是暴力求解,逐项对比。最先想到,然而也是最先放弃的,因为时间复杂度最高。这块也不做讨论。
其次,最先想到的是动态规划来解决,记录遍历时的每一个状态。
关于动态规划的部分,之前已经完整的写过一篇,超过万字,非常全面【 https://mp.weixin.qq.com/s/ZqOWomyra90BRzNukHr3-Q 】
案例
整体关于字符串「最长公共子序列」方面的问题一般来说都会用动态规划的思想去解决!
下面会通过一个典型案例具体来看是怎么解决的,使用 LeetCode 的 1143 题 进行举例。
1143.最长公共子序列【中等】
1143.最长公共子序列【中等】
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列的长度。如果不存在公共子序列 ,返回 0 。
一个字符串的子序列是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace" ,它的长度为 3 。
这里用动态规划的思想进行解决。对于两个字符串的比较,一定会涉及到利用二维数组来进行解决。
按照之前说的四步骤,动态数组定义、初始化、状态转移方程、优化、、。
以下利用字符串 “abcde" 和 ”ace” 为例,计算最长公共子序列。
令 s1=“abcde”, s2=“ace”
一、动态数组定义
根据s1的长度为5,s2的长度为3。
初始化一个 3 行 5 列的二维数组dp,赋初值全为 0。用来存储动态规划过程中记录的值。
d p [ i ] [ j ] dp[i][j] dp[i][j] 代表位置 ( i , j ) (i, j) (i,j) 最长公共子序列的值!

二、初始化
针对动态规划一般的初始化方法,一定是边界的初始化。
这里是二维数组,咱们这里要初始化的地方是第 0 行和第 0 列。
① 针对 0 行
s1=“abcde”, s2=“ace”,s2[0] 与 s1 的每一个字符进行比较,只有第 0 位置字符是相同的,第 0 位置为 1。由于公共子序列的规则,那第 0 行初始化全为 1。

① 针对 0 列
s1=“abcde”, s2=“ace”,s1[0] 与 s2 的每一个字符进行比较,同样只有第 0 位置字符是相同的,第 0 位置为 1。依然是由于公共子序列的规则那第 0 列初始化全为 1。

根据初始化的情况,下面用代码描述:
if text1[0] == text2[0]:
dp[0][0] = 1
for i in range(1, size1):
dp[0][i] = 1 if dp[0][i-1] == 1 else int(text1[i] == text2[0])
for j in range(1, size2):
dp[j][0] = 1 if dp[j-1][0] == 1 else int(text2[j] == text1[0])
三、状态转移方程
很明显可以分为两种情况:
- 当前位置的字符相同
- 当前位置的字符不相同
① 当 text1[i] == text2[j] 的时候,说明当前字符相同,只要将上一个字符对应的 dp 的值加 1 就可以了。即 dp[i][j] = dp[i-1][j-1] + 1。
注意,这里一定是 dp[i-1][j-1],因为此处的字符相同。那么,要想计算此处 dp[i][j] 的值,一定是与位置 i-1 与 j-1 的位置相关的。
② 当 text1[i] != text2[j] 的时候,此时当前字符不相同,那么此处 dp[i][j] 的数值一定沿用上一个 dp 的数值。所以,取得一定是其中的最大值 max(dp[i-1][j], dp[i][j-1])。
综上所述,可以得到该问题的状态转移方程:
$$
dp[i][j]= \begin{cases}
dp[i-1][j-1] + 1, & text1[i] = text2[j] \[2ex]
max(dp[i-1][j], dp[i][j-1]), & text1[i] \neq text2[j]
\end{cases}
$$
从位置 (1, 1) 位置开始计算,判断两个字符串在当前字符串是否相等:
-
如果相等,则取dp[i-1][j-1]+1
-
如果不相等,则取max(dp[i][j-1], dp[i-1][j])
根据上述的状态转移方程,以及s1=“abcde”, s2=“ace”,下面把二维数组填满,得到最后的答案!
① 位置(1,1): s 1 [ 1 ] ≠ s 2 [ 1 ] = > d p [ 1 ] [ 1 ] = m a x ( d p [ 0 ] [ 1 ] , d p [ 1 ] [ 0 ] ) = 1 s1[1] \neq s2[1] => dp[1][1]=max(dp[0][1], dp[1][0])=1 s1[1]=s2[1]=>dp[1][1]=max(dp[0][1],dp[1][0])=1

② 位置(1,2): s 1 [ 2 ] = = s 2 [ 1 ] = > d p [ 1 ] [ 2 ] = d p [ 0 ] [ 0 ] + 1 s1[2] == s2[1] => dp[1][2]=dp[0][0]+1 s1[2]==s2[1]=>dp[1][2]=dp[0][0]+1
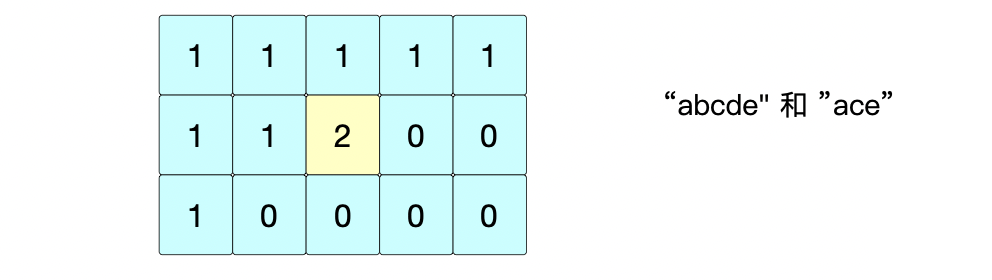
③ 位置(1,3): s 1 [ 3 ] ≠ s 2 [ 1 ] = > d p [ 1 ] [ 3 ] = m a x ( d p [ 0 ] [ 3 ] , d p [ 1 ] [ 2 ] ) = 2 s1[3] \neq s2[1] => dp[1][3]=max(dp[0][3], dp[1][2])=2 s1[3]=s2[1]=>dp[1][3]=max(dp[0][3],dp[1][2])=2

④ 位置(1,4): s 1 [ 4 ] ≠ s 2 [ 1 ] = > d p [ 1 ] [ 4 ] = m a x ( d p [ 0 ] [ 4 ] , d p [ 1 ] [ 3 ] ) = 2 s1[4] \neq s2[1] => dp[1][4]=max(dp[0][4], dp[1][3])=2 s1[4]=s2[1]=>dp[1][4]=max(dp[0][4],dp[1][3])=2

⑤ 位置(2,1): s 1 [ 1 ] ≠ s 2 [ 2 ] = > d p [ 2 ] [ 1 ] = m a x ( d p [ 2 ] [ 0 ] , d p [ 1 ] [ 1 ] ) = 1 s1[1] \neq s2[2] => dp[2][1]=max(dp[2][0], dp[1][1])=1 s1[1]=s2[2]=>dp[2][1]=max(dp[2][0],dp[1][1])=1

⑥ 位置(2,2): s 1 [ 2 ] ! = s 2 [ 2 ] = > d p [ 2 ] [ 2 ] = m a x ( d p [ 2 ] [ 1 ] , d p [ 1 ] [ 2 ] ) = 2 s1[2] != s2[2] => dp[2][2]=max(dp[2][1], dp[1][2])=2 s1[2]!=s2[2]=>dp[2][2]=max(dp[2][1],dp[1][2])=2
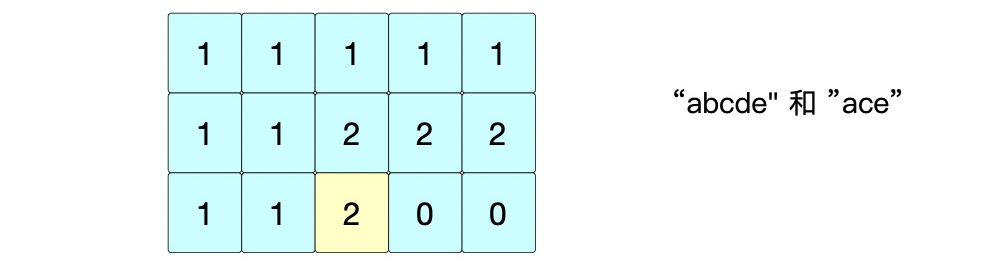
⑦ 位置(2,3): s 1 [ 3 ] ! = s 2 [ 2 ] = > d p [ 2 ] [ 3 ] = m a x ( d p [ 2 ] [ 2 ] , d p [ 1 ] [ 3 ] ) = 2 s1[3] != s2[2] => dp[2][3]=max(dp[2][2], dp[1][3])=2 s1[3]!=s2[2]=>dp[2][3]=max(dp[2][2],dp[1][3])=2

⑧ 位置(2,4): s 1 [ 4 ] = = s 2 [ 2 ] = > d p [ 2 ] [ 4 ] = d p [ 1 ] [ 3 ] + 1 = 3 s1[4] == s2[2] => dp[2][4]=dp[1][3]+1=3 s1[4]==s2[2]=>dp[2][4]=dp[1][3]+1=3

这个就是二维数据中,每一格的填充方式。
根据上述的一个清晰的思路,状态转移填充二位数组的代码描述:
for i in range(1, size2):
for j in range(1, size1):
if text2[i] == text1[j]:
# 注意这里是dp[i-1][j-1]+1
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i][j-1], dp[i-1][j])
return dp[-1][-1]
好了,这个是一个全面的答案:
def longestCommonSubsequence(self, text1, text2):
size1 = len(text1)
size2 = len(text2)
# 1 先定义 dp 数组
dp = [[0 for _ in range(size1)] for _ in range(size2)]
# 2 初始化 dp 数组的第 0 行和第 0 列
if text1[0] == text2[0]:
dp[0][0] = 1
for i in range(1, size1):
dp[0][i] = 1 if dp[0][i-1] == 1 else int(text1[i] == text2[0])
for j in range(1, size2):
dp[j][0] = 1 if dp[j-1][0] == 1 else int(text2[j] == text1[0])
# 3 动态方程进行求解
for i in range(1, size2):
for j in range(1, size1):
if text2[i] == text1[j]:
# 注意这里是dp[i-1][j-1]+1
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i][j-1], dp[i-1][j])
return dp[-1][-1]
最后, d p [ − 1 ] [ − 1 ] dp[-1][-1] dp[−1][−1] 代表的就是最后一个位置的值,也是截止到最后最长公共子序列的最大值!
以上就是该类型题目使用动态规划的常规思路了。
为什么说常规思路?因为一般情况下动态规划问题可以有空间方面的优化,而且该类型题目上述解决方案中是有优化空间的。
四、优化
在很多时候,咱们遇到使用动态规划利用二维数据解决问题的时候,通常可以进行空间方面的优化。
在之前的文章有很详细的说明,有兴趣大家可以看看【 https://mp.weixin.qq.com/s/ZqOWomyra90BRzNukHr3-Q 】
因为通常,在二维的情况下,当前 ( i , j ) (i, j) (i,j)的取值,最多只与上一个位置或者左面位置的值有关系,而与跨行或者跨列是没有关系的。
比如说在计算位置(2,3)的时候: s 1 [ 3 ] ! = s 2 [ 2 ] = > d p [ 2 ] [ 3 ] = m a x ( d p [ 2 ] [ 2 ] , d p [ 1 ] [ 3 ] ) = 2 s1[3] != s2[2] => dp[2][3]=max(dp[2][2], dp[1][3])=2 s1[3]!=s2[2]=>dp[2][3]=max(dp[2][2],dp[1][3])=2

发现是与第 0 行以及之前和第 1 列以及之前的所有数据都是没有关系的,所以可以从这方面进行空间的优化。
空间上除了定义变量外,一个2行2列的二维数组就可以解决!
有兴趣的同学可以在评论区写出优化后的代码,或者如果有需要,在评论区留言,我在后面文章中进行这类题目关于优化方式的分享!
好了,今天就关于字符串「最长公共子序列」进行了分享。
另外,方便的话也在我的github👇 加颗星,它是我持续输出最大最大的动力,感谢大家!
github:https://github.com/xiaozhutec/share_leetcode
对了,「一周送书」上周的抽书活动还没有结束,感兴趣的可以继续参与哈!
如果感觉内容对你有些许的帮助,求点赞,求在看!
下期想看哪方面的,评论区告诉我!
咱们下期见!bye~~








 本文详细介绍了如何使用动态规划解决字符串的最长公共子序列问题,以LeetCode 1143题为例,阐述了动态规划的定义、初始化、状态转移方程和优化过程,提供了一种寻找两个字符串共同子序列的高效方法。
本文详细介绍了如何使用动态规划解决字符串的最长公共子序列问题,以LeetCode 1143题为例,阐述了动态规划的定义、初始化、状态转移方程和优化过程,提供了一种寻找两个字符串共同子序列的高效方法。
















 1489
1489

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








