PLA
由于PLA针对线性可分数据集,因此在此选择Pocket PLA算法进行实现,文章记录针对cifar100数据集的实现,由于PLA算法过于简单,因此准确率很低,但仅作为一次尝试。
一、加载数据
1.导入数据
from keras.datasets import cifar100
(x_train, y_train), (x_test, y_test) = cifar100.load_data(label_mode='fine')
官网介绍:CIFAR100 小图像分类数据集
50,000 张 32x32 彩色训练图像数据,以及 10,000 张测试图像数据,总共分为 100 个类别。
加载过慢
由于数据集较大,加载时速度较慢,可以等待其下载,或者直接点击链接进行下载,将下载好的数据集放在keras数据集的指定位置,即可直接加载数据集。

注意路径,直接将cifar-100-python.tar.gz文件放进去即可。(下不下来数据集的可以找我~)

加载成功~
2.探索数据

3.处理数据
(1)由于数据集过大,我们选取其中的500个样本进行操作,并按照3:1的比例划分数据集。

(2)将数据打平,方便后续处理

至此,数据处理基本结束。后续会根据算法进行X和Y的具体调整。整理成函数如下。
参数num:加载数据的个数,例如本次实验以500个数据集为例,调用时load_cifar100(500)即可,想换数据集大小改变参数即可
def load_cifar100(num):
# 加载数据集
(x_train, y_train), (x_test, y_test) = cifar100.load_data(label_mode='fine')
x = x_train[:num]
y = y_train[:num]
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=0)
X_train = X_train.reshape((X_train.shape[0], -1)).T
X_test = X_test.reshape((X_test.shape[0], -1)).T
y_train = y_train.reshape((y_train.shape[0], -1)).T
y_test = y_test.reshape((y_test.shape[0], -1)).T
return X_train,X_test,y_train,y_test
二、PLA算法
1.编写代码

根据算法,进行编写代码。
算法:(pocket PLA)----数据不是线性可分
1.随机初始化参数,计算在初始化的直线中分类错误的个数。
2.随机挑选一个误分类点,进行修正,计算分类错误点数,并与之前错误个数进行比较,取个数较小的直线为当前选择的分类直线
3.经过n次迭代后,选择个数最小的直线对应的w,为我们最终得到的想要的权重值
def model_PLA(X_train, y_train, X_test, y_test, iteration):
'''
构建一个PLA模型
:param X_train: feature (nx+1,m)
:param y_train: label (1,m)
:param iteration:迭代轮数
:param w:参数 (nx+1,1)
:return:
'''
#初始化参数
w = init_para(X_train)
# 存放E_in和E_out
E_in = []
E_out = []
# 初始值的结果
y_pred = np.sign(np.dot(w.T, X_train)) # 预测
error = y_pred != y_train # 找到错误点
error_num_now = np.sum(error) # 计算错误点个数
y_pred_test = np.sign(np.dot(w.T, X_test)) # 预测
error_test = y_pred_test != y_test # 找到错误点
error_num_test = np.sum(error_test) # 计算错误点个数
E_in.append(error_num_now)
E_out.append(error_num_test)
# 设置迭代次数
for i in range(iteration):
# 随机选择一个错误点
error_idex = np.where(error == True)[1] # 返回错误点所在的索引值为一个一维的数组(np.array([]),),取[1]
idex_1 = np.random.randint(error_num_now) # 随机选择一个值的索引值
idex = error_idex[idex_1]
x_i = X_train[:, idex].reshape(X_train.shape[0], 1)
y_i = y_train[0, idex].reshape(y_train.shape[0], 1)
w_new = w + np.multiply(y_i, x_i) # 修正
# 判断是否更新
y_pred_new = np.sign(np.dot(w_new.T, X_train)) # 预测
error_new = y_pred_new != y_train # 找到错误点
error_num_new = np.sum(error_new) # 计算错误点个数
#print("更新前的错误点数为{}".format(error_num_now))
#print("修正后{}".format(error_num_new))
if error_num_new.item() < error_num_now.item():
# 更新后错误率变小,更新;否则不更新
w = w_new
error = error_new
error_num_now = error_num_new
y_pred_test = np.sign(np.dot(w.T, X_test)) # 预测
error_test = y_pred_test != y_test # 找到错误点
error_num_test = np.sum(error_test) # 计算错误点个数
E_in.append(error_num_now)
E_out.append(error_num_test)
if error_num_new.item() == 0:
break
return w, E_in, E_out, i
2.附带代码:
1.随机初始化:
def init_para(train_x):
#初始化参数,随机生成高斯分布
nx = train_x.shape[0]
w = np.random.randn(nx,1)
return w
三、主函数
1.Y处理:由于PLA为二分类算法,因此将Y标签(100类)变为两类,小于50为一类,标为1,其余算为一类,标为-1.
def convert_y(y):
y_index_large = y >= 50
y[y_index_large] = -1
y_index_small = y_index_large==False
y[y_index_small] = 1
return y
2.X处理:这门课中讲的算法,实际上将偏置直接算成了W0,合并在了W中,因此X也需要合并X0,即特征拼接一维全为1的向量。(由于编写PLA算法时按照这个思路写的,所以需要修改X,否则不修改的话直接用w,b也行)
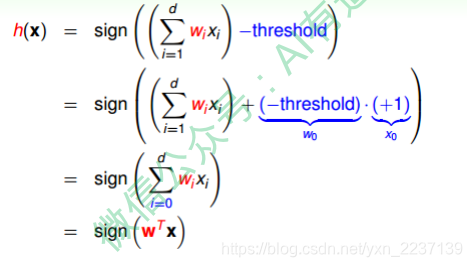
def convert_x(x):
#拼接x0
x0 = np.ones((1,x.shape[1]))
x_convert = np.concatenate((x,x0),axis=0)
return x_convert
3.计算Error
拿在模型训练过程中统计的值进行归一化,并返回最终结果。
def error(X,E):
num = X.shape[1]
E = [round(x / num, 3) for x in E]
Error = E[-1]
return E,Error
计算Ein和Eout的方法:
y_pred_test = np.sign(np.dot(w.T, X_test)) # 预测
error_test = y_pred_test != y_test # 找到错误点
error_num_test = np.sum(error_test) # 计算错误点个数
懒得封装函数了,直接在PLA的模型中。其实就是比较预测结果和真值,最终得到预测错的点数。在error()函数中除以总数进行归一化,用的是0/1error。

PS:其实感觉直接np.mean(error_test)就可以了,不需要求和再归一化,好多numpy的函数还不知道,还得继续学习。
4.画图(E_in和E_out)
将E_in和E_out画在一个图上
def draw(E_in,E_out,iteration):
# 画出E_in和E_out
x = range(iteration + 1)
# 设置图形大小
plt.figure(figsize=(20, 8), dpi=80)
# color可以百度颜色代码
plt.plot(x, E_in, label="E_in", color="r")
plt.plot(x, E_out, label="E_out", color="b")
# 设置x轴刻度
xtick_labels = ["{}".format(i) for i in x]
plt.xticks(x, xtick_labels)
# 添加图例
plt.legend(loc="upper right")
# 展示
plt.show()
5.整合
def main():
# 加载数据集
X_train, X_test, y_train, y_test = load_cifar100(500)
# 修正数据集
X_train = convert_x(X_train)
X_test = convert_x(X_test)
y_train = convert_y(y_train)
y_test = convert_y(y_test)
iteration = 30
w, ein, eout, i= model_PLA(X_train, y_train, X_test, y_test, iteration)
E_in,E_in_final = error(X_train,ein)
E_out, E_out_final = error(X_test, eout)
print("Ein:{}".format(E_in_final))
print("Eout:{}".format(E_out_final))
draw(E_in,E_out,i+1)
至此,Pocket PLA(cifar100)的代码已经全部编写好啦!
四、总结
代码整合起来如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from keras.datasets import cifar100
def init_para(train_x):
#初始化参数,随机生成高斯分布
nx = train_x.shape[0]
w = np.random.randn(nx,1)
return w
def convert_x(x):
#拼接x0
x0 = np.ones((1,x.shape[1]))
x_convert = np.concatenate((x,x0),axis=0)
return x_convert
def convert_y(y):
y_index_large = y >= 50
y[y_index_large] = -1
y_index_small = y_index_large==False
y[y_index_small] = 1
return y
def load_cifar100(num):
# 加载数据集
(x_train, y_train), (x_test, y_test) = cifar100.load_data(label_mode='fine')
x = x_train[:num]
y = y_train[:num]
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=0)
X_train = X_train.reshape((X_train.shape[0], -1)).T
X_test = X_test.reshape((X_test.shape[0], -1)).T
y_train = y_train.reshape((y_train.shape[0], -1)).T
y_test = y_test.reshape((y_test.shape[0], -1)).T
return X_train,X_test,y_train,y_test
def model_PLA(X_train, y_train, X_test, y_test, iteration):
'''
构建一个PLA模型
:param X_train: feature (nx+1,m)
:param y_train: label (1,m)
:param iteration:迭代轮数
:param w:参数 (nx+1,1)
:return:
'''
#初始化参数
w = init_para(X_train)
# 存放E_in和E_out
E_in = []
E_out = []
# 初始值的结果
y_pred = np.sign(np.dot(w.T, X_train)) # 预测
error = y_pred != y_train # 找到错误点
error_num_now = np.sum(error) # 计算错误点个数
y_pred_test = np.sign(np.dot(w.T, X_test)) # 预测
error_test = y_pred_test != y_test # 找到错误点
error_num_test = np.sum(error_test) # 计算错误点个数
E_in.append(error_num_now)
E_out.append(error_num_test)
# 设置迭代次数
for i in range(iteration):
# 随机选择一个错误点
error_idex = np.where(error == True)[1] # 返回错误点所在的索引值为一个一维的数组(np.array([]),),取[1]
idex_1 = np.random.randint(error_num_now) # 随机选择一个值的索引值
idex = error_idex[idex_1]
x_i = X_train[:, idex].reshape(X_train.shape[0], 1)
y_i = y_train[0, idex].reshape(y_train.shape[0], 1)
w_new = w + np.multiply(y_i, x_i) # 修正
# 判断是否更新
y_pred_new = np.sign(np.dot(w_new.T, X_train)) # 预测
error_new = y_pred_new != y_train # 找到错误点
error_num_new = np.sum(error_new) # 计算错误点个数
if error_num_new.item() < error_num_now.item():
# 更新后错误率变小,更新;否则不更新
w = w_new
error = error_new
error_num_now = error_num_new
y_pred_test = np.sign(np.dot(w.T, X_test)) # 预测
error_test = y_pred_test != y_test # 找到错误点
error_num_test = np.sum(error_test) # 计算错误点个数
E_in.append(error_num_now)
E_out.append(error_num_test)
if error_num_new.item() == 0:
break
return w, E_in, E_out, i
def error(X,E):
num = X.shape[1]
E = [round(x / num, 3) for x in E]
Error = E[-1]
return E,Error
def draw(E_in,E_out,iteration):
# 画出E_in和E_out
x = range(iteration + 1)
# 设置图形大小
plt.figure(figsize=(20, 8), dpi=80)
# color可以百度颜色代码
plt.plot(x, E_in, label="E_in", color="r")
plt.plot(x, E_out, label="E_out", color="b")
# 设置x轴刻度
xtick_labels = ["{}".format(i) for i in x]
plt.xticks(x, xtick_labels)
# 添加图例
plt.legend(loc="upper right")
# 展示
plt.show()
def main():
# 加载数据集
X_train, X_test, y_train, y_test = load_cifar100(500)
# 修正数据集
X_train = convert_x(X_train)
X_test = convert_x(X_test)
y_train = convert_y(y_train)
y_test = convert_y(y_test)
iteration = 30
w, ein, eout ,i= model_PLA(X_train, y_train, X_test, y_test, iteration)
E_in,E_in_final = error(X_train,ein)
E_out, E_out_final = error(X_test, eout)
print("Ein:{}".format(E_in_final))
print("Eout:{}".format(E_out_final))
draw(E_in,E_out,i+1)
if __name__ == "__main__":
main()
测试
怎么也想不到,这个数据集居然线性可分了。。。重新找了2个小时的bug,然后加了全部分类正确就break的代码。。。代码已经更新了,如果全部分类正确就可以直接结束。现在在线性可分和不可分的数据集上应该都能用了。

打印了一下最终训练好的w看了一下,好像也没什么问题。100类的图像分成两类居然线性可分。。。不知道是不是错了

总结
虽然在这个数据集上有点诡异,但是这个算法在自动生成的线性不可分的数据集make_moons()和mnist数据集上都可以正常运行,都验证过。结果大致是下图的形式。

























 246
246

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








