先序中序,后序中序,中序层序都可以唯一确定一棵树;
先序后序无法还原树的原因:当只有一棵子树时无法确定是左子树还是右子树;
写了一下中序层序还原树的递归和非递归方法。
用于检验算法的二叉树
中序序列为:6 7 4 11 2 5 9 8 10 1 3
层序序列为:2 7 5 6 11 1 4 8 3 9 10
递归方法
对于元素唯一的序列,记录层序各结点对应的下标,中序遍历序列的根节点肯定是在层序序列中下标数最小的结点!
- 代码
#include<bits/stdc++.h>
using namespace std;
#define N 1000
typedef struct node
{
int v;
node *l,*r;
}*pnode;
int car[N],inar[N];
map<int,int> cvis;
pnode func(int l,int r)
{
pnode p=NULL;
if(l<r)
{
p=(pnode)malloc(sizeof(node));
int mid=l;
for(int i=l+1;i<r;i++)
if(cvis[inar[mid]]>cvis[inar[i]])
mid=i;
p->v=inar[mid];
p->l=func(l,mid);
p->r=func(mid+1,r);
}
return p;
}
void preorder(pnode p) //先序遍历
{
if(p)
{
printf("%d ",p->v);
preorder(p->l);
preorder(p->r);
}
}
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
for(int i=0;i<n;i++)
scanf("%d",&inar[i]);
for(int i=0;i<n;i++)
{
scanf("%d",&car[i]);
cvis[car[i]]=i;
}
pnode BTree;
BTree=func(0,n);
preorder(BTree);
printf("\n");
}
return 0;
}
-
运行结果

非递归方法
因为层序是使用队列来进行遍历的,所以还原时也可以用队列进行,层序序列确定根结点,中序序列确定左右子树,随后在队列中记录每个子树对应的根结点,根节点的前序为-1,如果存在结点才需要对层序对应值i++!
可以用孩子表示法,或者双亲表示法来保存结果,只要对孩子表示的结果递归处理就可以得到二叉链表的存储结果。
- 代码
#include<bits/stdc++.h>
using namespace std;
#define N 100
typedef int DataType;
struct cnode //双亲建树
{
int p;
int l,r;
cnode(){
}
cnode(int p,int l,int r):p(p),l(l),r(r){
}
};
int parents[N];
vector<int> child[N];
DataType ar1[N],ar2[N];
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
for(int i=0;i<n;i++) //中序
scanf("%d",&ar1[i]);
for(int i=0;i<n;i++) //层序
scanf("%d",&ar2[i]);
memset(parents,-1,sizeof(parents));
queue<cnode> que;
que.push(cnode(-1,0,n));
int i=0;
while(!que.empty())
{
cnode m=que.front();
que.pop();
if(m.l<m.r)
{
int v=ar2[i];
int k=m.l;
while(ar1[k]!=v&&k<m.r)
k++;
parents[k]=m.p;
if(m.p!=-1)
child[m.p].push_back(k);
que.push(cnode(k,m.l,k));
que.push(cnode(k,k+1,m.r));
i++; //!!!
}
}
printf("\n孩子表示法\n");
for(int i=0;i<n;i++)
{
if(child[i].size()==0)
printf("%d is leaf\n",ar1[i]);
else
{
printf("%d kids:",ar1[i]);
for(int j=0;j<child[i].size();j++)
printf(" %d",ar1[child[i][j]]);
puts("");
}
}
printf("\n双亲表示法\n");
for(int i=0;i<n;i++)
printf("%d p:%d\n",ar1[i],parents[i]==-1?-1:ar1[parents[i]]);
}
return 0;
}
-
运行结果
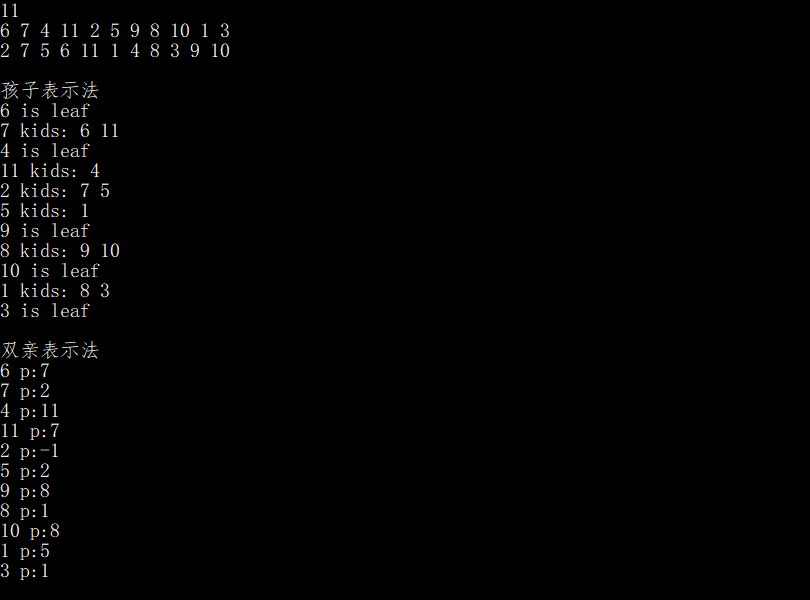







 本文介绍了如何通过中序和层序序列还原二叉树,重点讲解了递归和非递归两种方法。递归方法利用中序序列中根节点的下标最小的特点;非递归方法则借助队列,结合层序和中序序列确定子树。文中提供了具体的代码实现和运行结果。
本文介绍了如何通过中序和层序序列还原二叉树,重点讲解了递归和非递归两种方法。递归方法利用中序序列中根节点的下标最小的特点;非递归方法则借助队列,结合层序和中序序列确定子树。文中提供了具体的代码实现和运行结果。

















 1456
1456

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








