C语言 关于位运算的一些算法和算法题

前言

我们在前面讲运算符的时候, 说到了一个位运算符, 这一部分呢? 我们就来聊聊一些常见的关于位运算的一些算法和与其相关得到算法题叭~~

常见的位运算算法总结

1 基础的位运算小结

<<    左移    >>   优异     ~    按位取反    
&    有0为0    |    有1为1    ^   相同为0, 相异为1, 无进位相加

这里简单说一下这个 无进位相加 是什么?

给定两个二进制序列, 让两个 bit位 相加, 不管进位部分, 就是异或的运算规律, 比如:

0110 1010

0111 0010

--------------

0001 1000

2 给一个数n, 确定他的二进制序列中第x位是0还是1 ?

我们这里先规定好, 第几位, 我们是从右边的低位为第0位, 向左位数增加

比如一个二进制序列: 0010 1110 1010 1001

最右边的1 为第0位~~

我们的做法是, 让这个二进制序列, 向右移x位,  之后&1, 看结果, 如果是1则为1, 如果为0则为0, 如下

(n >> x) & 1

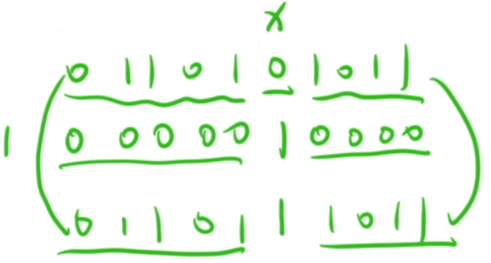
3 将一个数n的二进制序列的第x位修改成1

我们的想法是让其他位不变, 让第x位成1, 那么想一下只要让原来的数或上0, 是不变的, 但是让想要改变的哪一位 | 上一个1, 如果原来是 1, 那么结果是1, 如果原来为0, 那么结果也为1, 所以我们就可以:

我们让原来的 n |= (1 << x) 就可以了~, 原理如下: 

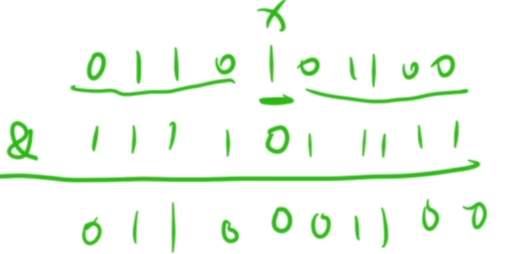
4 将一个数n的二进制序列的第x位修改成0

n &= (~(1 << x))        

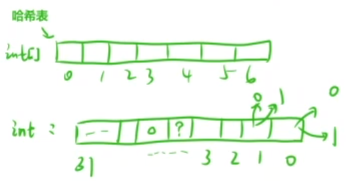
5 位图思想

先简单说一下什么是位图, 位图就是一个哈希表, 哈希表我们使用一个整数数组来的值来记录一些信息, 但是现在如果我们只需要表示有无, 我们就可以使用每一个位, 如果有这一位为1, 如果没有这一位位0

前面说到的三种操作, 在位图中会大量的使用~~ 

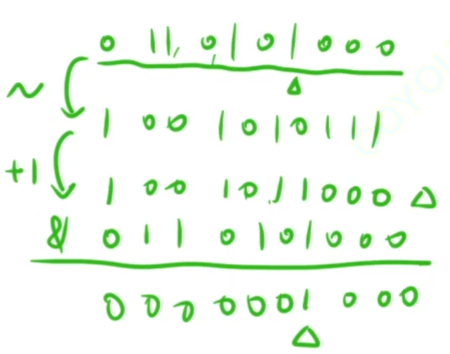
6 提取一个数n, 二进制表示中最右侧的1

这个操作, 我们有一个名字叫做 lowbit

一个数 转化为他的相反数, 在二进制序列上是 按位取反 再+1, 这个在原码补码反码的地方学习到的

所以 n转化为 -n 的本质是: 将最右侧1的右侧保持不变, 左侧严格按位取反

n & (-n)

7 干掉一个数n, 二进制表示中最右侧的1

n & (n - 1)

让二进制序列去借位, 如果没有1就一直借位, 直到遇上1 , 这样让借位的地方, 左边全部不变, 右边全部相反

8 位运算的优先级

优先级这里我其实不是想说优先级, 而是想说 我们能加括号就加括号, 让加括号的先算就行了~~, 避免去记忆太多的东西~

9 异或运算的运算律

1. a ^ 0 = a    任何一个数与0异或是他本身

2. a ^ a = 0    相同的两个数异或为0

3. a ^ b ^ c = a ^ (b ^ c)  交换律不考虑顺序

常见的位运算算法题

使用上面的 7和8, 就可以解决LeetCode中的: 191, 338, 461题

191. 位1的个数

338. 比特位计数

461. 汉明距离

使用上面的 9, 可以解决 LeetCode中的: 136. 只出现一次的数1 和 260. 只出现一次的数3

136. 只出现一次的数字

260. 只出现一次的数字 III

面试题 01.01. 判定字符是否唯一

268. 丢失的数字

371. 两整数之和

137. 只出现一次的数字 II

面试题 17.19. 消失的两个数字