力扣 python 简单题第二轮1

最新推荐文章于 2025-12-12 23:14:46 发布

原创最新推荐文章于 2025-12-12 23:14:46 发布 · 441 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #职场和发展

101. 对称二叉树

递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        # 1 递归
        def recursive(l:Optional[TreeNode],r:Optional[TreeNode]):
            if l is None or r is None:
                return l==r
            return l.val==r.val and recursive(l.left,r.right) and recursive(l.right,r.left)
        return recursive(root.left,root.right)

迭代

递归变迭代的常用方法，引入队列。

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        return self.check(root, root)
    
    def check(self, u: TreeNode, v: TreeNode) -> bool:
        q = deque()
        q.append(u)
        q.append(v)
        
        while q:
            u = q.popleft()
            v = q.popleft()
            
            if not u and not v:
                continue
            if not u or not v:
                return False
            if u.val != v.val:
                return False
            
            # 将 u 的左子树与 v 的右子树配对入队
            q.append(u.left)
            q.append(v.right)
            
            # 将 u 的右子树与 v 的左子树配对入队
            q.append(u.right)
            q.append(v.left)
        
        return True

110. 平衡二叉树

方法一：自顶向下的递归

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        # 先写递归
        def recursive(root:Optional[TreeNode])->int:
            if not root: return 0
            return max(recursive(root.left),recursive(root.right))+1
        if not root:
            return True
        return abs(recursive(root.left)-recursive(root.right))<2 and self.isBalanced(root.left) and self.isBalanced(root.right)

方法二：自底向上的递归

height 函数不仅计算高度，还判断是否平衡。

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def height(root: TreeNode) -> int:
            if not root:
                return 0
            leftHeight = height(root.left)
            rightHeight = height(root.right)
            if leftHeight == -1 or rightHeight == -1 or abs(leftHeight - rightHeight) > 1:
                return -1
            else:
                return max(leftHeight, rightHeight) + 1

        return height(root) >= 0

111. 二叉树的最小深度

广度优先搜索

class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        # 广度优先搜索，队列
        if not root:
            return 0
        dq=deque([(root,1)])
        while dq:
            node,depth=dq.popleft()
            if not node.left and not node.right:
                return depth
            if node.left:
                dq.append((node.left, depth + 1))
            if node.right:
                dq.append((node.right, depth + 1))
        return 0

222. 完全二叉树的节点个数

二分查找

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if not root: return 0
        
        def height(root: Optional[TreeNode]):
            if not root: return 0
            h=0
            while root:
                root=root.left
                h+=1
            return h
        lh,rh=height(root.left),height(root.right)
        if lh==rh:
            return 2**lh + self.countNodes(root.right)
        else:
            return 2**rh + self.countNodes(root.left)

461. 汉明距离

class Solution:
    def hammingDistance(self, x: int, y: int) -> int:
        return bin(x ^ y).count('1')

617. 合并二叉树

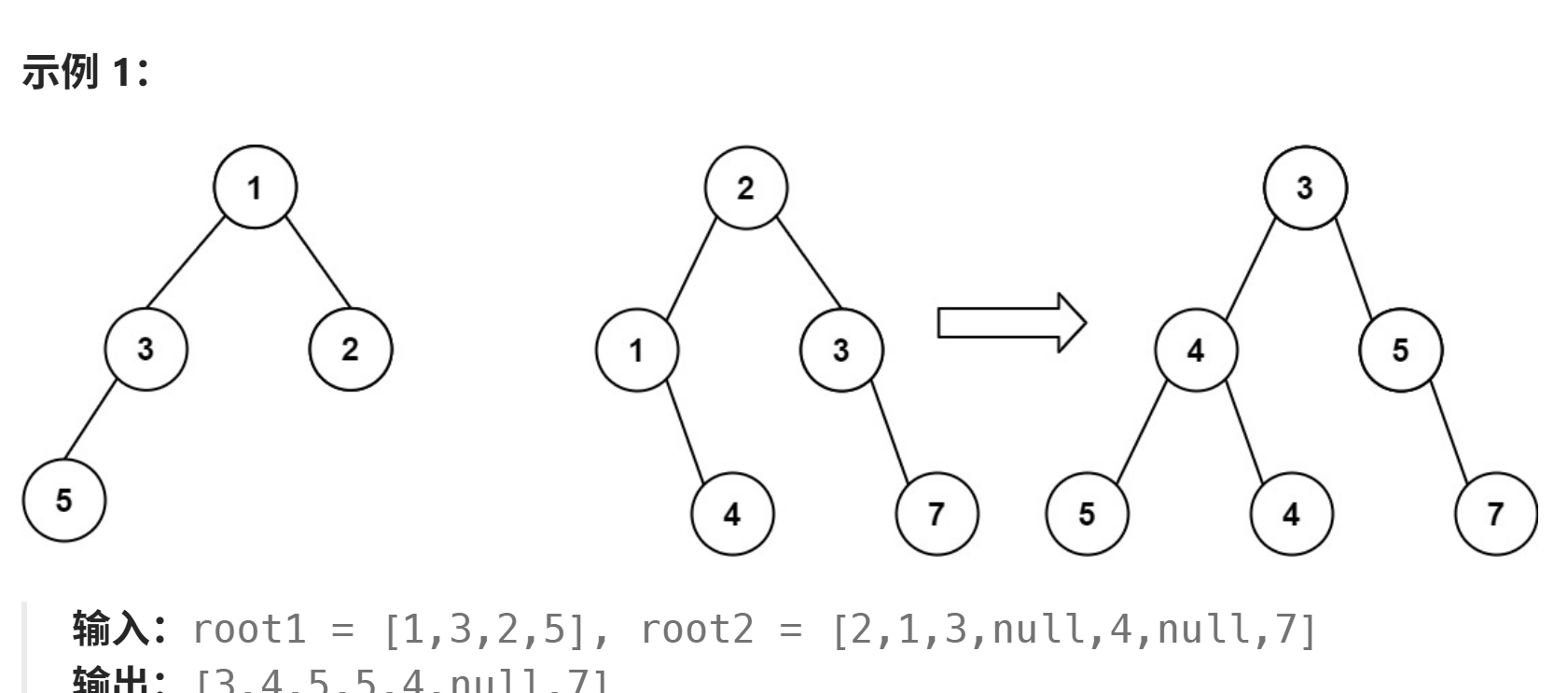
深度

class Solution:
    def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
        if not t1:
            return t2
        if not t2:
            return t1
        
        merged = TreeNode(t1.val + t2.val)
        merged.left = self.mergeTrees(t1.left, t2.left)
        merged.right = self.mergeTrees(t1.right, t2.right)
        return merged

广度

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
        if not t1:
            return t2
        if not t2:
            return t1
        
        merged = TreeNode(t1.val + t2.val)
        queue = collections.deque([merged])
        queue1 = collections.deque([t1])
        queue2 = collections.deque([t2])

        while queue1 and queue2:
            node = queue.popleft()
            node1 = queue1.popleft()
            node2 = queue2.popleft()
            left1, right1 = node1.left, node1.right
            left2, right2 = node2.left, node2.right
            if left1 or left2:
                if left1 and left2:
                    left = TreeNode(left1.val + left2.val)
                    node.left = left
                    queue.append(left)
                    queue1.append(left1)
                    queue2.append(left2)
                elif left1:
                    node.left = left1
                elif left2:
                    node.left = left2
            if right1 or right2:
                if right1 and right2:
                    right = TreeNode(right1.val + right2.val)
                    node.right = right
                    queue.append(right)
                    queue1.append(right1)
                    queue2.append(right2)
                elif right1:
                    node.right = right1
                elif right2:
                    node.right = right2
        
        return merged

938. 二叉搜索树的范围和

class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        if not root:
            return 0
        if root.val > high:
            return self.rangeSumBST(root.left, low, high)
        if root.val < low:
            return self.rangeSumBST(root.right, low, high)
        return root.val + self.rangeSumBST(root.left, low, high) + self.rangeSumBST(root.right, low, high)

被限定了范围，所以用递归找范围，比遍历全部好得多。

953. 验证外星语词典

某种外星语也使用英文小写字母，但可能顺序 order 不同。字母表的顺序（order）是一些小写字母的排列。

给定一组用外星语书写的单词 words，以及其字母表的顺序 order，只有当给定的单词在这种外星语中按字典序排列时，返回 true；否则，返回 false。

class Solution:
    def isAlienSorted(self, words: List[str], order: str) -> bool:
        index = {c: i for i, c in enumerate(order)}
        return all(s <= t for s, t in pairwise([index[c] for c in word] for word in words))

1114. 按序打印

多线程

使用 threading.Event 来确保方法按顺序执行

import threading
 
class Foo:
    def __init__(self):
        self.event1 = threading.Event()
        self.event2 = threading.Event()
 
    def first(self, printFirst: 'Callable[[], None]') -> None:
        printFirst()
        self.event1.set()  # 释放 second 执行
 
    def second(self, printSecond: 'Callable[[], None]') -> None:
        self.event1.wait()  # 等待 first 执行完
        printSecond()
        self.event2.set()  # 释放 third 执行
 
    def third(self, printThird: 'Callable[[], None]') -> None:
        self.event2.wait()  # 等待 second 执行完
        printThird()

使用 threading.Event() 作为同步机制：

event1 确保 second() 在 first() 之后执行。

event2 确保 third() 在 second() 之后执行。

first() 执行后，调用 event1.set() 释放 second()。

second() 通过 event1.wait() 确保 first() 先执行，然后执行 printSecond()，再调用 event2.set() 释放 third()。

third() 通过 event2.wait() 确保 second() 先执行，然后执行 printThird()。

这样可以保证 first() -> second() -> third() 按顺序执行