压控恒流源设计

压控恒流源设计

接地网通常为网格状结构，一般使用镀锌钢焊接制作，网格装内的导体的长度较短，电容、电感效应非常小，在忽略土壤因素的情况下，可以把接地网视为由纯电阻组成的网络。所以在测量计算接地网电阻时可以只考虑其复阻抗的实部。又因为金属导体在交流电流的激励下，易产生涡流和集肤效应，所以在实验系统的电流激励部分选择直流恒流源作为激励源。
恒流源主要由运算放大器、MOS场效应管和基准电阻构成。使用一路运放构成一个正反馈电路控制电压信号和基准电阻的端电压共同作用于MOS场效应管的G极，使MOS场效应管工作在可变电阻区。为了消除电源波动对恒流源的影响，同时能够调整恒流源的输出功率以减小MOS场效应管的发热，在正反馈电路前端添加一个减法电路，将电源电源的波动抵消。电路中TLC2252是一款具有低噪声微功耗等特性的轨对轨运算放大器。IRFB3607PBF是一款N沟道MOSFET，最大关断电压75V，最大导通电流80A，导通电阻仅有9mΩ。为了增大MOS场效应管可变电阻区的变化范围，运算放大器使用12V供电，以获得恒流源更宽的恒流输出能力。电路图如图3-1所示。

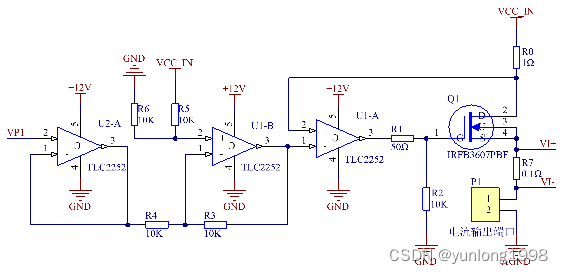
图1 恒流源电路图

U2-A为电压跟随器，一方面作为处理器和后级电路的缓冲，另一方面用于变换阻抗，使处理器的DAC达到最佳的信号输出性能。U1-B为减法器，电源电压减去控制信号电压，以此消除电源电压波动对输出电流的影响。
具体分析如下：设控制信号电压VP1为V_0，电源电压VCC_IN为V_1，减法电路输出端电压为V_2。根据运算放大器虚短、虚断的分析方法，U1-B的正反向输入端电位相等，均为1/2V1，则有:
$$1/2V_1=1/2(V$$