【代码随想录day18】【C++复健】530.二叉搜索树的最小绝对差 ；501.二叉搜索树中的众数 ；236. 二叉树的最近公共祖先

咳咳，小鸽两天出去玩一下，其实昨晚想更新的，但每道题都遇到了若干不好解决的问题，直接把我给绊住了，所以拖到今天更新啦。

530.二叉搜索树的最小绝对差

本题其实只要按卡哥解析里面写的，把树转成vector再来做，其实是非常好做的。

但我此时灵机一动，想到说，如果我能不用到数组，只用前一个值就做出来，岂不美哉？

理论上来说确实是可行的，但一定要想明白一点，那就是中序遍历要怎么传参？如果把前中后序比作在电脑上打开某个窗口并且处理问题，前序就相当于每处理完一个窗口，再新打开一个；后续则是一次性把所有窗口都打开，然后从最新打开的窗口开始慢慢处理。

那么中序呢？它相当于前半段仿照后序遍历，我先把窗口都打开，然后处理完前半段再仿照前序遍历挨个处理节点。但是这也就导致了中序遍历没办法像前后序那样用一种统一的逻辑传参。

我们先来看看前后序遍历是怎么做的：

1 前序遍历：

处理完当前逻辑后，可以通过函数传参的方式传给其左右子树。

2 后序遍历：

处理完当前逻辑后，可以用返回值的方式传给其父节点。

3 中序遍历

坏了，中序怎么办？如果用返回值，前半段逻辑是正确的，后半段逻辑是错的；如果用函数传参，那前半段逻辑就已经错了。那这个时候就只能在外部引用其他变量了，比如类内定义一个叫做pre的变量，或者传参的时候传一个带引用符的参数。这也是为什么在用中序遍历时我们经常见到pre这个变量，以及为什么是以这种方式定义它的原因。

考虑到本题是一个双指针的题目，我又灵机一动，想到说，虽然你的左子树都小于中节点，右子树都大于中节点，那我每次做完差取个绝对值不就好了？这样是不是也不用定义一个外部的pre参数，只要每次同时传当前节点和左右子树节点的指针就行了（简单来说，就是把底下代码的pre前面那个引用号去了，让它变成一个临时变量）？但其实这也是错的。为什么呢？下面举个例子：

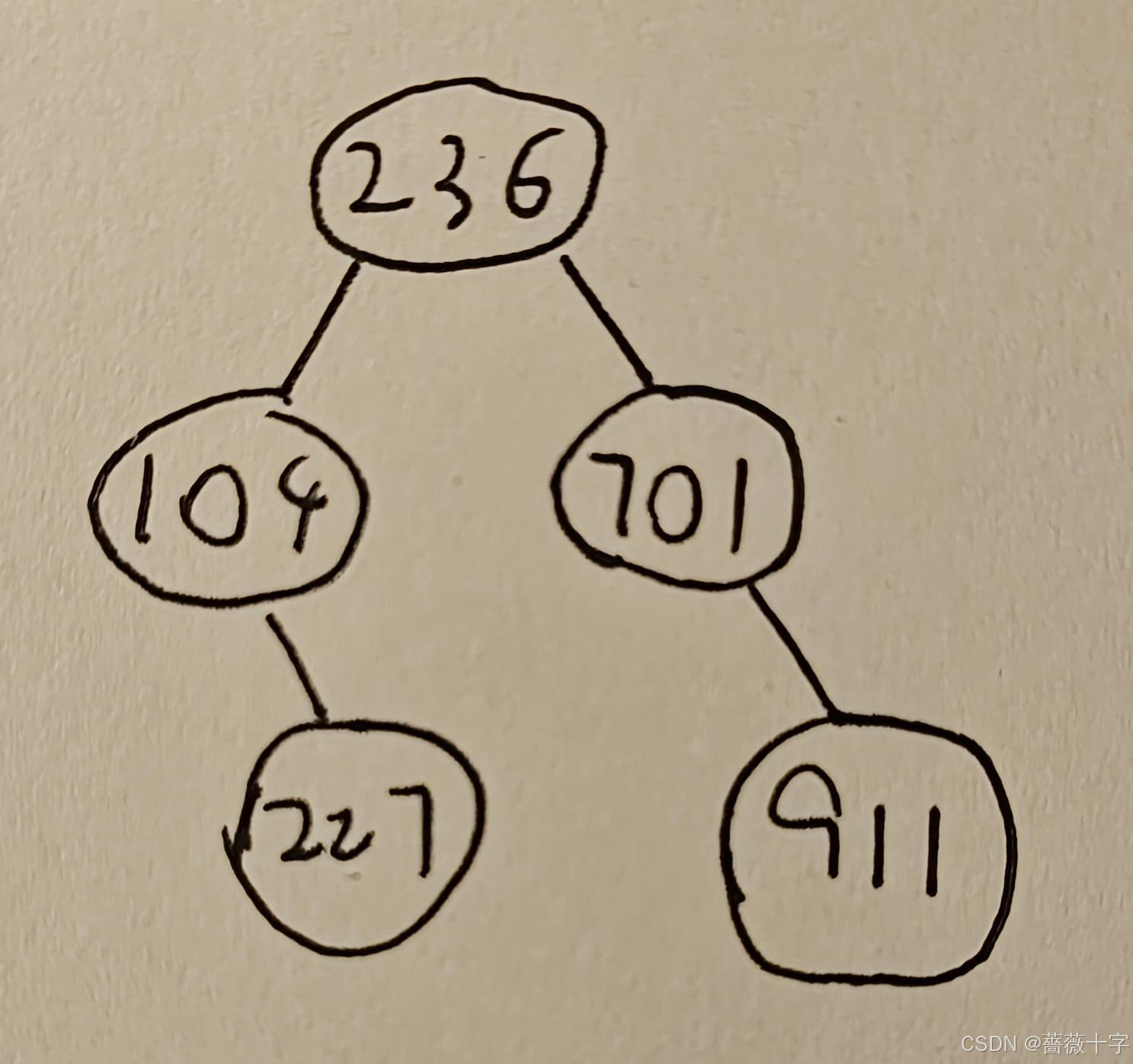
报错的时候我其实还是不太理解，但是一画出来就很明了了：

在不使用外部pre变量的情况下，根节点236无法与左下角节点227比较，从而错失了最小绝对差。也就是说，在中序遍历中，如果不引入外部变量来记录“前一个节点”的状态，就无法实现正确的传值操作。

那么最终与自己和解之后，就能写出如下没有逻辑错误的代码了：

class Solution {
public:
    int getMinimumDifference(TreeNode* root) {
        TreeNode* pre = nullptr;
        int margin = INT_MAX;
        inorder(root, pre, margin);
        return margin;
    }
    void inorder(TreeNode* root, TreeNode*& pre, int& margin){
        if(!root){
            return ;
        }
        inorder(root->left, pre, margin);
        if(pre && abs(root->val - pre->val) < margin){
            margin = abs(root->val - pre->val);
        }
        pre = root;
        inorder(root->right, pre, margin);
    }
};

501.二叉搜索树中的众数

本题来说说实话全忘了。自己一遍也就能写出来一个一般情况的遍历（实际情况是，并非一遍，在建完哈希表之后尬住了）：

class Solution {
public:
    vector<int> findMode(TreeNode* root) {
        unordered_map<int, int> re;
        inorder(root, re);
        int max =0;
        for(const auto& [key, value]:re){
            if(max < value){
                max = value;
            }
        }
        vector<int> result;
        for(const auto& [key, value]:re){
            if(value == max){
                result.push_back(key);
            }
        }
        return result;
    }
    void inorder(TreeNode* root, unordered_map<int, int>& re){
        if(!root){
            return ;
        }
        inorder(root->left, re);
        re[root->val]++;
        inorder(root->right, re);
    }
};

那么在GPT思考之后也是明白了该怎么做，要先遍历一遍找到最大的值，再来一遍找到这些值所对应的索引。（如此看来，这个哈希表也不是非建不可）。

那重头戏肯定是卡哥讲到的第二种直接遍历的方法，这个方法即使是看过解析之后自己做起来还是卡住了，且卡住的理由令人深思：
我发现我和卡哥写得几乎一模一样，但是在一个很特殊的[0, NULL, 0]的情况下，我会返回[0,0]，而卡哥会返回[0]。

在努力观察了7749天后，我发现我和卡哥唯一的区别是卡哥定义pre的方式是定义成了TreeNode*，而我用int存了pre对应的值。

可以简单对比下，这是我的错误代码：

class Solution {
public:
    vector<int> findMode(TreeNode* root) {
        int pre = NULL;
        int maxcount = 0;
        int count = 0;
        vector<int> result;
        inorder(root, result, maxcount, count, pre);
        return result;
    }

    void inorder(TreeNode* root, vector<int>& re, int& maxcount, int& count, int& pre){
        if(!root){
            return ;
        }
        inorder(root->left, re, maxcount, count, pre);
        if(pre && root->val == pre){
            count++;
        }
        else{
            count = 1;
        }
        cout << count << endl;
        cout << maxcount << endl;
        pre = root->val;
        if(count==maxcount){
            re.push_back(root->val);
        }
        else if(count > maxcount){
            maxcount = count;
            re.clear();
            re.push_back(root->val);
        }
        inorder(root->right, re, maxcount, count, pre);
    }
};

这个是最后全过了的代码：

class Solution {
public:
    vector<int> findMode(TreeNode* root) {
        TreeNode* pre = NULL;
        int maxcount = 0;
        int count = 0;
        vector<int> result;
        inorder(root, result, maxcount, count, pre);
        return result;
    }

    void inorder(TreeNode* root, vector<int>& re, int& maxcount, int& count, TreeNode*& pre){
        if(!root){
            return ;
        }
        inorder(root->left, re, maxcount, count, pre);
        if(pre && root->val == pre->val){
            count++;
        }
        else{
            count = 1;
        }
        if(count==maxcount){
            re.push_back(root->val);
        }
        else if(count > maxcount){
            maxcount = count;
            re.clear();
            re.push_back(root->val);
        }
        pre = root;
        inorder(root->right, re, maxcount, count, pre);
    }
};

唯一的区别就是将TreeNode* 改成了int。

聪明的你找到问题了吗？

简单提示一下，问题就出在了这行判断：

if(pre && root->val == pre->val){

那么，谜底揭晓，当pre为int类型且值为0时，上面判断的前半句直接会返回false，也就是说，在上面[0, NULL, 0]的例子中，第二次遍历到0的时候并不会++而是会新添加一个0！

问题找到了，那就是int类的0其实和false是一个意思的。

但不对啊，我之前为了排查这个问题还把这行改了一下：

if(pre != NULL && root->val == pre->val){

但是，这行代码实际上也没法达到我想要的效果！我当时想的是，那你0和NULL不一样，进入当前逻辑并且使得count++。但实际上，这里走的是else分支。为什么呢？

来看GPT的说法：
在 C++ 中，NULL 通常被定义为整数值 0。因此，pre = NULL 实际上等价于 pre = 0。这是因为在早期的 C/C++ 中，NULL 被定义为 #define NULL 0，所以它只是一个 0 的宏定义。

所以，NULL就是0，0就是NULL，当执行上面这行判断且pre=0的时候，pre != NULL会返回false，自动跳过if逻辑并且执行else逻辑。

这...

只能说敲响警钟吧，就像GPT所建议的那样：
在现代 C++ 中，推荐使用 nullptr 而不是 NULL 来表示空指针，这样可以避免 NULL 和 0 混淆的问题。

但其实这样也无法解决int类型的pre初始化问题，因为nullptr只能赋给指针而不能赋给一个int变量，这是不合法的。而GPT给的建议：使用特殊值，也就是用一个特殊的整数值（例如 INT_MIN 或 -1）来表示“未赋值”状态的方法，也会在初始值刚好等于这个值的时候出现问题。

似乎，从最开始用int进行赋值就是一个错误的决定，如果想要完全杜绝这种错误的出现，似乎只能用TreeNode了。

236. 二叉树的最近公共祖先

这个题怎么说呢，虽然的的确确一遍就过了，但是写出来的代码实在太过冗余，这是优化前：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        return postorder(root, p, q);
    }
    TreeNode* postorder(TreeNode* root, TreeNode* p, TreeNode* q){
        if(!root){
            return nullptr;
        }
        TreeNode* left = postorder(root->left, p, q);
        TreeNode* right = postorder(root->right, p, q);
        if(root == p){
            return p;
        }
        else if(root == q){
            return q;
        }
        else{
            if((left == p && right == q) || (left == q && right == p)){
                return root;
            }
            else if(left==p || right ==p){
                return p;
            }
            else if(left==q || right==q){
                return q;
            }
            else if(left!=nullptr){
                return left;
            }
            else if(right!=nullptr){
                return right;
            }
            else{
                return nullptr;
            }
        }
    }
};

这是GPT优化后：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (!root || root == p || root == q) {
            return root;
        }
        
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        
        if (left && right) {
            return root; // p 和 q 分别在左右子树中
        }
        
        return left ? left : right; // 只在左或右子树中找到 p 或 q
    }
};

直接让代码缩短了三倍左右。只能说还是得练。

总结优化点如下：
1 没必要纠结左右子树哪个是p哪个是q，只要有值其实就可以下判断。比如底下这个，如果左右都有值，返回root即可；如果左右单边有值，就返回有值那边的。并且其实这个一句return left?left:right其实还把左右都为空的也涵盖了，这个三目运算符用的真是... 神了。

2 遇到p，遇到q和遇到空的逻辑其实可以并在一起，并且在找到之后就没必要继续往后递归了，我的代码把判断写在了后序遍历后面，其实并没有起到剪枝的作用，并且还很冗余。

只能说这三道题做的真是鸡飞狗跳收获满满！道行还是太浅，好好学吧。