SENet论文总结

SENet简介

       \space\space\space\space\space\space       一般的卷积神经网络，卷积核会融合局部感受野中空间以及通道方向的信息来产生新特征。通过叠加一系列与非线性层和降采样层交织的卷积层，卷积神经网络能够捕获具有全局感受野的层次模式，作为图像的描述。
       \space\space\space\space\space\space       近来一些方法通过强化对特征图空间相关性的学习来增强网络的表达能力，如Inception结构。这篇文章从不同的角度出发 ，通过SE模块对特征图通道之间的相互依赖关系建模来提高网络的表达能力。为了实现这一点，文章提出了一种允许网络对特征图在通道方向上进行自适应重新校准的机制，通过该机制，网络可以学习根据全局信息有选择地强化有用的特征并抑制不太有用的特征。
       \space\space\space\space\space\space       SE(Squeeze-and-Excitation)模块如下图所示。

一个特征图$X\in {\mathbb{R}}^{H^{\prime }\times W^{\prime }\times C^{\prime }}$，经过一系列卷积操作$F_{tr}$，得到特征图$U\in {\mathbb{R}}^{H\times W\times C}$，然后$U$进入SE模块：
1、S(Squeeze)操作：对特征图$U$在空间维度上进行压缩，生成$1\times 1\times C$的特征向量。即对特征图每个通道$H\times W$的空间信息整合为一个实数，这个实数蕴含了对应通道的$H\times W$特征图的全局分布信息。这样使得网络浅层也可以利用全局感受野的信息。
2、E(Excitation)操作：根据通道的依赖关系，基于门机制为每个通道学习特定的权重。
3、reweight操作：将E操作生成的每个通道的权重赋予原输出特征图$U$，作为SE模块的输出。

SENet细节

SE(Squeeze-and-Excitation)模块

       \space\space\space\space\space\space        $F_{tr}$记为一次卷积操作，将输入特征图$X\in {\mathbb{R}}^{H^{\prime }\times W^{\prime }\times C^{\prime }}$转换为输出特征图$U\in {\mathbb{R}}^{H\times W\times C}$。$V=[v_1,v_2,...,v_C]$表示一共有$C$个卷积核。输出特征图有$C$个通道即$U=[u_1,u_2,...,u_C]$。输入特征图有$C^{\prime }$个通道即$X=[x^1,x^2,...,x^{C^{\prime }}]$。$C$个卷积核中第$c$个卷积核可以表示为$v_c=[v_c^1,v_c^2,...,v_c^{C^{\prime }}]$。那么输出中第$c$个通道的特征图$u_c$可以表示为（其中“$\ast$”为卷积操作）
$u_c=v_c\ast X=\sum _{s=1}^{C^{\prime }}{v}_c^s\ast x^s$
卷积操作是将卷积核与特征图在空间维度方向和通道维度方向上的对应元素相乘再求和，那么学习得到的卷积核是隐含有该特征图通道之间的依赖信息的，但这一信息是与特征图空间相关性信息混在一起的。文章的目标是突出特征图通道之间的关系，因为每个通道的特征图含有不同的信息，文章想要使网络对于含有有用信息的那些通道中的特征图更加敏感，而抑制没有包含多少有价值信息的特征图。文章用SE模块来实现这一目标，通过重新校准不同通道的特征图，使网络对于不同通道有不同的响应。

Squeeze操作（全局信息融合）

       \space\space\space\space\space\space       为了判断每个通道中的特征图哪一个含有有用信息，哪一个不包含什么有用的信息，我们希望通过每个通道特征图的整体信息综合判断。然而输出特征图$U$每个像素只包含局部感受野的信息，无法探索更多的上下文信息，这一问题对于浅层更严重，因为浅层特征图每个像素对应的感受野更小。
       \space\space\space\space\space\space       为了得到全局特征信息，文章使用global average pooling，将每个通道的特征图压缩为一个实数，融合了这一通道特征图的全局信息，并将这个实数作为该通道的“标识符”。global average pooling产生一个向量$z\in {\mathbb{R}}^C$，对于第$c$个元素，计算如下：
$z_c=F_{sq}(u_c)=\frac{1}{H\times W}\sum _{i=1}^H\sum _{j=1}^W{u}_c(i,j)$
融合全局信息的方式有很多，文章为了简化问题选择了global average pooling。

Excitation操作（自适应重新校准）

       \space\space\space\space\space\space       Excitation操作利用Squeeze操作整合的各通道信息，提取特征图通道之间的依赖关系。为了实现这一目标，Excitation操作必须满足两个特性：1、Excitation操作必须很灵活（特别是，它必须能够学习通道之间的非线性相互作用）2、它必须学习一种非互斥关系，因为通道之间是有相互依赖关系的，所以我们希望确保多个通道能够同时被激活，而不是一次只激活一个通道。为了实现这些特性，文章选择使用带有sigmoid函数的门机制：
$s=F_{ex}(z,W)=\sigma (g(z,W))=\sigma (W_2\delta (W_{1}z))$
其中$\delta$表示ReLU激活函数，$W_1\in {\mathbb{R}}^{\frac{C}{r}\times C}$和$W_2\in {\mathbb{R}}^{C\times \frac{C}{r}}$表示两个全连接层中的权值，这两层全连接层构成了瓶颈结构：$W_1$作为维度缩减层，将$z$（Squeeze操作产生的特征向量）的维度从$C$减小到了$\frac{C}{r}$，然后用ReLU激活，再通过维度增加层$W_2$，将$z$的维度从$\frac{C}{r}$恢复为$C$，最后再用sigmoid函数激活。
       \space\space\space\space\space\space       Excitation操作产生的$C$维向量与原输出特征图$U$对应通道中的元素逐个相乘，得到的最终特征图作为SE模块的输出。最终输出的第$c$个通道的特征图表示如下：
${\tilde{x}}_c=F_{scale}(u_c,s_c)=s_c\cdot u_c$
其中$\tilde{X}=[{\tilde{x}}_1,{\tilde{x}}_2,...,{\tilde{x}}_C]$表示SE模块最终输出的特征图。$F_{scale}(u_c,s_c)$表示第$c$个通道的特征图$u_c\in {\mathbb{R}}^{H\times W}$与Excitation操作产生的$C$维向量的第$c$个元素$s_c$相乘的结果。

SE模块的应用

       \space\space\space\space\space\space       SE模块很灵活，可以“即插即用”到各种网络中。如下图给出了SE模块嵌入到Inception结构中以及嵌入到ResNet中。

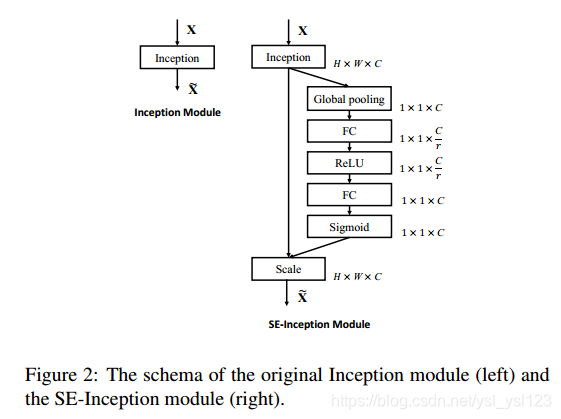
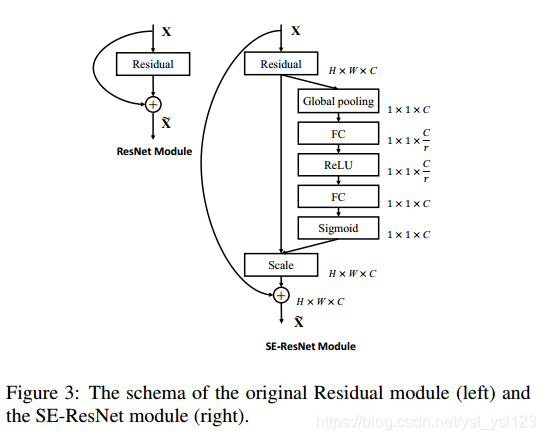
论文地址：Squeeze-and-Excitation Networks