基于DA的低功耗LMS滤波器设计

基于分布式算术的低功耗LMS自适应FIR滤波器设计

1. 引言

在过去的几十年中，由于实现新兴算法的技术日益普及，数字信号处理领域尤其是自适应信号处理得到了极大发展。
这些算法已被广泛应用于各种问题，包括噪声与声学回声消除、信道均衡、信号预测、自适应阵列、无线信道估计、雷达制导系统以及其他许多领域[1]。自适应算法被用于估计时变信号。目前有许多可用的自适应算法，如递归最小二乘（RLS）、卡尔曼滤波器等，但使用最广泛的仍是最小均方（LMS）算法。LMS是一种简单而强大的算法，可利用格型FPGA架构进行实现。其中，权重由著名的维德罗‐霍夫LMS算法[2]更新的抽头延迟线有限冲激响应（FIR）滤波器，因其令人满意的收敛性能[3]，是最为流行的自适应滤波器。然而，FIR滤波器前向路径采用直接形式结构，导致为了计算内积以获得滤波器输出而形成较长的关键路径。因此，当输入信号具有高采样率时，降低结构的关键路径变得至关重要，以免影响系统性能。超过采样周期[4]。基于分布式算术的技术包含一种无乘法器的结构，从而提高了吞吐量。此类基于DA的结构已由阿勒德等人[5]提出。

2. FIR滤波器

有限冲激响应（FIR）滤波器是通信系统中众多信号处理应用的关键组成部分。信道均衡、干扰消除和匹配滤波是FIR滤波器的一些应用领域。因此，下一代通信系统需要可编程和可重构的FIR滤波器架构，这些架构功耗更低、复杂度低并满足高速运行要求。FIR滤波器实现中的主要障碍是乘法器系数的实现，传统上这些系数通过加/减/移位操作来实现。
数字滤波器是数字信号处理系统中的基本单元。传统上，数字滤波器在数字信号处理器（DSP）中实现，但由于其结构本质上是串行的，基于DSP的解决方案无法满足某些应用中的高速要求。如今，现场可编程门阵列（FPGA）技术在数字信号处理领域得到广泛应用，因为基于FPGA的解决方案凭借其并行结构和可配置逻辑能够实现高速运行，从而在整个设计过程以及后续维护中提供极大的灵活性和高可靠性。文献中已报道了多种用于实现涉及正交变换和数字滤波器等DSP算法的基于存储器的实现架构[6]。
FIR滤波器采用乘法器和带反馈的加法器串行实现，其高层示意图如图1所示。

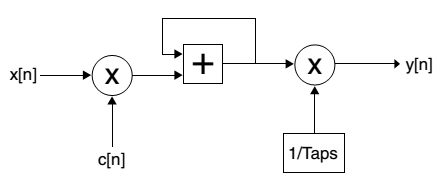
LMS算法以迭代方式更新系数，并将其输入到FIR滤波器。
FIR滤波器随后将该系数c(n)与输入参考信号x(n)结合使用，以生成输出响应y(n)。然后将输出y(n)从期望信号d(n)中减去，以产生误差信号e(n)，该误差信号最终被LMS算法用于计算下一组系数。

3. 自适应FIR滤波器

自适应滤波器可以被理解为一种自修改的数字滤波器，它通过调整其系数以最小化误差函数。该误差函数也称为代价函数，是参考信号（期望信号）与自适应滤波器输出响应之间的距离度量。自适应滤波器能够在未知环境中令人满意地运行，并跟踪输入统计特性的时变特性，这使其成为信号处理和控制应用中的强大工具[7]。面对变化的情况和系统需求的变化，它们能够自动适应（自优化）。它们可以根据某些更新方程被训练来执行特定的滤波和决策任务。此外，由于其具有实时自调整特性，自适应滤波器有时还需跟踪缓慢变化环境下的最优行为。由于结构简单且有效，目前应用最广泛的自适应滤波器结构是与标准有限持续时间脉冲响应（FIR）滤波器相关的横向滤波器（或抽头延迟线）。滤波器结构显著影响给定自适应滤波算法的计算复杂度以及整个自适应过程的总体速度。图2展示了工作在离散时间域k的自适应滤波器的基本结构。在这种结构中，输入信号表示为x(k)，参考或期望信号d(k)（通常包含一定的噪声成分），y(k)是自适应滤波器的输出，误差信号定义为e(k)= d(k)− y(k)。

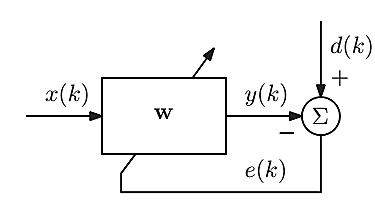
自适应算法利用误差信号，根据某种性能准则来更新自适应滤波器系数向量w(k)。从广义上讲，整个自适应过程的目标是最小化误差信号的某种度量，从而使自适应滤波器输出信号逼近参考信号。

4. LMS自适应滤波器（现有设计)

最小均方（LMS）算法由维德罗和霍夫于1959年提出。
LMS算法之所以成为自适应信号处理的主流方法，主要有两个原因：实现简单，且计算效率与可调参数数量呈线性关系。鲁棒性能
它是一种自适应算法，采用基于梯度的最速下降法。
LMS算法利用从可获得数据中估计出的梯度向量。LMS包含一个迭代过程，沿梯度向量的负方向对权向量进行连续修正，最终达到最小均方误差（MSE）。梯度即德尔算子（偏导数），用于求取表示误差的函数的散度。相对于这种情况下的第n个系数。LMS算法通过采用函数的负梯度来接近函数的最小值，从而最小化误差。

通过调整滤波器系数c(n)来跟踪期望信号d(n)。输入参考信号x(n)是一个已知信号，作为FIR滤波器的输入。d(n)与y(n)之间的差值为误差e(n)。然后将误差e(n)提供给LMS算法，以计算滤波器系数c(n+1)，从而以迭代方式最小化误差。用于计算FIR系数的LMS方程如下：
c(n+1)= c(n)+ µ. e(n). x(n) (1)
where e(n)= d(n) – y(n) (2)
y(n)= cq T (n). x(n) (3)
LMS算法的收敛时间取决于步长μ。
第n次训练迭代时的输入向量x(n)和权向量c(n)分别由以下给出：
x(n)=[x(n), x(n − 1),…, x(n − N+ 1)] T (4)
c(n)=[c0( n), c1( n),…, cN−1( n)] T (5)
d(n)是期望响应， y(n)是第n次迭代的滤波器输出。
e(n)表示在第n次迭代期间计算的误差，用于更新权重，
μ是收敛因子，且 N是滤波器长度。
在流水线架构中，反馈误差e(n)只有在经过一定数量的周期后才可用，该周期数称为自适应延迟。因此，流水线架构使用延迟误差e(n − m)来更新当前权重，而不是使用最新的误差，其中‘m’为自适应延迟。这种延迟最小均方自适应滤波器的权重更新方程由下式给出：
c(n+ 1)= c(n)+ μ · e(n − m) · x(n − m). (6)

5. 分布式算术（DA）

分布式算术（DA）是一种高效的无乘法技术，用于计算内积，最初由Croisier等人[8] 和Zohar[9] 提出，并进一步发展。三十多年前，佩莱德和刘[10]。乘法运算被一种在将乘积累加之前生成部分积的机制所取代。分布式算术与标准乘法的基本区别在于部分积的生成和累加方式。自提出以来，分布式算术已在许多数字信号处理应用中得到广泛实现，包括但不限于数字滤波、离散余弦变换、离散傅里叶变换。

6. 基于分布式算术的方法（所提出的设计）

最小均方自适应滤波器在每个周期内都需要执行内积计算，这部分占据了关键路径的大部分。设公式(3)中的内积为：
(7)
其中，ck和xk （ 0 ≤ k ≤ N − 1 ）分别是对应于当前权重和最近N − 1个输入的N点向量。假设L为权重的位宽，则权向量的每个分量可用二进制补码表示如下：
(8)
其中ckl 表示ck的第l位。
代入(8)式，可将(7)式展开写成如下形式：
(9)
现在，为了将(7)式的积之和形式转换为分布式形式，可以交换(6)式中对索引k和l的求和顺序，得到：
(10)
且由(10)给出的内积可以计算为：
, where (11)

由于N点比特序列{ckl for 0 ≤ k ≤ N − 1 1 l = 0 − 1 2N 2N}中的任意元素只能是零或一，因此对于l，，…，L的每个部分和y可能具有若干种取值。
如果yl的所有可能取值都被预计算并存储在查找表中，则可以使用比特序列{ckl}作为地址位，从查找表中读取部分和yl ，以计算内积。
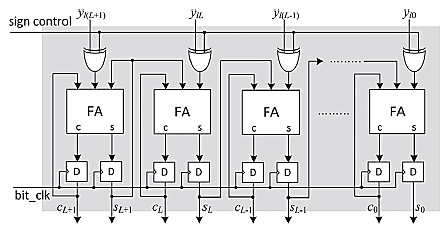
因此，式(11)中的内积可以在L个周期的移位累加中完成计算，随后进行对应于L个比特切片{ckl}的LUT读取操作，其中0 ≤ l ≤ L − 1，如图4所示。由于图4中的移位累加包含较长的关键路径，因此采用进位保存累加器实现，如图5所示。
向量c的比特切片按从最低有效位（LSB）到最高有效位（MSB）的顺序依次送入进位保存累加器。然而，在MSB切片的情况下，需要对LUT输出的负数（补码）进行累加。因此，当MSB切片作为地址出现时，将LUT输出的所有比特通过带有符号控制输入的异或门，且该符号控制输入被设置为‘1’。此时，异或门产生对应于MSB切片的LUT输出的反码，而对其他比特切片的输出不产生影响。
最后，在L个时钟周期后得到的和与进位字必须由一个最终加法器相加（该最终加法器未在图中示出），并且需要将最终加法器的输入进位设置为‘1’，以补偿对应于MSB切片的LUT输出的补码操作。kth LUT存储位置的内容可表示为：
(12)
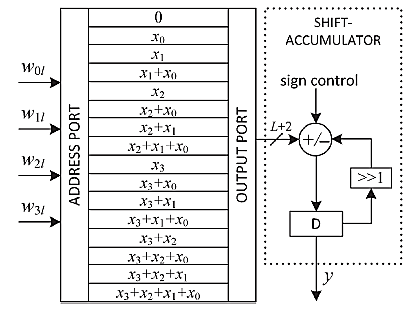
其中，kj是整数k的N位二进制表示中第(j + 1)位的值，0 ≤ k ≤ 2 N − 1。注意，c k （0 ≤ k ≤ 2 N –1）可以预计算并存储在包含2 N 个字的基于RAM的查找表中。然而，我们并未在查找表中存储2 N 2 N − 1 2 N − 1个字，而是将( )个字存储在由寄存器构成的DA表中。图6展示了当N = 4 时此类DA表的一个示例。该表仅使用15个寄存器来存储输入字的预计算和。七个加法器并行计算c k 的新值。

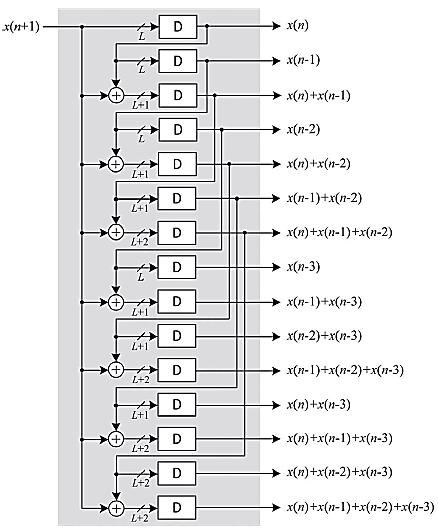
高阶自适应滤波器的计算必须分解为小型自适应滤波模块，因为基于DA的长向量内积实现需要非常大的查找表[5]。
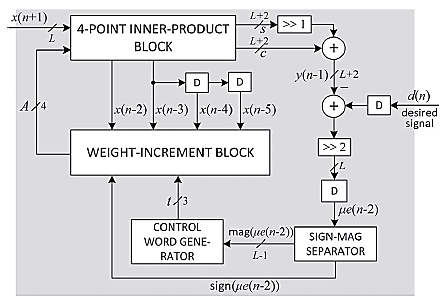
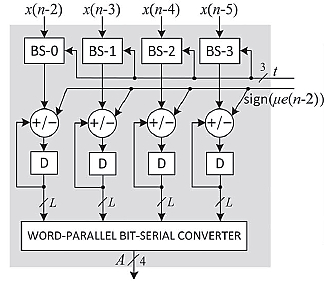
长度为N = 4的基于分布式算术的自适应滤波器的提出结构如图7所示。该结构包含一个四点内积模块和一个权重增量模块，此外还包括用于计算误差值e(n)和桶形移位器控制字t的附加电路。图8]所示的四点内积模块[包括一个由15个寄存器组成的DA表，用于存储部分内积yl （0< l ≤ 15 ），以及一个16:1多路复用器，用于选择这些寄存器中的一个的内容。权重A的位片{w3l w2l w1l w0l }（0 ≤ l ≤ L − 1 ）以从最低有效位到最高有效位顺序作为控制信号输入至多路复用器，多路复用器的输出被送入进位保存累加器（如图4所示）。经过L个位周期后，进位保存累加器对所有部分内积进行移位累加，并生成大小均为(L + 2)位的和字与进位字。进位字和和字被移位——加上输入进位“1”以生成滤波器输出，然后从期望输出 d(n)中减去该滤波器输出，从而得到误差e(n)。与[5],的情况相同，除最高有效位外，误差的所有其他位均被忽略，因此输入xk与误差的乘法通过将误差幅度中的前导零个数所指定的位置数进行右移来实现。计算出的误差幅度被解码以生成用于桶形移位器的控制字t。用于生成桶形移位器控制字t的逻辑如图10所示。收敛因子μ通常取为O(1/N)。此处收敛因子取为 μ= 1/N。然而，也可以将μ取为2−i/N，其中i是一个小整数。在这种情况下，移位次数t增加i，并相应地将桶形移位器的输入预先移动i个位置，以降低硬件复杂度。图9]所示的权重增量单元[（当N = 4时）由四个桶形移位器和四个加法/减法单元组成。桶形移位器将k , , …, N对应的各个输入值x k − 1 = 0 1根据估计误差中最高有效位的位置确定的适当位置数进行移位。桶形移位器产生期望增量，这些增量将被加到或从当前权重中减去。误差的符号位用作加法/减法单元的控制信号，使得当符号位为零或一时，桶形移位器输出分别与权重寄存器中对应当前值的内容相加或相减。

7. 结果

表1：现有工作与本设计在面积、延迟和功耗方面的结果比较

设计	门电路数量	延迟 (nS)	功率 (mW)
现有	31,184	13.704	183
提出	31,500	13.704	91

可以看出，功耗已降低至现有设计的一半以下。这主要是由于基于进位保存加法器的设计减少了开关活动。提出了一种高效的流水线架构，用于低功耗和低延迟的基于分布式算术的自适应滤波器实现。本设计实现了带符号的部分内积的进位保存累加方案，用于滤波器输出的计算。从综合结果中发现，所提出的设计相比我们之前基于分布式算术的FIR自适应滤波器具有更低的功耗。未来的工作可应用于数字通信、信号处理应用、数字无线电接收机、软件无线电接收机以及回声消除等领域。

8. 结论

本文提出了用于计算滤波器输出的带符号部分内积的进位保存累加方案的实现。该方案在自适应滤波应用中得到了良好实现。从综合结果来看，所提出的设计相比我们之前的基于分布式算术的FIR自适应滤波器功耗更低。