周报5_YMK

最新推荐文章于 2025-10-06 06:19:19 发布

原创最新推荐文章于 2025-10-06 06:19:19 发布 · 1k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#学习

部署运行你感兴趣的模型镜像

周报5

论文：FLASHDECODING++: FASTER LARGE LANGUAGE MODEL INFERENCE ON GPUS

https://arxiv.org/pdf/2311.01282.pdf

在斯坦福大学团队的 Tri Dao 等人提出了 FlashAttention 和 FlashDecoding 后，相关的工作又被很快提出，上周来自无问芯穹（Infinigence-AI）、清华大学和上海交通大学的联合团队提出了一种新方法 FlashDecoding++，因为该工作并不是出自FlashAttention 和 FlashDecoding的团队，所以也被叫做野生的 FlashDecoding

Asynchronized Softmax with Unified Maximum Value

回顾上周讲的 FlashDecoding，在 FlashAttention 的基础上引入了新的并行维度：keys/values的序列长度，然而，在每一个块的内部，计算过程还是同步的（主要是局部最大值）。本文发现这种同步操作的开销约为20%。因此，作者希望去除同步操作，也就是独立计算出partial softmax结果。

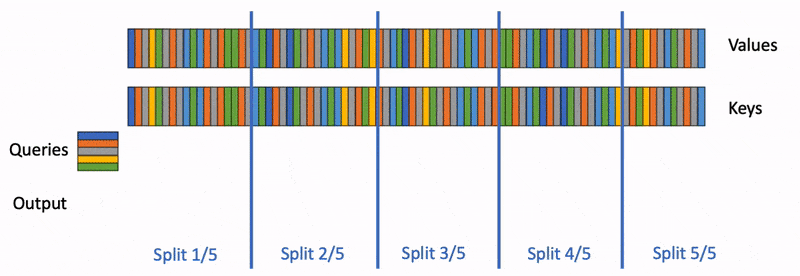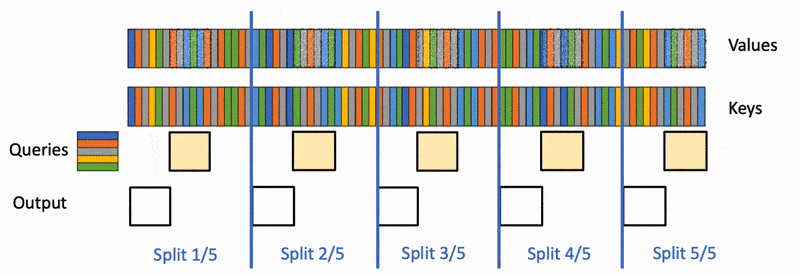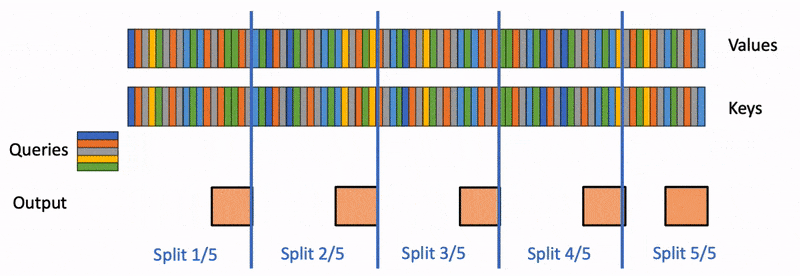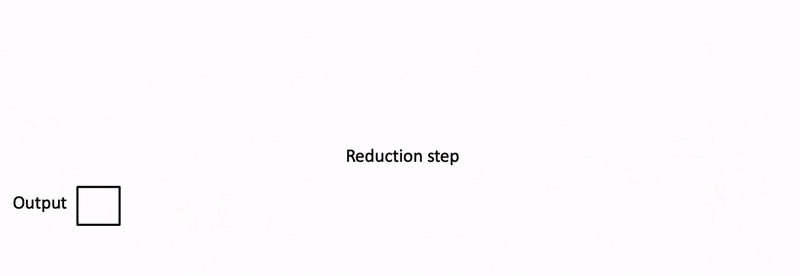
在这里插入图片描述

Softmax的演变:

navie softmax
$y_i=\frac{e^{x_i}}{\sum^V_{i}{e^{x_i}}}$
在这里插入图片描述

safe softmax

由于在实际的计算中，指数计算exp存在不稳定性，比如数值容易溢出，超过一定范围计算精度会下降等问题。因此在实际使用中，往往用safe softmax更好，safe softmax的计算是在navie softmax的基础之上将数组x[1…n]每个元素减去数组的最大值max之后，再做softmax
$y_i=\frac{e^{x_i-max_{k=1}^Vx_k}}{\sum_{j=1}^Ve^{x_j-max_{k=1}^Vx_k}}$
在这里插入图片描述

online softmax

是在safe softmax的基础上做的改进

在这里插入图片描述

其中 $d_{j-1}$ 表示数组x[1…n]的前j-1个指数和，它的指数和是基于前j-1个元素的最大值 $m_{j-1}$ 来算的的，注意哦， $m_{j-1}$ 并不是全局的最大值，同理 $m_{j}$ 表示前j个元素的最大值，那么它跟 $m_{j-1}$ 的区别在于，它有可能等于 $m_{j-1}$ ,也有可能是最新进了的第j个元素 $x_{j}$ .

能看出分块softmax在求的时候依赖于上一个块的max，为了在块的内部也做到并行，作者提出的方法很简单：就是找到一个合适的公共最大值 $ϕ\phi$ 。然而，如果 $ϕ\phi$ 太大，会造成 $e^{{x_i}−ϕ}$ 溢出；如果 $ϕ$ 太小，会造成 $e^{{x_i}−ϕ}$ 精度损失。于是作者进行了统计，如下图所示。例如，对于Llama2-7B， >超过99.99%的值在[-16.8, 6.5]之间。

在这里插入图片描述

但是对于OPT-6.7B来说，其范围较大，于是作者采用动态调整策略，如果在推理过程中发现设置的 $ϕ\phi$ 不合理，那么就终止当前操作，然后采用FlashAttention和FlashDecoding的方法计算softmax。不过怎科学拍出 $ϕ\phi$ 这个数，作者也没给出具体方法。

但是也有人对这个工作表示质疑，一个是 $ϕ\phi$ 的选择是很困难的，极易造成精度的下降，另一个是该优化未必能带来实际的加速。

因为FlashDecoding中：

thread block层次并行度是：sequence_len/block_size
block内thread的并行粒度是：Tile Size，且block_size>Tile Size

在FlashDecoding++中：

thread block层次并行度是：sequence_len/Tile Size
block内thread的并行粒度仍然是：Tile Size

这样不一定对Occupancy（GPU 上同时活跃的线程数量与线程块容量的比率）提升有确定性帮助，如果FlashDecoding的thread block切分比较好把SM沾满，SM内部即使串行计算不同Tile并不一定有什么问题。

Flat GEMM Optimization with Double Buffering

Decoding阶段的过程主要由GEMV（batch size=1）或flat GEMM（batch size>1）。GEMV/GEMM运算可以用M、N、K来表示，其中两个相乘矩阵的大小分别为M × K和K × N。

一般LLM推理引擎利用Tensor Core使用cuBLAS和CUTLASS等库来加速。Tensor Core 在处理矩阵乘法（GEMM）操作时，通常对 M 和 N 的维度有一些优化。当 M 和 N 维度是 8 的倍数时，可以充分发挥其优势。

但是，在解码阶段，可能会执行矩阵向量乘法（GEMV）或扁平化矩阵乘法（Flat GEMM）等操作。在这些特定的操作中，M 的维度可能相对较小，远远小于 64。

由于 Tensor Core 的优化通常期望 M 和 N 的维度是 8 的倍数，所以在解码阶段，如果 M 维度较小，填充零以满足 Tensor Core 期望的维度可能导致计算利用率下降。这是因为填充的零可能占用了矩阵中的大部分空间，而这些零对实际计算没有贡献，从而浪费了计算资源。

若假设N维度上和K维度上的tiling size分别为 $B_N$ 和 $B_K$ ，那么每个GEMM tile的计算量为 $2×M×B_N×B_K$ （这里的2表示乘加2次），总共有 $B=N×KBN×BKB=\frac{N×K}{B_N×B_K}$ 个GEMM tiles。总内存访问量为 $M×B_K+B_N×B_K)×B+M×N$ 。因此，计算和内存比为：

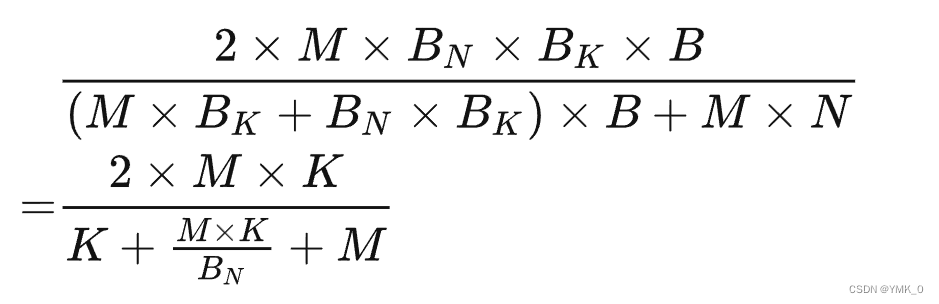
在这里插入图片描述

另一方面，tiling后的并行度是 $N/B_N$ 。

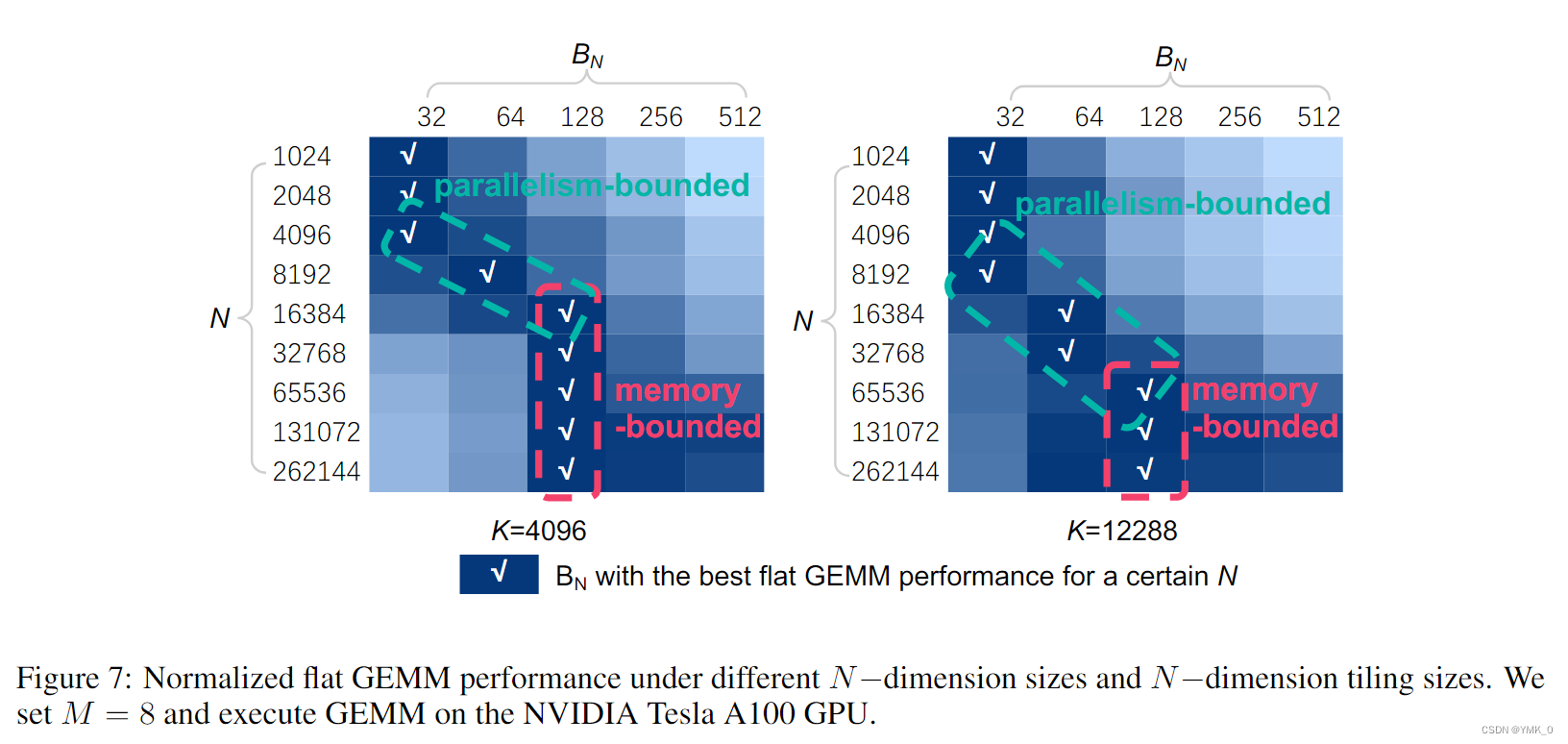
**于是作者发现了：计算和内存比与 $B_N$ 正相关，而并行度与 $B_N$ 负相关。**下图展示了GEMM在不同 $B_N$ 和N下的性能（归一化后）。本文总结了两个关键结论：

当 $N$ 较小时，flat GEMM是parallelism-bounded。NVIDIA Tesla A100中有108个Streaming Multiprocessors (SMs)，于是应该将 $N/B_N$ 设置为一个相关的数（128或256）。
当 $N$ 较大时，flat GEMM是memory-bounded。通过隐藏memory access latency可以提高性能。

为了隐藏memory access latency，本文引入了double buffering技术。具体来说就是在共享内存中分配两个buffer，一个buffer用于执行当前tile的GEMM计算，同时另一个buffer则加载下一个tile GEMM所需的数据。这样计算和内存访问是重叠的，本文在N较大时采取这种策略。

总结：没有FlashAttention和FlashDecoding惊艳，个人觉得FlashDecoding的同步处理代价不大，而且本文中动态调整softmax方法也引入了判断、终止和分支跳转等操作。

ention和FlashDecoding惊艳，个人觉得FlashDecoding的同步处理代价不大，而且本文中动态调整softmax方法也引入了判断、终止和分支跳转等操作。

另外，目前正在看文章 CosmoFlow: Using Deep Learning to Learn the Universe at Scale

您可能感兴趣的与本文相关的镜像

Wan2.2-I2V-A14B

图生视频

Wan2.2

Wan2.2是由通义万相开源高效文本到视频生成模型，是有50亿参数的轻量级视频生成模型，专为快速内容创作优化。支持480P视频生成，具备优秀的时序连贯性和运动推理能力