图论算法——无向图的连通分量

引言

深度优先搜索的一个直接应用就是找出一幅图的所有连通分量。

在深度优先搜索的递归调用期间，只要是某个顶点的可达顶点都能在一次递归调用期间访问到。

有关图的概念可参考博文数据结构之图的概述

连通分量

连通分量：无向图的极大连通子图称为的连通分量( Connected Component)。

极大连通子图说的是，如果将连通分量外的任意一个顶点添加进连通分量都会造成不连通。

比如下图中有四个连通分量

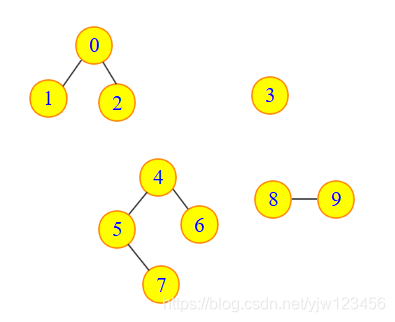
代码

通过id[]标识连通分量，同一连通分量的count值相同,count初始化为0。

for (int s = 0; s < g.vertexNum(); s++) {
   if (!marked[s]) {
        //s的一次递归调用能访问所有与它连通的顶点
        dfs(g,s);
        //到这里说明s的连通顶点已经访问完毕
        count++;
    }
}

实现如下：

package com.algorithms.graph;

import com.algorithms.queue.Queue;

/**
 * 计算无向图的连通分量
 * @author yjw
 * @date 2019/5/22/022
 */
public class CC {
    private boolean[] marked;
    /**
     * 标识连通分量，同一连通分量的值相同
     * 0：第一个连通分量
     * 1：第二个连通分量
     * ...
     *
     * 值为0到count - 1之间
     */
    private int[] id;
    /**
     * 连通分量数
     */
    private int count;

    public CC(Graph g) {
        marked = new boolean[g.vertexNum()];
        id = new int[g.vertexNum()];
        for (int s = 0; s < g.vertexNum(); s++) {
            if (!marked[s]) {
                //s的一次递归调用能访问所有与它连通的顶点
                dfs(g,s);
                //到这里说明s的连通顶点已经访问完毕
                count++;
            }
        }
    }

    private void dfs(Graph g,int v) {
        marked[v] = true;
        id[v] = count;//标识连通分量
        for (int w: g.adj(v)) {
            if (!marked[w]) {
                dfs(g,w);
            }
        }
    }

    public boolean connected(int v,int w) {
        return id[v] == id[w];
    }

    public int id(int v) {
        return id[v];
    }

    public int count() {
        return count;
    }

    @SuppressWarnings("unchecked")
    public void print() {
        System.out.println(count + " components");//count个连通分量

        Queue<Integer>[]components = (Queue<Integer>[]) new Queue[count];
        for (int i = 0; i < components.length; i++) {
            components[i] = new Queue<>();
        }


        for (int i = 0; i < id.length; i++) {
            components[id(i)].enqueue(i);
        }
        for (Queue<Integer> queue : components) {
            System.out.println(queue);
        }

    }

    public static void main(String[] args) {
        Graph g = new Graph(10);
        g.addDiEdges(0,1,2);
        g.addDiEdges(4,5,6);
        g.addEdge(5,7);
        g.addEdge(8,9);

        //System.out.println(g);
        CC cc = new CC(g);
        cc.print();
    }
}

其中Queue和Stack的实现见 栈和队列的实现

我们对示例图计算连通分量，得到输出:

4 components
[0 1 2]
[3]
[4 5 6 7]
[8 9]