B-Tree

B-Tree

B-Tree是一种平衡的多路查找(又称排序)树，在文件系统中和数据库系统中有所应用。主要用作文件的索引。其中的B就表示平衡(Balance) 。
为了描述B-Tree，首先定义一条数据记录为一个二元组[key, data]，key为记录的键值，对于不同数据记录，key是互不相同的；data为数据记录除key外的数据。那么B-Tree是满足下列条件的数据结构：
d为大于1的一个正整数，称为B-Tree的度

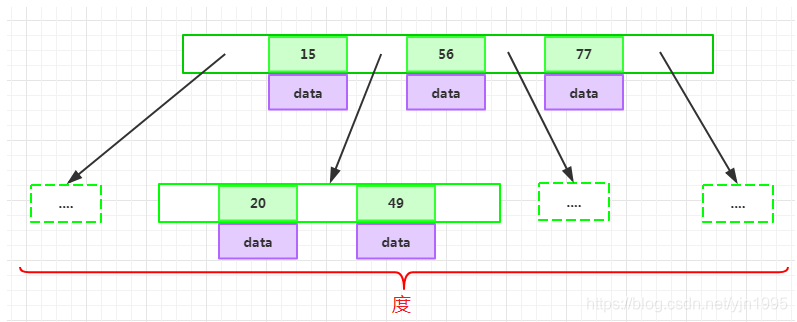
h为一个正整数，称为B-Tree的高度

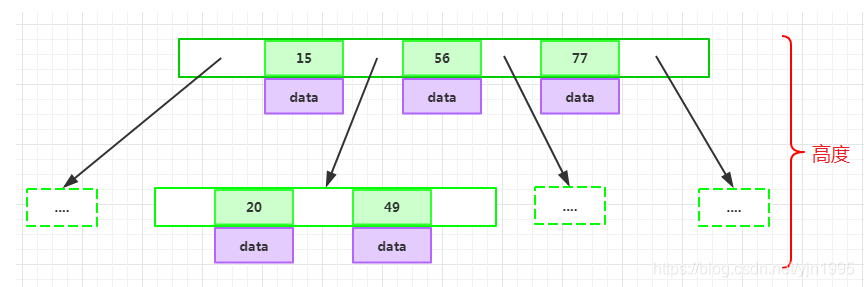
key和指针互相间隔，节点两端是指针

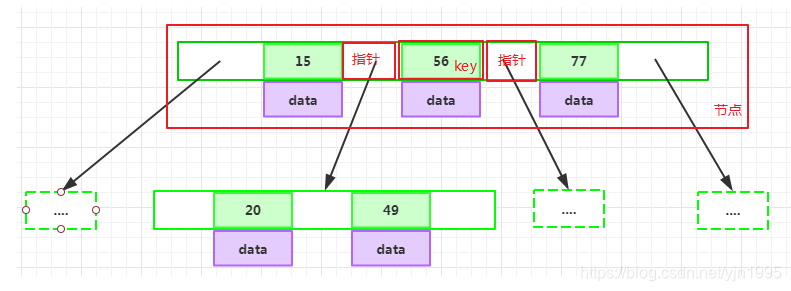
一个节点中的key从左到右非递减排列

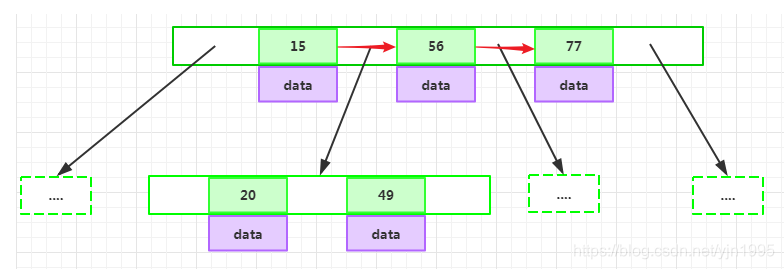
所有节点组成树结构
每个指针要么为null，要么指向另外一个节点
每个非叶子节点由n-1个key和n个指针组成，其中d<=n<=2d

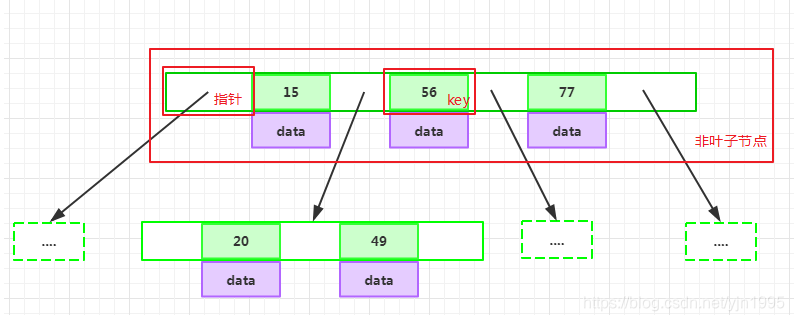
每个叶子节点最少包含一个key和两个指针，最多包含2d-1个key和2d个指针，叶节点的指针均为null

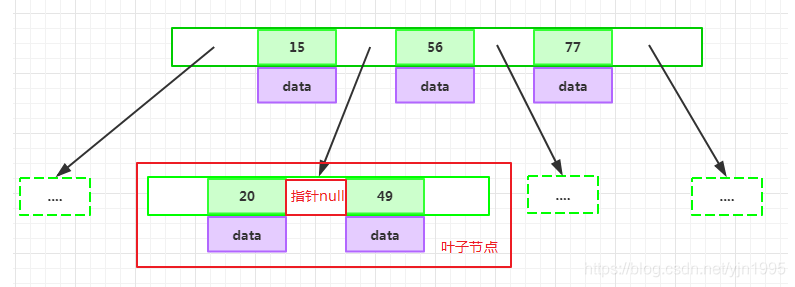
所有叶节点具有相同的深度，等于树高h
如果某个指针在节点node最左边且不为null，则其指向节点的所有key小于key1，其中key1为node的第一个key的值

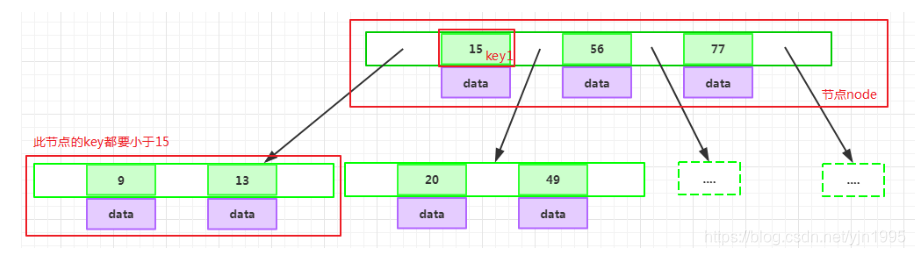
如果某个指针在节点node最右边且不为null，则其指向节点的所有key大于key m，其中key m为node的最后一个key的值

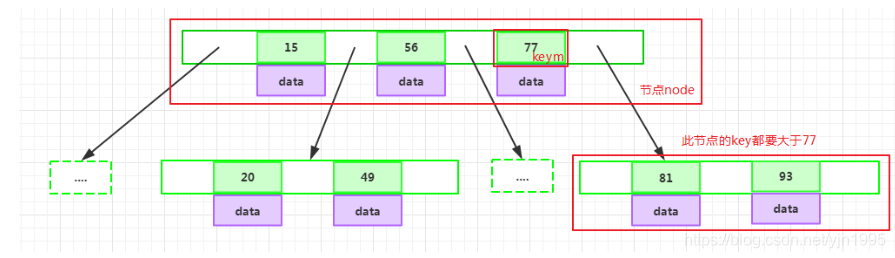
如果某个指针在节点node的左右相邻key分别是key i和key i+1且不为null，则其指向节点的所有key小于key i+1且大于key i

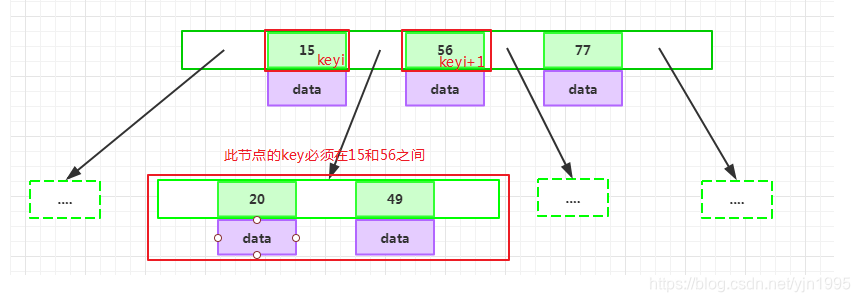
B-Tree是一个非常有效率的索引数据结构。
这主要得益于B-Tree的度可以非常大，高度会变的非常小，只需要二分几次就可以找到数据。
例如一个度为d的B-Tree，设其索引N个key，则其树高h的上限为logd((N+1)/2))，检索一个key，其查找节点个数的渐进复杂度为O(logdN)。

在B-Tree中按key检索数据的算法非常直观：
首先从根节点进行二分查找，如果找到则返回对应节点的data
否则对相应区间的指针指向的节点递归进行查找，如果找到则返回对应节点的data
如果找不到，则重复过程2，直到找到节点或找到null指针，前者查找成功，后者查找失败。