Extending IOU Based Multi-Object Tracking by Visual Information论文简读

写在前面

这篇论文是在方法"High-speed tracking-by-detection without using image information"(IoU)基础上的改进版本，主要解决了前者在检测丢失的情况下，容易出现漏检和身份转换的问题。

贡献

1. 利用一个视觉单目标跟踪器对IoU跟踪器进行扩展，在检测丢失时对跟踪在下一帧的位置进行预测。
2. 提出了一种batch的跟踪方式，有效的减少了IoU跟踪器中的身份转换和跟踪碎片，从而提高IoU跟踪器的MOTA值。

跟踪流程

IoU跟踪流程

我们先回顾一下IoU跟踪器的跟踪流程：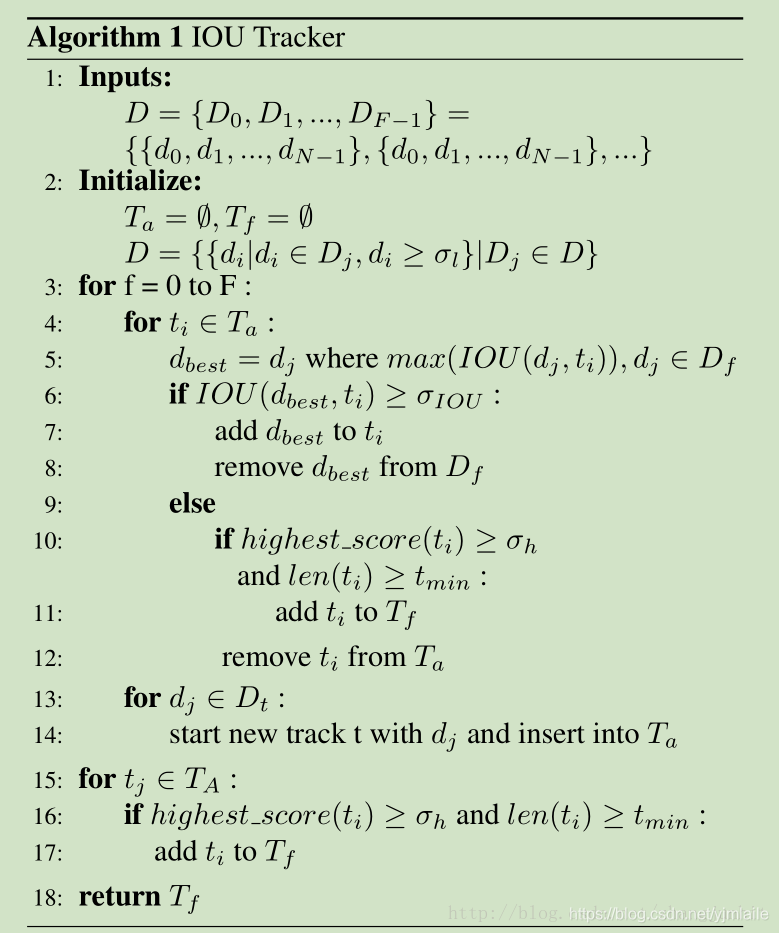

1. 对于当前帧，首先利用阈值${\sigma }_l$对检测进行过滤，得到输入检测集$D$。
2. 对于每个激活跟踪$t_i$，找到与其最后位置IoU最大的检测$d_{best}$，如果满足$IOU(d_{best},t_i)\ge {\sigma }_{IOU}$，将跟踪的最新位置更新为$d_{best}$，将$d_{best}$从检测集$D$中移除。如果不满足$IOU(d_{best},t_i)\ge {\sigma }_{IOU}$，则通过判断跟踪对应检测的最高检测得分是否大于阈值${\sigma }_h$以及跟踪的长度是否大于$t_{min}$，来衡量跟踪$t_i$是否为一个完整的跟踪。如果$t_i$是一个完整的跟踪，则将其添加到完整跟踪列表$T_f$，如果不是则将其终止。将跟踪从激活跟踪$T_a$中移除。
3. 对于没有被匹配的检测，将其初始化为新跟踪并添加到激活跟踪$T_a$中。
4. 在所有帧都按照上述步骤重复完毕后，通过判断激活跟踪$T_a$中每个跟踪对应检测的最高检测得分是否大于阈值${\sigma }_h$以及跟踪的长度是否大于$t_{min}$，来衡量$t_i$是否是一个完整的跟踪。如果是，则将其添加到完成跟踪$T_f$中。

V-IoU扩展

V-IoU跟踪器在IoU跟踪算法的跟踪流程上，添加了一个视觉单目标跟踪器。在主要的跟踪流程中添加一下补充：

1. 在上述步骤2中，对于没有被匹配的跟踪，利用视觉单目标跟踪器进行预测。如果预测成功，利用预测位置作为跟踪在当前帧的位置，将该跟踪添加到激活跟踪中，如果预测失败，判断其是否为一个完整跟踪。在没有检测匹配的情况下，这样一个视觉单目标跟踪过程会持续最大$ttl$帧，如果期间与检测成功匹配，则终止视觉单目标跟踪，利用检测位置更新跟踪位置，直到下一次检测匹配失败。
2. 在检测被初始化为新跟踪后，反向对其进行最大$ttl$帧的视觉单目标跟踪，如果该跟踪与之前的完成跟踪满足时空上的重叠标准，则将两个跟踪进行合并。
3. 对于合并的两条跟踪，删除那些与跟踪距离较远的重叠视觉跟踪。

个人感想

V-IoU跟踪器，也遵循了tracking-by-detection范式，最大的特点是利用单目标跟踪器来进行没有匹配检测跟踪的跟踪预测，这也是未来的多目标跟踪的趋势，在该论文之后的一些多目标跟踪算法中，也都是遵循了这个范式。