Boosting算法与假设间隔

间隔概念

间隔是一种几何度量，能够用于度量分类器预测的可信程度。间隔的两种定义：①样本间隔: 被预测样本与决策面间的距离。支持向量机( support vector machine，SVM) 算法采用了样本间隔概念; ②假设间隔: 要求对分类器之间的距离进行度量，表示在不改变分类结果的前提下分类器可移动的距离，Boosting 算法采用了假设间隔的概念。研究结果表明: ①假设间隔很容易计算; ②假设间隔较大的类别集同样具有较大的样本间隔。图 1 给出了样本间隔和假设间隔的示意

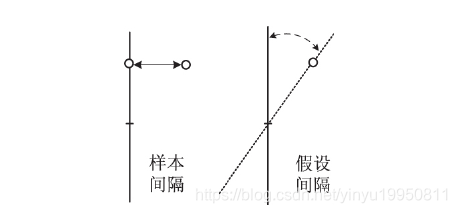
间隔在机器学习中具有重要意义，如果训练分类器的样本具有较大的间隔，则利用该样本训练出的分类器具有较高的置信度，因此一些算法利用最大间隔准则构造评估函数进行特征选择。

AdaBoost算法

Boosting类算法能够提升学习算法的分类准确率，是一种重要的机器学习算法。AdaBoost算法在训练过程中能够对得到的弱分类器错误进行适应性调整，建立互补型分类器组合，提升样本分类预测的准确度。
AdaBoost 算法的主要思想是为训练样本维护分布权重，并根据该权重使弱分类算法关注上一轮中误分类的样本。弱学习算法$h\in H$ 的目标是为分布$D_t$找到一个适当的弱假设 h t : χ → { － 1 ， 1 } h_t: χ→\{ －1，1\} ht​:χ→{－1，1} 。假设数据集中有 m 个样本，初始时 AdaBoost 为每个训练样本赋予相等的权重 1/m，样本 i 在第 t 轮的分布权重表示为$D_t(i)$。弱假设的错误率以式（1）进行度量:
$${ϵ}_t=\sum _{i:h_t(x_i)\ne l_i}{D}_t(i)$$
其中$i:h_t(x_i)\ne l_i$表示仅当样本i错误分类时才取该样本的分布权重。在第$t$轮假设被接受后，算法更新分布$D_t$的权重：
$$D_{t+1}(i)=\frac{D_t(i)exp(-{\alpha }_t{l}_i{h}_t(x_i))}{z_t}$$
$${\alpha }_t=\frac{1}{2}In\frac{1-{ϵ}_t}{{ϵ}_t}$$
$$z_t=\sum _{i=1}^m{D}_t(i)exp(-{\alpha }_t{l}_i{h}_t(x_i))=2\sqrt{{ϵ}_t(1-{ϵ}_t)}$$
其中${\alpha }_t$表示假设$h_t$的投票权重（可信度）。随着$ϵ$的减小$\alpha$将增大，表示弱分类器的可信程度随其错误率的减小而增大。
如果样本被分类正确，则$l_i$和$h_t(x_i)$的符号一致，$D_{t+1}(i)=\frac{D_t(i)exp(-{\alpha }_t)}{z_t}$，否则，$D_{t+1}(i)=\frac{D_t(i)exp({\alpha }_t)}{z_t}$。随着置信度$\alpha$的增大，被正确和错误分类的样本权重$D_t$将分别减小和增大。由于样本被选中的概率由其权重决定，因此后续过程中的弱分类器将以更高的概率处理被错误分类的样本。重复执行$T$次，将产生$T$个弱分类器，将这些弱分类器进行加权组合得到强分类器：
$$H(x_i)=\sum _{t=1}^T{\alpha }_t{h}_t(x_i)$$
在提升弱分类算法过程中，以最小化间隔指数衰减函数的方式构造弱分类器。每一轮训练中被弱分类器误分类样本的权重将会增加，因此 AdaBoost 算法将集中处理难以分类的样本，这种学习过程能够使训练误差上限逐步最小化。在高维数据空间构造弱分类器并不容易，弱分类算法的设计通常基于标量特征，因此 AdaBoost 算法适用于特征选择与分类器的联合设计。

AdaBoost 平均间隔

AdaBoost 具有优良的泛化性能，通常采用间隔分析法对其进行解释。参考资料【2】引入了统计学习中的间隔理论分析其泛化误差，认为间隔可以作为分类器预测能力的度量，如果分类器间隔较大则算法具备良好的泛化能力，间隔较小则泛化能力弱，Schapire 同时给出了 AdaBoost 的泛化误差上界，认为其泛化能力只依赖于间隔分布，且 AdaBoost 所采用的贪心方法具有增大训练样本间隔的能力。与任意实例 i 相关的 AdaBoost 间隔定义:
$$\rho (x_i)=\frac{l_{i}H(x_i)}{w}=\frac{l_i{\sum }_{t=1}^T{\alpha }_t{h}_t(x_i)}{w}$$
其中，$w$表示归一化因子，$w={\sum }_{t=1}^T{\alpha }_t$。假设正确时$l_i$与$h_t(x_i)$ 符号相同，假设错误时两者符号相异，因此可以看出间隔$\rho (x_i)$的取值范围为 $[-1,1]$，并且仅当 $\rho (x_i)>0$ 时样本能够被正确分类。与普通间隔相比，平均间隔能够从统计学角度考虑整体间隔分布。
m个样本的平均间隔$E_s[lH(x_i)]定义为：
$$\bar{\rho }=\frac{1}{m}\sum _{i=1}^m\rho (x_i)=\frac{{\sum }_{i=1}^m{l}_{i}H(x_i)}{mw}=\frac{{\sum }_{i=1}^m{l}_i{\sum }_{t=1}^T{\alpha }_t{h}_t(x_i)}{m{\sum }_{t=1}^T|{\alpha }_t|}=\frac{{\sum }_{i=1}^m{\sum }_{t=1}^T{l}_i{\alpha }_t{h}_t(x_i)}{m{\sum }_{t=1}^T|{\alpha }_t|}$$
根据参考资料【3】的证明，可以归纳出 AdaBoost泛化能力的依赖条件: ①样本大小; ②弱分类器复杂度; ③平均间隔; ④迭代次数。这些因素都会影响 AdaBoost 泛化错误率，其中平均间隔对泛化能力的影响可以描述为：平均间隔越大则泛化能力越强。本文基于平均间隔大小与 AdaBoost 泛化性能成正比的结论，采用了平均间隔概念对特征质量进行评估。

参考资料

1. 基于最大平均间隔的特征选择方法研究
2. How boosting the margin can also boost classifier complexity.
3. The kth，median and average margin bounds for AdaBoost.