万字长文！最全面的大模型Attention介绍，含DeepSeek MLA，含大量图示！

来源: AINLPer 微信公众号（每日论文干货分享！！）
编辑: ShuYini
校稿: ShuYini
时间: 2024-11-24

>>>>专注大模型/AIGC、学术前沿的知识分享！

引言

在深度学习，特别是自然语言处理（NLP）领域，注意力机制（Attention Mechanism）是一个非常重要的概念。Attention机制的起源可以追溯到对生物视觉注意力的模拟以及神经机器翻译的实际需求。Bahdanau等人的工作首次将Attention机制引入自然语言处理领域；而Transformer架构则将Attention机制推向了一个新的高度，使其成为现代自然语言处理的核心技术之一。随着DeepSeek的爆火，它们的MLA注意力方法更是将Attention机制的应用和优化发展到了极致。

Attention机制核心思想是在处理数据时，模型可以有选择性地关注输入的不同部分，进而提升模型的性能。目前，它已经出现了多个升级优化版本，MHA（Mutil Head Attention，多头注意力）、MQA（Mutil Query Attention，多请求注意力）、GQA（Group Query Attention，组请求注意力）、MLA（Multi-Head Latent Attention，多头潜注意力）等。本文将详细介绍这些Attention变体及其实现方法，让你一次性了解当前主流的注意力机制。

视觉注意力

为了方便大家理解，这里简单介绍一下视觉的选择性注意力机制，让大家从主观上有一个大概的理解。视觉注意力机制是人类视觉所特有的大脑信号处理机制。人类视觉通过快速扫描全局图像，获得需要重点关注的目标区域，也就是一般所说的注意力焦点，而后对这一区域投入更多注意力资源，以获取更多所需要关注目标的细节信息，而抑制其他无用信息。

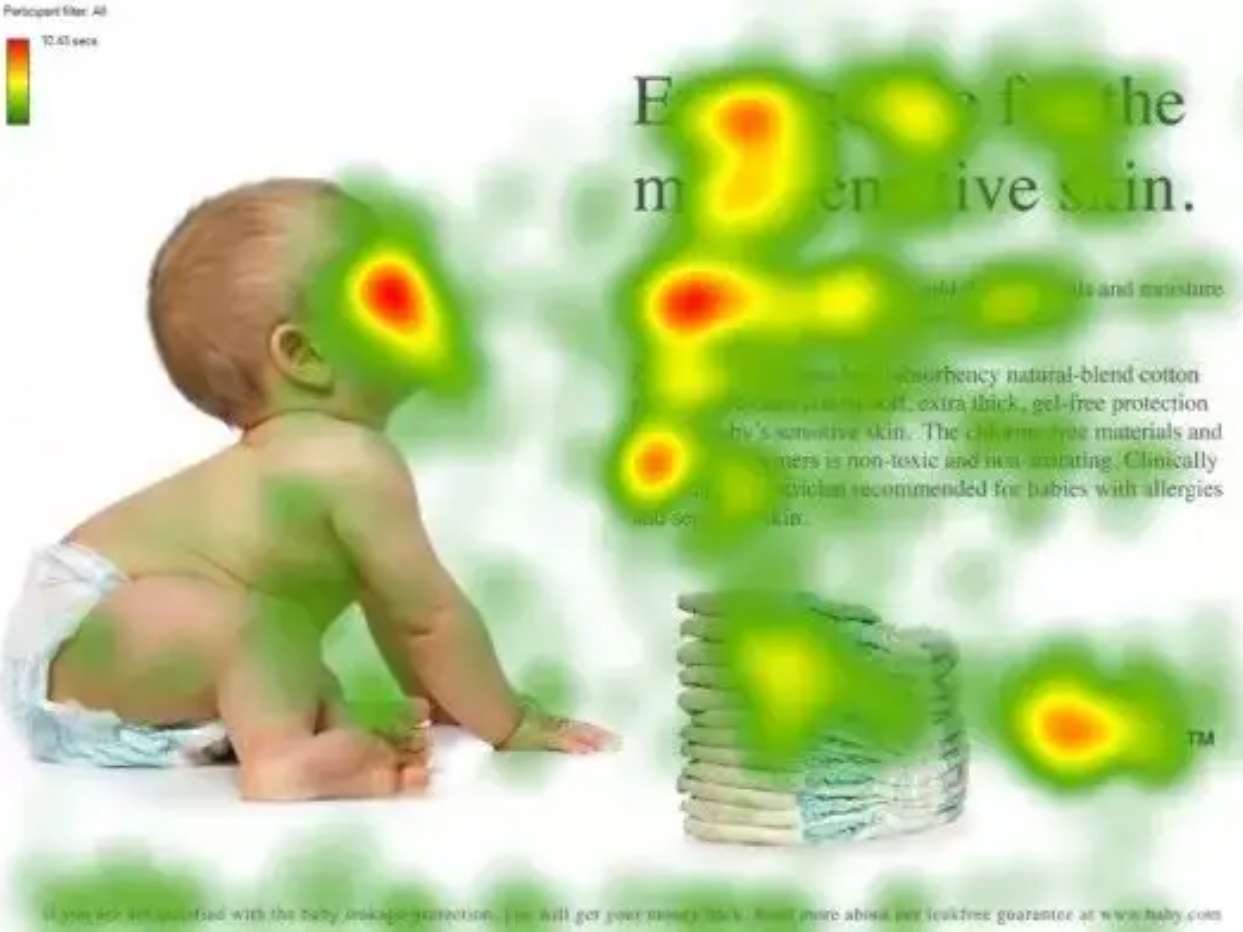
这是人类利用有限的注意力资源从大量信息中快速筛选出高价值信息的手段，是人类在长期进化中形成的一种生存机制，人类视觉注意力机制极大地提高了视觉信息处理的效率与准确性。

上图中展示了人类在看到一副图像时是如何高效分配有限的注意力资源的，其中红色区域表明视觉系统更关注的目标，很明显对于图中所示的场景，人们会把注意力更多投入到人的脸部，文本的标题以及文章首句等位置。

深度学习中的注意力机制从本质上讲和人类的选择性视觉注意力机制类似，核心目标也是从众多信息中选择出对当前任务目标更关键的信息。

在自然语言处理领域，Attention机制最早是为了改善神经机器翻译（NMT）的效果而引入的。传统的神经机器翻译模型基于编码器-解码器架构，使用循环神经网络（RNN）处理序列数据。然而，RNN存在“遗忘”问题，并且在解码过程中无法明确地对齐源语言和目标语言的单词。为此，2014年，Bahdanau等人引入了注意力机制来解决传统神经机器翻译模型的局限性。具体来说，他们在解码过程中为每个输出单词动态计算输入序列中每个单词的重要性权重，从而生成上下文向量，用于生成当前单词。这种方法使模型能够更好地对齐源语言和目标语言的单词，显著提高了翻译质量。

随着2017年Google Brain团队论文《Attention Is All You Need》的爆火，Attention机制在自然语言处理中的重要性得到了进一步提升，论文提出了完全基于Attention机制的Transformer架构，彻底摒弃了传统的循环神经网络结构。Transformer通过自注意力（Self-Attention）机制同时处理序列中的所有单词，并计算它们之间的关系权重，从而能够更高效地处理长距离依赖关系。

Transformer架构的出现可以说是全球人工智能快速发展的转折点，该架构由Encoder和Decoder两部分组成，其中Encoder部分发展成了Bert、Roberta等模型，Decoder部分发展成了GPT等生成式大模型，毫不客气的说，当前我们熟知的生成大模型的模型架构基本上全部都基于Decoder构建的。此类模型效果强悍，并得到了广泛的应用，这进一步推动了Attention机制的发展。

传统注意力机制

单头注意力只使用一个注意力头来计算权重，从而降低计算复杂度，同时保留注意力机制的核心思想。

原理介绍

对于一个输入序列中的某个词，都会与序列中的所有词计算相关性。假设有一个输入序列：
$X=(x_1,x_2,...,x_n)$
对于每个词 $x_i$，我们计算它与所有其他词的相关性，并赋予不同的权重，然后将这些信息进行加权求和，得到新的表示。当前这里的每个词都要在经过Embedding之后，再做权重转换。下面把最经典的Attention计算公式放在这里：
$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

公式对应的流程图如下图所示：

按照上图，这里把Attention计算分成以下几个步骤：

---

(1) 计算 Query, Key, Value 矩阵

每个输入词都会被映射成三个不同的向量：

• $Q$ 是查询（Query），其表示当前需要关注的内容，例如在机器翻译中，查询可能是目标语言句子中的一个词。
• $K$ 是键（Key），表示与查询进行匹配的内容，例如源语言句子中的词。
• $V$ 是值（Value），表示最终要提取的信息，通常与键对应。

定义转换矩阵：
$$Q=X{W}_Q,K=X{W}_K,V=X{W}_V$$
其中，$W_Q,W_K,W_V$ 是可学习的参数矩阵。

---

(2)计算点积

计算查询 $Q$ 和键 $K$ 的点积，得到注意力分数矩阵：
$$\text{scores}=Q{K}^T$$

---

(3)缩放：将点积结果除以 $ \sqrt{d_k} $：其中，$d_k$ 是 Key 向量的维度，$\sqrt{d_k}$ 作为缩放因子，避免数值过大导致梯度消失问题。
KaTeX parse error: Expected 'EOF', got '_' at position 14: \text{scaled_̲scores} = \frac…

---

(4)softmax归一化：对缩放后的点积结果应用softmax函数，得到注意力权重矩阵
KaTeX parse error: Expected 'EOF', got '_' at position 17: …\text{attention_̲weights} = \tex…

---

(5)加权求和：将注意力权重矩阵与值 $V$ 相乘，得到加权求和的结果
KaTeX parse error: Expected 'EOF', got '_' at position 33: …\text{attention_̲weights} \times…

---

示例代码

单头注意力机制代码实现（可直接运行）

import torch
import torch.nn as nn
import torch.nn.functional as F

class SingleHeadAttention(nn.Module):
    def __init__(self, embed_dim):
        """
        单头注意力机制的初始化。
        :param embed_dim: 嵌入维度，Query、Key 和 Value 的维度
        """
        super(SingleHeadAttention, self).__init__()
        self.embed_dim = embed_dim

        # 定义线性层，将输入映射到 Query、Key 和 Value
        self.query_linear = nn.Linear(embed_dim, embed_dim)
        self.key_linear = nn.Linear(embed_dim, embed_dim)
        self.value_linear = nn.Linear(embed_dim, embed_dim)

        # 缩放因子，用于防止点积结果过大
        self.scale = torch.sqrt(torch.FloatTensor($embed_dim]))

    def forward(self, query, key, value):
        """
        单头注意力的前向传播。
        :param query: 查询张量，形状为 $batch_size, seq_len_q, embed_dim]
        :param key: 键张量，形状为 $batch_size, seq_len_k, embed_dim]
        :param value: 值张量，形状为 $batch_size, seq_len_k, embed_dim]
        :return: 输出张量，形状为 $batch_size, seq_len_q, embed_dim]
        """
        # 将输入映射到 Query、Key 和 Value
        Q = self.query_linear(query)
        K = self.key_linear(key)
        V = self.value_linear(value)

        # 计算点积注意力分数
        attention_scores = torch.matmul(Q, K.transpose(-2, -1)) / self.scale

        # 应用 Softmax 函数，得到注意力权重
        attention_weights = F.softmax(attention_scores, dim=-1)

        # 加权求和，得到最终输出
        output = torch.matmul(attention_weights, V)

        return output, attention_weights

# 示例输入
# 假设我们有以下输入张量：
# - query: $batch_size, seq_len_q, embed_dim]
# - key: $batch_size, seq_len_k, embed_dim]
# - value: $batch_size, seq_len_k, embed_dim]
batch_size = 2
seq_len_q = 3 # query的序列长度
seq_len_k = 4 #k,v的序列长度，注意这里K、V是成对存在的
embed_dim = 6 # 假设embedding的维度为6

# 随机生成输入数据
query = torch.randn(batch_size, seq_len_q, embed_dim)
key = torch.randn(batch_size, seq_len_k, embed_dim)
value = torch.randn(batch_size, seq_len_k, embed_dim)

# 初始化单头注意力模块
attention = SingleHeadAttention(embed_dim)

# 前向传播
output, attention_weights = attention(query, key, value)

# 打印输出
print("Query:\n", query)
print("Key:\n", key)
print("Value:\n", value)
print("Output:\n", output)
print("Attention Weights:\n", attention_weights)

MHA–多头注意力

单头注意力中，模型只能通过一个注意力头来捕捉输入数据中的特征，这限制了模型对复杂关系的建模能力。而多头注意力（Multi-Head Attention）是Transformer架构的核心组件，它通过将输入数据分解为多个“头”（heads），分别计算注意力，从而能够捕捉到输入数据中不同子空间的特征。并且对比传统单头注意力，其复杂度并没有增加。这种机制极大地提升了模型对复杂关系的建模能力，广泛应用于自然语言处理（NLP）和计算机视觉（CV）等领域。

原理介绍

多头注意力的核心思想是将输入数据分解为多个子空间，每个子空间通过一个独立的注意力头进行处理，最后将所有头的输出合并起来。相关原理图如下所示：

---

(1) 计算 Query, Key, Value 矩阵

每个输入词都会被映射成三个不同的向量：

• $Q$ 是查询（Query），其表示当前需要关注的内容，例如在机器翻译中，查询可能是目标语言句子中的一个词。
• $K$ 是键（Key），表示与查询进行匹配的内容，例如源语言句子中的词。
• $V$ 是值（Value），表示最终要提取的信息，通常与键对应。

定义转换矩阵：

$$Q=X{W}_Q,K=X{W}_K,V=X{W}_V$$

其中，$W_Q,W_K,W_V$ 是可学习的参数矩阵。可以发现，获取$Q$、$K$、$V$的步骤与前面单头注意力是一样的。

---

(2) 分割多个头

将变换后的查询$Q$、键$K$和值$V$分别分割成多个头。假设我们有 $h$个头，每个头的维度为 $d_k$，则有：

$$d_k=\frac{d_{\text{dim}}}{h}$$

其中，$d_{\text{dim}}$是模型的嵌入维度。

分割后的查询、键和值分别如下，其中，$i$ 表示第 $i$个头。
$$\begin{array}{rl}{\text{Q}}_i& =\text{split}(\text{Q},i)\\ {\text{K}}_i& =\text{split}(\text{K},i)\\ {\text{V}}_i& =\text{split}(\text{V},i)\end{array}$$

---

(3)计算每个头的注意力

对于每个头，分别计算注意力分数。具体步骤如下：

1. 计算点积注意力分数：
   $${\text{Attention Score}}_i={\text{Q}}_i\times {\text{K}}_i^T$$
2. 缩放：
   $${\text{Scaled Score}}_i=\frac{{\text{Attention Score}}_i}{\sqrt{d_k}}$$
   缩放因子 $\sqrt{d_k}$ 的作用是防止点积结果过大导致梯度消失。
3. Softmax：
   KaTeX parse error: Expected 'EOF', got '_' at position 17: …\text{Attention_̲Weights}_i = \t…
   将缩放后的分数转换为概率分布。
4. 加权求和：
   KaTeX parse error: Expected 'EOF', got '_' at position 35: …\text{Attention_̲Weights}_i \tim…

---

(4)合并所有头的输出

将所有头的输出合并起来，得到最终的输出。合并后的输出再通过一个线性变换：
$$\text{Output}=\text{concat}({\text{Output}}_1,{\text{Output}}_2,\dots ,{\text{Output}}_h)\cdot W^O$$
其中，$W^O$是另一个可学习的权重矩阵，用于将合并后的输出映射回原始维度。

---

图文理解

1、首先假设一个输入，该输入seq len为4，hidden_size的维度为8，使用2头注意力；同时弱化batch size（假设为1并且不在维度上体现）。如下图所示：

2、对于已经计算得到的QKV，分别计算attention，最终得到了attention的结果，一个$2\ast 4\ast 4$矩阵（$headnumber\ast seqlen\ast eachheadhiddensize$）

3、获取到了attention的结果后，再经过变换，重新拼接回一个$8\ast 4（hiddensize\ast seqlen）$矩阵。得到拼接后的8*4矩阵后，经过$W_O$，得到$O$矩阵，即输出。

示例代码

import torch
import torch.nn as nn
import torch.nn.functional as F

class MultiHeadAttention(nn.Module):
    def __init__(self, embed_dim, num_heads):
        """
        多头注意力机制的初始化。
        :param embed_dim: 嵌入维度
        :param num_heads: 头的数量
        """
        super(MultiHeadAttention, self).__init__()
        self.embed_dim = embed_dim
        self.num_heads = num_heads
        self.head_dim = embed_dim // num_heads

        assert self.head_dim * num_heads == embed_dim, "Embed size needs to be divisible by heads"

        # 定义线性层，将输入映射到 Query、Key 和 Value
        self.query_linear = nn.Linear(embed_dim, embed_dim)
        self.key_linear = nn.Linear(embed_dim, embed_dim)
        self.value_linear = nn.Linear(embed_dim, embed_dim)

        # 定义输出的线性层
        self.out = nn.Linear(embed_dim, embed_dim)

        # 缩放因子
        self.scale = torch.sqrt(torch.FloatTensor([self.head_dim]))

    def forward(self, query, key, value):
        """
        多头注意力的前向传播。
        :param query: 查询张量，形状为 [batch_size, seq_len_q, embed_dim]
        :param key: 键张量，形状为 [batch_size, seq_len_k, embed_dim]
        :param value: 值张量，形状为 [batch_size, seq_len_k, embed_dim]
        :return: 输出张量，形状为 [batch_size, seq_len_q, embed_dim]
        """
        batch_size = query.shape[0]

        # 将输入映射到 Query、Key 和 Value
        Q = self.query_linear(query)  # [batch_size, seq_len_q, embed_dim]
        K = self.key_linear(key)      # [batch_size, seq_len_k, embed_dim]
        V = self.value_linear(value)  # [batch_size, seq_len_k, embed_dim]

        # 分割成多个头
        Q = Q.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)  # [batch_size, num_heads, seq_len_q, head_dim]
        K = K.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)  # [batch_size, num_heads, seq_len_k, head_dim]
        V = V.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)  # [batch_size, num_heads, seq_len_k, head_dim]

        # 计算点积注意力分数
        attention_scores = torch.matmul(Q, K.transpose(-2, -1)) / self.scale  # [batch_size, num_heads, seq_len_q, seq_len_k]

        # 应用 Softmax 函数，得到注意力权重
        attention_weights = F.softmax(attention_scores, dim=-1)  # [batch_size, num_heads, seq_len_q, seq_len_k]

        # 加权求和，得到每个头的输出
        output = torch.matmul(attention_weights, V)  # [batch_size, num_heads, seq_len_q, head_dim]

        # 合并所有头的输出
        output = output.transpose(1, 2).contiguous().view(batch_size, -1, self.embed_dim)  # [batch_size, seq_len_q, embed_dim]

        # 通过输出的线性层
        output = self.out(output)  # [batch_size, seq_len_q, embed_dim]

        return output, attention_weights

# 示例输入
batch_size = 2
seq_len_q = 3
seq_len_k = 4
embed_dim = 16
num_heads = 4

# 随机生成输入数据
query = torch.randn(batch_size, seq_len_q, embed_dim)
key = torch.randn(batch_size, seq_len_k, embed_dim)
value = torch.randn(batch_size, seq_len_k, embed_dim)

# 初始化多头注意力模块
attention = MultiHeadAttention(embed_dim, num_heads)

# 前向传播
output, attention_weights = attention(query, key, value)

# 打印输出
print("Query:\n", query)
print("Key:\n", key)
print("Value:\n", value)
print("Output:\n", output)
print("Attention Weights:\n", attention_weights)

承上启下–KV Cache

原理介绍

大模型在解码基本上都是通过自回归的方式进行。即：最新的Token输出依赖于先前生成或者预先填入的Token。举个例子，假如我们输入“窗前明月光下一句是”，那么模型每次生成一个token，输入输出会是这样（方便起见，默认每个token都是一个字符，其中[BOS]和[EOS]分别是起始符号和终止符号）。

step0: 输入=[BOS]窗前明月光下一句是；输出=疑
step1: 输入=[BOS]窗前明月光下一句是疑；输出=是
step2: 输入=[BOS]窗前明月光下一句是疑是；输出=地
step3: 输入=[BOS]窗前明月光下一句是疑是地；输出=上
step4: 输入=[BOS]窗前明月光下一句是疑是地上；输出=霜
step5: 输入=[BOS]窗前明月光下一句是疑是地上霜；输出=[EOS]

仔细想一下，在生成“疑”字的时候，用的是输入序列中“是”字的最后一层hidden state，通过最后的分类头预测出来的。以此类推，后面每生成一个字，使用的都是输入序列中最后一个字的输出。可以注意到，下一个step的输入其实包含了上一个step的内容，而且只在最后面多了一点点（一个token）。那么下一个step的计算应该也包含了上一个step的计算。从公式上来看是这样的：

---

1、Attention 计算公式：
$${\alpha }_{i,j}=\text{softmax}(q_i{k}_j^{\top })$$
$$o_i=\sum _{j=0}^i{\alpha }_{i,j}{v}_j$$
注意对于decoder的时候，由于mask attention的存在，每个输入只能看到自己和前面的内容，而看不到后面的内容。

---

2、假设当前输入的长度是3，预测第4个字，那每层attention所做的计算有

$ o_0 = \alpha_{0,0} v_0 $
$ o_1 = \alpha_{1,0} v_0 + \alpha_{1,1} v_1 $
$ o_2 = \alpha_{2,0} v_0 + \alpha_{2,1} v_1 + \alpha_{2,2} v_2 $

---

3、预测完第4个字，放到输入里，继续预测第5个字，每层attention所做的计算有:

$ o_0 = \alpha_{0,0} v_0 $
$ o_1 = \alpha_{1,0} v_0 + \alpha_{1,1} v_1 $
$o_2 = \alpha_{2,0} v_0 + \alpha_{2,1} v_1 + \alpha_{2,2} v_2 $
$ o_3 = \alpha_{3,0} v_0 + \alpha_{3,1} v_1 + \alpha_{3,2} v_2 + \alpha_{3,3} v_3 $

---

可以看到，在预测第5个字时，只有最后一步引入了新的计算，而 o0 到 o2 的计算和前面是完全重复的。但是模型在推理的时候可不管这些，无论你是不是只要最后一个字的输出，它都把所有输入计算一遍，给出所有输出结果。也就是说中间有很多我们用不到的计算，这样就造成了浪费。

图文理解

公式理解不了没关系，再来个图文理解。由于decoder是causal的（即，一个token的注意力attention只依赖于它前面的token），在每一步生成过程中，我们实际上是在重复计算相同的前一个token的注意力，而我们真正需要做的是仅计算新token的注意力。这就是KV cache发挥作用的地方。

通过缓存之前的$k$和$v$，我们可以专注于只计算新token的注意力。以下是每个Token的Attention分数的计算过程，可以发现，$ste{p}_i$相比$ste{p}_{i-1}$，之前的Attention score是不变的，那么一个新的tokne进来，只需要计算当前token对应的kv就可以 了，后面直接拼起来就好了。这里能做kv cache的主要原因是由于mask矩阵的作用，这就是causal模型的先天优势。

Key向量缓存 我们可以像下面这样将其形象化，其中空的方块代表我们可以从以前的迭代中重用的计算部分：

由此我们可以看出，只需要最后一个查询向量和所有关键向量即可计算注意力得分矩阵的最后一行。关键向量本身是通过将输入嵌入乘以关键层权重来计算的，正如我们之前所见：

因此，在每次迭代中，我们只需要计算最后一个键向量（因为这取决于最新标记的输入嵌入），而所有其他键向量都可以从上一次迭代中重复使用。

我们可以通过维护一个密钥缓存来节省大量冗余计算，该缓存存储在每次迭代中计算的键向量。首先，我们只计算一个查询向量和一个键向量：

然后，我们从密钥缓存中提取先前计算的密钥向量，并计算注意力分数矩阵的最后一行作为新查询向量与每个密钥向量的点积：

到目前为止，我们已经了解了缓存关键向量如何消除文本生成循环每次迭代中冗余的注意力得分计算。多头自注意力中的值向量也可以在每次迭代中缓存。

回想一下，值向量是通过将输入嵌入发送到第三个线性层来计算的：

然后，我们通过将两个矩阵相乘来根据注意力得分“重新加权”价值向量：

与键向量一样，每次迭代时只需要计算最后一个（即最新的）值向量。所有其他值向量都可以从值缓存中提取并重复使用：

实际例子

假设我们的 ( Q, K, V ) 分别如下：
$$Q=\left[\begin{array}{cccc}0.212& 0.04& 0.63& 0.36\\ 0.1& 0.14& 0.86& 0.77\\ 0.31& 0.36& 0.19& 0.72\end{array}\right],K=\left[\begin{array}{cccc}0.31& 0.84& 0.963& 0.57\\ 0.45& 0.94& 0.73& 0.58\\ 0.36& 0.83& 0.1& 0.38\end{array}\right],V=\left[\begin{array}{cccc}0.36& 0.83& 0.1& 0.38\\ 0.31& 0.36& 0.19& 0.72\\ 0.31& 0.84& 0.963& 0.57\end{array}\right]$$
在计算完 $\frac{Q{K}^T}{\sqrt{d_k}}$ 得到 attention 矩阵后，我们创建一个 masking 矩阵（其中$-1e9$一个极小值），将其与 attention 矩阵相加：
$$M=\left[\begin{array}{ccc}0& 1& 1\\ 0& 0& 1\\ 0& 0& 0\end{array}\right]\times -1e9=\left[\begin{array}{ccc}0& -1e9& -1e9\\ 0& 0& -1e9\\ 0& 0& 0\end{array}\right]$$
 
$$
\frac{QK^T}{\sqrt{d_k}} + M =
\begin{bmatrix}
0.455605 & 0.40085 & 0.15466 \
0.70784 & 0.6255 & 0.2654 \
0.495935 & 0.5171 & 0.3515
\end{bmatrix}
+
\begin{bmatrix}
0 & -1e9 & -1e9 \
0 & 0 & -1e9 \
0 & 0 & 0 \
\end{bmatrix}

\begin{bmatrix}
0.455605 & -1e9 & -1e9 \
0.70784 & 0.6255 & -1e9 \
0.495935 & 0.5171 & 0.3515 \
\end{bmatrix}
KaTeX parse error: Can't use function '$' in math mode at position 37: …，将这些值转换为概率分布。将 $̲softmax$ 应用于注意力…
softmax \left(
\begin{bmatrix}
0.455605 & -1e9 & -1e9 \
0.70784 & 0.6255 & -1e9 \
0.495935 & 0.5171 & 0.3515 \
\end{bmatrix}
\right)

\begin{bmatrix}
1.0 & 0 & 0 \
0.520573 & 0.479427 & 0 \
0.346392 & 0.353802 & 0.299806 \
\end{bmatrix}
KaTeX parse error: Can't use function '$' in math mode at position 11: 再来看一下不存储 $̲Q$ 的情况，仅存储 $K, …
Q_1 =
\begin{bmatrix}
0.212 & 0.04 & 0.63 & 0.36 \
& - & - & - \
& - & - & - \
\end{bmatrix}
,
Q_2 =
\begin{bmatrix}
& - & - & - \
0.1 & 0.14 & 0.86 & 0.77 \
& - & - & -
\end{bmatrix}
,
Q_3 =
\begin{bmatrix}
& - & - & - \
& - & - & - \
0.31 & 0.36 & 0.19 & 0.72
\end{bmatrix}
KaTeX parse error: Expected 'EOF', got '&' at position 2: &̲ensp; K_1 = \begin{bmatrix} 0.31 & 0.84 & 0.963 & 0.57 \ - & - & - & - \ - & - & - & - \ \end{bmatrix} , K_2 = \begin{bmatrix} 0.31 & 0.84 & 0.963 & 0.57 \ 0.45 & 0.94 & 0.73 & 0.58 \ - & - & - & - \ \end{bmatrix} , K_3 = \begin{bmatrix} 0.31 & 0.84 & 0.963 & 0.57 \ 0.45 & 0.94 & 0.73 & 0.58 \ 0.36 & 0.83 & 0.1 & 0.38 \end{bmatrix} $$

$$V_1=\left[\begin{array}{cccc}0.36& 0.83& 0.1& 0.38\\ -& -& -& -\\ -& -& -& -\end{array}\right],V_2=\left[\begin{array}{cccc}0.36& 0.83& 0.1& 0.38\\ 0.31& 0.36& 0.19& 0.72\\ -& -& -& -\end{array}\right],V_3=\left[\begin{array}{cccc}0.36& 0.83& 0.1& 0.38\\ 0.31& 0.36& 0.19& 0.72\\ 0.31& 0.84& 0.963& 0.57\end{array}\right]$$

$$\frac{Q_1{K}_1^T}{\sqrt{d_k}}=\left[\begin{array}{ccc}0.455605& -& -\\ -& -& -\\ -& -& -\end{array}\right],\frac{Q_2{K}_2^T}{\sqrt{d_k}}=\left[\begin{array}{ccc}-& -& -\\ 0.70784& 0.6255& -\\ -& -& -\end{array}\right],\frac{Q_3{K}_3^T}{\sqrt{d_k}}=\left[\begin{array}{ccc}-& -& -\\ -& -& -\\ 0.495935& 0.5171& 0.3515\end{array}\right]$$
相加后的结果与存储 $ Q $时 masking 的结果相同：
$$\frac{Q_1{K}_1^T}{\sqrt{d_k}}+\frac{Q_2{K}_2^T}{\sqrt{d_k}}+\frac{Q_3{K}_3^T}{\sqrt{d_k}}=\left[\begin{array}{ccc}0.455605& -& -\\ 0.70784& 0.6255& -\\ 0.495935& 0.5171& 0.3515\end{array}\right]$$

应用$softmax$:
$$softmax\left(\left[\begin{array}{ccc}0.455605& -& -\\ 0.70784& 0.6255& -\\ 0.495935& 0.5171& 0.3515\end{array}\right]\right)=\left[\begin{array}{ccc}1.0& -& -\\ 0.520573& 0.479427& -\\ 0.346392& 0.353802& 0.299806\end{array}\right]$$
可以观察到，与存储 $Q$ 时的结果是一致的，这也代表在接下与$V$矩阵计算得到的 Attention 结果也将一样，这也就是为什么我们在 KV Cache 时不需要存储 $Q $ 的原因。

KV Cache 在哪里使用？

当每生成一个新的 token 就会把这个新的 token append 进之前的序列中，在将这个序列当作新的输入进行新的 token 生成，直到$eo{s}_{t}oken$ 结束。这使得每次新序列输入时都需要取重复计算前面的 $(n-1)$个 token 的 $(q,k,v)$，浪费了很多资源，KV Cache 就是在这里使用的，我们在每次处理新的序列时，可以同时将之前计算的 key, value 一同缓存，并传入下一次计算，这样就节省了很多计算的时间，避免了冗余计算。

KV Cache 节省哪部分内容？

首先，我们要知道，Self-Attention 通过将输入序列变换成三个向量来操作：查询向量（Query），键向量（Key）和值向量（Value）。这些向量是通过对输入进行线性变换得到的。注意力机制基于$Q$ 向量和$K$向量之间的相似度来计算$V$向量的加权求和。然后，将这个加权求和的结果连同原始输入一起送入前馈神经网络，以产生最终输出。

这一过程允许模型专注于相关信息并捕捉长距离依赖关系。 那么回到问题，它节省了哪部分计算呢？它节省了对于键（Key）和值（Value）的重复计算，不需要对之前已经计算过的 Token 的$K$和 $V$重新进行计算。因为对于之前的 Token 可以复用上一轮计算的结果，避免了重复计算，只需要计算当前 Token 的$Q、K、V$。

MQA–多请求注意力

通过KV Cache虽然可以解决kv重复计算的问题，但当面对长上下文的时候，占用的显存是非常可观的。就拿llama3-8B模型来举例子，其模型序列长度 L=8192（即8K），Transformer层数 N=32，注意力头数 H=32，每个注意力头的维度 D=128，Batch按照1来计算，数据类型为BF16（2个字节），那么它所需要的缓存就为：
$$toke{n}_{kv}=2\times 1\times 32\times 8192\times 128\times 32\times 2=4294967296$$
换算成GB，则为4GB。为了解决这个问题，减少KV缓存一个最直观的方法。

那么MQA多注意力和GQA多注意力应运而生。那么这里首先开始从MQA讲起，多请求注意力（Multi-Query Attention，MQA）是多头注意力（Multi-Head Attention，MHA）的一种变体，由Google团队在2019年提出，其核心：旨在减少计算开销和显存占用，同时保持一定的模型性能。

在传统的MHA中，每个注意力头都有独立的查询（Query）、键（Key）和值（Value）矩阵，这使得每个头可以独立学习输入中的不同特性。而MQA的核心思想是让所有注意力头共享同一份Key和Value矩阵，仅保留Query的多头性质。这意味着在MQA中，Key和Value的计算是唯一的，而Query则根据不同的头进行独立转换。其优点是：1）KV Cache 显著减少，适合长序列推理；2）减少了计算和通信开销，推理速度提升 40-50%；缺点是：共享 K 和 V 可能导致模型捕捉上下文的能力下降，任务效果略有损失

原理介绍

MQA的核心思想是减少Key和Value矩阵的数量，从而降低计算和存储开销。在传统的MHA中，每个注意力头都有独立的Query（Q）、Key（K）和Value（V） 矩阵。

MQA的做法其实很简单。在MHA中，输入分别经过 $W_Q$、$W_K$、$W_V$ 的变换之后，都切成了n份（n=头数），维度也从 $d_{model}$ 降到了 $d_{head}$，分别进行attention计算再拼接。而MQA这里，在线性变换之后，只对 $Q$ 进行切分（和MHA一样），而 $K$、$V$ 则直接在线性变换的时候把维度降到了 $d_{head}$（而不是切分变小），然后这n个Query头分别和同一份 $K$、$V$ 进行attention计算，之后把结果拼接起来。其经典原理图如下所示：

简单来说，就是MHA中，每个注意力头的 $K$、$V$ 是不一样的，而MQA这里，每个注意力头的 $K$、$V$ 是一样的，值是共享的。而其他步骤都和MHA一样，具体计算原理图如下：

假设输入为hidden_states，其维度为(batch_size, sequence_length, hidden_size)，以下是MQA的详细计算过程：

---

1.线性变换：

Query：每个头的Query矩阵独立计算：
KaTeX parse error: Expected 'EOF', got '_' at position 33: …ot \text{hidden_̲states}
其中，$W^Q$ 是一个线性变换矩阵，维度为 $(hidde{n}_{s}ize,nu{m}_{h}eads\times hea{d}_{d}im)$。

Key：所有头共享同一个Key矩阵：
KaTeX parse error: Expected 'EOF', got '_' at position 33: …ot \text{hidden_̲states}
其中，$W^K$是一个线性变换矩阵，维度为$ (hidden_size, head_dim)$。

Value：所有头共享同一个Value矩阵：
$
V = W^V \cdot \text{hidden_states}
$
其中，$W^V$是一个线性变换矩阵，维度为$ (hidden_size, head_dim)$。

---

2.多头切分

Query：将Query矩阵按头进行切分：
$$Q_{\text{split}}=\text{reshape}(Q,(batch\_size,sequence\_length,num\_heads,head\_dim))$$
Key和Value：由于Key和Value是共享的，它们不需要按头切分，但需要扩展维度以匹配Query的维度：
$$K_{\text{split}}=K\cdot \text{expand}(1,nu{m}_{h}eads,1)$$
$$V_{\text{split}}=V\cdot \text{expand}(1,nu{m}_{h}eads,1)$$

---

3.注意力计算：

计算Query和Key之间的点积：
$$\text{scores}=\frac{Q_{\text{split}}\cdot K_{\text{split}}^T}{\sqrt{head\_dim}}$$
应用Softmax函数获取注意力权重：
$$\text{attention\_weights}=\text{softmax}(\text{scores})$$
使用注意力权重对Value进行加权求和：
$$\text{context}=\text{attention\_weights}\cdot V_{\text{split}}$$

---

4.多头合并：

将多头的输出合并为一个矩阵：
KaTeX parse error: Expected 'EOF', got '_' at position 20: … \text{context_̲merged} = \text…
通过一个线性变换矩阵 $W^O$\将合并后的矩阵映射到输出维度：
KaTeX parse error: Expected 'EOF', got '_' at position 46: …t \text{context_̲merged}

---

示例代码

import torch
import torch.nn as nn
import torch.nn.functional as F

class MultiQueryAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super(MultiQueryAttention, self).__init__()
        self.num_heads = num_heads
        self.d_model = d_model
        self.head_dim = d_model // num_heads

        assert (
            self.head_dim * num_heads == d_model
        ), "d_model must be divisible by num_heads"

        self.query_linear = nn.Linear(d_model, d_model)
        self.key_linear = nn.Linear(d_model, self.head_dim)
        self.value_linear = nn.Linear(d_model, self.head_dim)
        self.out_linear = nn.Linear(d_model, d_model)

    def forward(self, queries, keys, values, mask=None):
        batch_size = queries.size(0)

        # 线性变换
        Q = self.query_linear(queries)  # (batch_size, seq_len, d_model)
        K = self.key_linear(keys)       # (batch_size, seq_len, head_dim)
        V = self.value_linear(values)   # (batch_size, seq_len, head_dim)

        # 分割为多个头
        Q = Q.view(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)  # (batch_size, num_heads, seq_len, head_dim)
        K = K.unsqueeze(1).expand(-1, self.num_heads, -1, -1)                      # (batch_size, num_heads, seq_len, head_dim)
        V = V.unsqueeze(1).expand(-1, self.num_heads, -1, -1)                      # (batch_size, num_heads, seq_len, head_dim)

        # 计算注意力得分
        scores = torch.matmul(Q, K.transpose(-2, -1)) / torch.sqrt(torch.tensor(self.head_dim, dtype=torch.float32))
        if mask is not None:
            scores = scores.masked_fill(mask == 0, -1e9)
        attn = F.softmax(scores, dim=-1)
        # 计算注意力输出
        output = torch.matmul(attn, V)  # (batch_size, num_heads, seq_len, head_dim)
    
        output = output.transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)  # (batch_size, seq_len, d_model)

        return self.out_linear(output)


batch_size = 1
seq_len = 3
d_model = 4
num_heads = 2

# 随机生成输入张量
queries = torch.rand(batch_size, seq_len, d_model)
keys = torch.rand(batch_size, seq_len, d_model)
values = torch.rand(batch_size, seq_len, d_model)

# 初始化 MQA 模型
mqa = MultiQueryAttention(d_model, num_heads)

mask = torch.tril(torch.ones(seq_len, seq_len)).unsqueeze(0).unsqueeze(0)  # (1, 1, seq_len, seq_len)
print('mask:',mask)
# 前向传播
output = mqa(queries, keys, values,mask)

print("输出张量：")
print(output)

GQA–分组请求注意力

MHA为每个注意力头分配独立的查询、键和值矩阵，增强模型的表达能力，但也增加了计算和内存开销。MQA则让所有注意力头共享同一组键和值矩阵，显著降低了计算成本，但可能影响模型性能。GQA作为折衷方案，通过将查询向量分组，每组共享一组键和值矩阵，旨在在计算效率和模型性能之间取得平衡。在多头注意力（MHA）中，唯一键和值向量的数量等于注意力头的数量；在多查询注意力（MQA）中，唯一键和值向量的数量等于1。

在分组请求注意力（GQA）中，唯一键和值向量的数量等于超参数 G，即组的数量。例如，如果注意力头的数量为 4，且 G=2，那么将有两组唯一的键和值向量，每组将由两个注意力头使用：

原理介绍

GQA 的目标是还是减少自注意力计算的复杂度，同时保持 Transformer 的表达能力。它的核心改进点在于：让 多个 Query 共享少量的 Key 和 Value，减少计算开销，并通过通过 分组机制（Grouping Mechanism） 进行更高效的计算，如上图所示。除此之外，为了方便理解MHA、MQA、MGA这里再放一个最最经典的图。

在 GQA 中，Query 仍然是独立计算的，每个 Query 有自己的投影。但 Key 和 Value 是 共享的，它们被分组并被多个 Query 使用。GQA计算过程如下：

---

1、嵌入向量输入

假设输入序列为：
$$X\in {\mathbb{R}}^{n\times d}$$
其中：

• $n$ 是序列长度（tokens 数）
• $d$ 是隐藏层维度（embedding 维度）

在标准自注意力（Self-Attention）中，输入 $X$ 会被投影到 Query、Key、Value 三个子空间：
$$Q=X{W}_Q,K=X{W}_K,V=X{W}_V$$
其中 $W_Q,W_K,W_V$ 是可训练的投影矩阵。

---

2、Query多头计算

GQA 采用了分组键值（Grouped Key-Value, GKV），即：

• Query（查询）仍然是每个头独立计算的。
• Key 和 Value 共享，即 Key 和 Value 只计算少量的分组，然后多个 Query 共享这些值。

假设我们有 $h$ 个注意力头（Heads），Query 的计算方式如下：
$$Q_i=X{W}_Q^i,\text{for }i=1,2,...,h$$
其中：

• $W_Q^i$ 是第 $i$ 个头的 Query 投影矩阵。
• 计算出的 $Q_i$ 形状为 $(n,d_h)$，其中 $d_h=d/h$。

---

3、Key 和 Value 计算（共享分组）

在标准的 MHA（Multi-Head Attention）中，每个头都单独计算 $K$ 和 $V$。但在 GQA 中，我们将 Key 和 Value 分成 $g$ 组（Groups），其中 $g<h$，即：
$$K_j=X{W}_K^j,V_j=X{W}_V^j,\text{for }j=1,2,...,g$$
其中：

$W_K^j$ 和 $W_V^j$ 只计算 $g$ 组 Key 和 Value，而不是 $h$ 组。

计算出的 $K_j$ 和 $V_j$ 形状分别为 $(n,d_g)$，其中 $d_g=d/g$（即 Key 和 Value 维度比 MHA 更少）。

每个 $g$ 组的 Key 和 Value 将被多个 Query 共享。

这样，每个 Query 头不再独立拥有自己的 $K$ 和 $V$，而是共享一组 Key-Value，从而降低计算量。

---

4、计算注意力得分

注意力得分使用缩放点积注意力（Scaled Dot-Product Attention）：
$$A_i=\text{softmax}\left(\frac{Q_i{K}_j^T}{\sqrt{d_g}}\right)$$
其中：

• $Q_i$ 来自每个 Query 头。
• $K_j$ 来自共享的 Key 组。
• 由于 $K_j$ 被多个 $Q_i$ 共享，这减少了计算成本。
• 计算出的 $A_i$ 形状为 $(n,n)$。

---

5、计算加权 Value
$$Z_i=A_i{V}_j$$
其中：

• $A_i$ 是注意力得分（来自 Query 和 Key 计算）。
• $V_j$ 是共享的 Value 组。
• 计算出的 $Z_i$ 形状仍为 $(n,d_h)$。

---

6、 输出计算

所有注意力头计算的结果 $Z_i$ 会被拼接，然后经过最终的线性变换：
$$Z=[Z_1,Z_2,...,Z_h]W_O$$
其中：

• $W_O$ 是输出投影矩阵，最终得到形状为 $(n,d)$ 的输出。

---

示例代码

import torch
import torch.nn as nn

class GQA(nn.Module):
    def __init__(self, d_model, num_heads, num_groups):
        super(GQA, self).__init__()
        assert num_heads % num_groups == 0, "Heads should be evenly divisible by groups"
        self.num_heads = num_heads
        self.num_groups = num_groups
        self.d_model = d_model
        self.d_head = d_model // num_heads
        self.d_group = d_model // num_groups  # Key-Value 分组维度

        # Query 仍然是独立的
        self.W_q = nn.Linear(d_model, d_model, bias=False)
        # Key 和 Value 共享
        self.W_k = nn.Linear(d_model, d_model // num_groups * num_heads, bias=False)
        self.W_v = nn.Linear(d_model, d_model // num_groups * num_heads, bias=False)
        self.W_o = nn.Linear(d_model, d_model, bias=False)
    
    def forward(self, x):
        batch_size, seq_len, _ = x.shape

        # 计算 Query, Key, Value
        Q = self.W_q(x).view(batch_size, seq_len, self.num_heads, self.d_head)
        K = self.W_k(x).view(batch_size, seq_len, self.num_groups, self.d_group)
        V = self.W_v(x).view(batch_size, seq_len, self.num_groups, self.d_group)

        # 计算注意力分数
        attention_scores = torch.einsum("bqhd,bkgd->bhqk", Q, K) / (self.d_group ** 0.5)
        attention_weights = torch.softmax(attention_scores, dim=-1)

        # 计算注意力加权值
        Z = torch.einsum("bhqk,bkgd->bqhd", attention_weights, V)

        # 重新 reshape 并输出
        Z = Z.reshape(batch_size, seq_len, self.d_model)
        return self.W_o(Z)

MLA–多潜头注意力

原理介绍

MLA（Multi-Head Local Attention）的基本思想是将注意力输入 $h_t$ 压缩成一个低维的潜在向量，维度为 $d_c$，其中 $d_c$ 远小于原始的维度（$h_n\cdot d_h$）。在需要计算注意力时，可以将这个潜在向量映射回高维空间，从而恢复键（keys）和值（values）。因此，只需要存储潜在向量，从而显著减少了内存的占用。

先看以下DS得MLA的流程图：

再看一下公式表示：

很懵对不对？仔细看解释来了。

公式（37-40）主要是为了计算Q（即Attention中的Q矩阵）。

公式（37）通过$W^{DQ}$矩阵对$h_t$实现降维；

公式（38）通过$W^{UQ}$矩阵来实现对$c_t^Q$的升维，这样$h_t$一降一升，就大幅降低了$h_t$本身的权重矩阵参数。

公式（39）通过$W^{QR}$矩阵对$c_t^Q$进行映射计算，这里在DeepSeek论文中，相当于对$c_t^Q$又做了一次降维，然后对其做旋转位置编码。（这里为什么要单独做RoPE位置编码呢？可以看后面，为什么需要解耦的RoPE？）

公式（40）$h_t$一降一升后的$q_t^C$，再拼接上旋转位置编码$q_t^R$。这样相当于得到了MHA中的Q。

公式（40-45）主要是为了计算K、V（即Attention中的Q矩阵）。

公式（41）通过$W^{DKV}$矩阵对$h_t$实现降维；

公式（42）通过$W^{UKV}$矩阵对$h_t$实现升维，得到$k_t^C$和前面计算Q一样，通过$h_t$一降一升，就大幅降低了$h_t$本身的权重矩阵参数。

公式（43）通过$W^{KR}$矩阵对$h_t$进行映射计算，然后对其做RoPE位置编码。（这里和计算Q的旋转位置编码不一样）

公式（44）将$k_t^C$的每个头的计算结果分别与RoPE位置编码后的$k_t^R$进行拼接得到k，这样相当于得到了MHA中的K。

公式（45）主要是计算$V$矩阵。

公式（46-47）分别计算每个头的注意力，然后拼接到一块，接着利用$W^O$做个映射，完成Attention计算。

在此过程中，只有上述公式中，带框的蓝色变量需要被缓存，其它的都可以利用“矩阵吸收”，重新恢复过来。

细节介绍

为什么需要解耦的RoPE？

RoPE是训练生成模型以处理长序列的常用选择，简单应用案例如下。如果直接应用上述MLA策略，这将与RoPE不兼容，为什么呢？

为了更清楚地理解这一点，考虑当我们使用公式${\mathbf{q}}_{t,i}^T{\mathbf{k}}_{j,i}^C$计算注意力时会发生什么：将$q$得转置与$k$相乘时，矩阵$W^{UQ}$和$W^{UK}$将出现在中间，它们的组合等价于一个从$d_c$到$d$的单一映射维度。

$q_{t,i}^T\times k_{j,i}=(W_{(i)}^{UQ}{c}_t^Q{)}^T\times W_{(i)}^{UK}{c}_j^{KV}=(c_t^Q{)}^T\times (W_{(i)}^{UQ}{)}^T{W}_{(i)}^{UK}\times c_j^{KV}(1)$

不加RoPE，我们可以提前计算好 $(W_{(i)}^{UQ}{)}^T{W}_{(i)}^{UK}$，也就上面说的 $W^{UK}$ 吸收到 $W^{UQ}$ 中，这样在做 $q$ 的变换的时候，也就同时计算了 $W^{UK}$ 矩阵的乘法。这样的好处是，我们只需要缓存 $c_j^{KV}$，而不是缓存 $W_{(i)}^{UK}\times c_j^{KV}$ 的结果。这就是MLA的压缩KV Cache的核心原理。

加上RoPE后，为什么不兼容？，计算 $q,k$ 乘积，会在 $(W_{(i)}^{UQ}{)}^T$ 和 $W_{(i)}^{UK}$ 之间，增加一个融合了相对位置的变量 ${\mathcal{R}}_{t-j}$，如公式所示：
$$q_{t,i}^T\times k_{j,i}=({\mathcal{R}}_t{W}_{(i)}^{UQ}{c}_t^Q{)}^T\times {\mathcal{R}}_j{W}_{(i)}^{UK}{c}_j^{KV}=(c_t^Q{)}^T\times (W_{(i)}^{UQ}{)}^T{\mathcal{R}}_t^T{\mathcal{R}}_j{W}_{(i)}^{UK}\times c_j^{KV}$$

$$=(c_t^Q{)}^T\times (W_{(i)}^{UQ}{)}^T{\mathcal{R}}_{t-j}{W}_{(i)}^{UK}\times c_j^{KV}(2)$$

中间这个分量 $(W_{(i)}^{UQ}{)}^T{\mathcal{R}}_{t-j}{W}_{(i)}^{UK}$ 是随这相对位置变化而变化的，并不是个固定的矩阵，因此并不能提前计算好。所以论文中说RoPE与低秩变换不兼容。（这里对旋转位置编码不熟悉的小伙伴可以重新了解一下旋转位置编码）

怎么解决RoPE不兼容问题呢？—>通过增加一个很小 $q,k$ 分量，引入RoPE

为了引入位置编码，作者在一个很小维度下，用MQA方式计算了 $q,k$，也就是在每层网络中，所有Head只计算一个 $k$（如论文中公式43所示）。引入位置编码的向量维度取的比较小为：$d_h/2=128/2=64$。

所以最终 $q,k$ 向量通过两部分拼接而成，计算权重时，由前后两部分分别相乘再相加得到，如下公式所示：

$$q_{t,i}^T\times k_{j,i}=[q_{t,i}^C;q_{t,i}^R{]}^T\times [k_{j,i}^C;k_t^R]=q_{t,i}^C{k}_{j,i}^C+q_{t,i}^R{k}_t^R(3)$$

前一项 $q_{t,i}^C{k}_{j,i}^C$ 按公式（1）计算，通过矩阵吸收处理，全Head只缓存一个 $c_t^{KV}$，后一项 $q_{t,i}^R{k}_t^R$ 按正常MQA的方式计算，全Head只缓存了一个共享 $k$。

通过类似的计算方式，可以处理将 $v$ 的变换矩阵 $W^{UV}$ 吸收到最终的结果变换矩阵 $W^O$ 中，这样也不用实际计算和缓存 $v$ 的值。而是只缓存跟 $k$ 一样的 $c_t^{KV}$ 即可。

示例代码

## DeepSeek MLA源码
class MLA(nn.Module):
    """
    Multi-Headed Attention Layer (MLA).

    Attributes:
        dim (int): Dimensionality of the input features.
        n_heads (int): Number of attention heads.
        n_local_heads (int): Number of local attention heads for distributed systems.
        q_lora_rank (int): Rank for low-rank query projection.
        kv_lora_rank (int): Rank for low-rank key/value projection.
        qk_nope_head_dim (int): Dimensionality of non-positional query/key projections.
        qk_rope_head_dim (int): Dimensionality of rotary-positional query/key projections.
        qk_head_dim (int): Total dimensionality of query/key projections.
        v_head_dim (int): Dimensionality of value projections.
        softmax_scale (float): Scaling factor for softmax in attention computation.
    """
    def __init__(self, args: ModelArgs):
        super().__init__()
        self.dim = args.dim  # 输入特征的维度d
        self.n_heads = args.n_heads # 128
        self.n_local_heads = args.n_heads // world_size  # word_size = 1  进程数
        self.q_lora_rank = args.q_lora_rank  # 低秩查询投影的秩   0表示不使用低秩 1536
        self.kv_lora_rank = args.kv_lora_rank # 低秩键/值投影的秩 512
        self.qk_nope_head_dim = args.qk_nope_head_dim # 128
        self.qk_rope_head_dim = args.qk_rope_head_dim # 64
        self.qk_head_dim = args.qk_nope_head_dim + args.qk_rope_head_dim  # 128+64
        self.v_head_dim = args.v_head_dim # 128

        if self.q_lora_rank == 0:
            self.wq = ColumnParallelLinear(self.dim, self.n_heads * self.qk_head_dim)
        else:
            self.wq_a = Linear(self.dim, self.q_lora_rank) # q_lora_rank = 1536   7168*1536
            self.q_norm = RMSNorm(self.q_lora_rank) # 1536
            self.wq_b = ColumnParallelLinear(self.q_lora_rank, self.n_heads * self.qk_head_dim) # 1536 * 128*(128+64)
        self.wkv_a = Linear(self.dim, self.kv_lora_rank + self.qk_rope_head_dim) # 7168*(512+64)
        self.kv_norm = RMSNorm(self.kv_lora_rank)  # 512
        self.wkv_b = ColumnParallelLinear(self.kv_lora_rank, self.n_heads * (self.qk_nope_head_dim + self.v_head_dim)) # 512 * 128*(128+128)
        self.wo = RowParallelLinear(self.n_heads * self.v_head_dim, self.dim)  # 128*128 * 7168
        self.softmax_scale = self.qk_head_dim ** -0.5
        if args.max_seq_len > args.original_seq_len:              
            mscale = 0.1 * args.mscale * math.log(args.rope_factor) + 1.0
            self.softmax_scale = self.softmax_scale * mscale * mscale

        if attn_impl == "naive":
            self.register_buffer("k_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.qk_head_dim), persistent=False)
            self.register_buffer("v_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.n_local_heads, self.v_head_dim), persistent=False)
        else:
            self.register_buffer("kv_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.kv_lora_rank), persistent=False)
            self.register_buffer("pe_cache", torch.zeros(args.max_batch_size, args.max_seq_len, self.qk_rope_head_dim), persistent=False)

    def forward(self, x: torch.Tensor, start_pos: int, freqs_cis: torch.Tensor, mask: Optional[torch.Tensor]):
        """
        Forward pass for the Multi-Headed Attention Layer (MLA).

        Args:
            x (torch.Tensor): Input tensor of shape (batch_size, seq_len, dim).
            start_pos (int): Starting position in the sequence for caching.
            freqs_cis (torch.Tensor): Precomputed complex exponential values for rotary embeddings.
            mask (Optional[torch.Tensor]): Mask tensor to exclude certain positions from attention.

        Returns:
            torch.Tensor: Output tensor with the same shape as the input.
        """
        bsz, seqlen, _ = x.size()  # batch_size, seq_len, dim   1，2，7168
        end_pos = start_pos + seqlen
        if self.q_lora_rank == 0:
            q = self.wq(x)
        else:
            q = self.wq_b(self.q_norm(self.wq_a(x)))  #  1，2，7168 -->  1，2，1536  --> 1，2，128*(128+64)  先降维，再升维
        q = q.view(bsz, seqlen, self.n_local_heads, self.qk_head_dim)  # 1，2，128，128+64
        q_nope, q_pe = torch.split(q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1) # 对最后一个维度进行切分 1，2，128，128 && 1，2，128，64
        q_pe = apply_rotary_emb(q_pe, freqs_cis)
        kv = self.wkv_a(x)  # 1，2，7168 --> 1，2，512+64  （） # 直接降维
        kv, k_pe = torch.split(kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1)  # 1，2，512 && 1，2，64
        k_pe = apply_rotary_emb(k_pe.unsqueeze(2), freqs_cis) # 1，2，1，64
        if attn_impl == "naive":
            q = torch.cat([q_nope, q_pe], dim=-1) # 1，2，128，128+64
            kv = self.wkv_b(self.kv_norm(kv)) # 1，2，512 --> 1，2，128*(128+128)  对kv进行生维
            kv = kv.view(bsz, seqlen, self.n_local_heads, self.qk_nope_head_dim + self.v_head_dim)  # 1，2，128，128+128（516）
            k_nope, v = torch.split(kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1) # 1，2，128，128 && 1，2，128，128
            k = torch.cat([k_nope, k_pe.expand(-1, -1, self.n_local_heads, -1)], dim=-1) # 1，2，128，128 && 1，2，1，64  --> 1，2，128，128+64
            self.k_cache[:bsz, start_pos:end_pos] = k
            self.v_cache[:bsz, start_pos:end_pos] = v
            scores = torch.einsum("bshd,bthd->bsht", q, self.k_cache[:bsz, :end_pos]) * self.softmax_scale  # 1，2，128，128  * 1，2，128，128+64
        else:
            wkv_b = self.wkv_b.weight if self.wkv_b.scale is None else weight_dequant(self.wkv_b.weight, self.wkv_b.scale, block_size) # 512 * 128*(128+128)
            wkv_b = wkv_b.view(self.n_local_heads, -1, self.kv_lora_rank) # 128, 128+128, 512
            q_nope = torch.einsum("bshd,hdc->bshc", q_nope, wkv_b[:, :self.qk_nope_head_dim]) # 1，2，128，128
            self.kv_cache[:bsz, start_pos:end_pos] = self.kv_norm(kv) # 1，2，512 --> 1，2，512
            self.pe_cache[:bsz, start_pos:end_pos] = k_pe.squeeze(2) # 1，2，1，64 --> 1，2，64
            scores = (torch.einsum("bshc,btc->bsht", q_nope, self.kv_cache[:bsz, :end_pos]) +
                      torch.einsum("bshr,btr->bsht", q_pe, self.pe_cache[:bsz, :end_pos])) * self.softmax_scale # 1，2，128，128  * 1，2，128，128+64
        if mask is not None:
            scores += mask.unsqueeze(1)
        scores = scores.softmax(dim=-1, dtype=torch.float32).type_as(x)
        if attn_impl == "naive":
            x = torch.einsum("bsht,bthd->bshd", scores, self.v_cache[:bsz, :end_pos]) # 1，2，128，128
        else:
            x = torch.einsum("bsht,btc->bshc", scores, self.kv_cache[:bsz, :end_pos])
            x = torch.einsum("bshc,hdc->bshd", x, wkv_b[:, -self.v_head_dim:])
        x = self.wo(x.flatten(2)) # 1，2，128，128 --> 1，2，7168
        return x

MHA、MQA、GQA、MLA实验结果对比

下表比较了 MHA、GQA、MQA 和 MLA 之间每个 token 所需的 KV 缓存元素数量以及建模容量，表明 MLA 确实可以在内存效率和建模容量之间取得更好的平衡。

更具体地说，下表展示了 MHA、GQA 和 MQA 在 7B 模型上的表现，其中 MHA 明显优于 MQA 和 GQA。

对 MHA 和 MLA 进行了分析，结果总结在下表中，其中 MLA 整体上取得了更好的效果。

文中公式表达或有错误，欢迎批评指正！

>>>>专注大模型/AIGC、学术前沿的知识分享！

参考文献

https://www.zhihu.com/question/68482809/answer/264632289

http://www.sniper97.cn/index.php/note/deep-learning/note-deep-learning/4002/

https://www.linsight.cn/3dc22f96.html

https://blog.youkuaiyun.com/qq_35229591/article/details/142334265