leetcode69.x的平方根(java)：牛顿迭代法

法一：牛顿迭代法

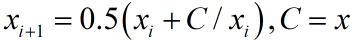
具体代码

class Solution {
    public int mySqrt(int x) {
        if(x == 0){
            return 0;
        }
        double C = x, x0 = x;
        while(true){
            double xi = 0.5 * (x0 + C/x0);
            if(Math.abs(xi - x0) < 1e-7){
                break;
            }
            x0 = xi;
        }
        return (int)x0;
    }
}

法二：二分查找法

class Solution {
    public int mySqrt(int x) {
        if(x == 0){
            return 0;
        }
       int l = 0, r = x, ans = -1;
       while(l <= r){
           int mid = l + ((r - l)>>1);
           if((long)mid * mid <= x){
               ans = mid;
               l = mid + 1;
           }else{
               r = mid - 1;
           }
       }
       return ans;
    }
}

法三：袖珍计算器算法

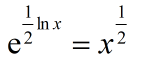
具体代码

class Solution {
    public int mySqrt(int x) {
        if(x == 0){
            return 0;
        }
        int ans = (int)Math.exp(0.5 * Math.log(x));
        return (long)(ans+1)*(ans+1) <= x?ans+1:ans;
    }
}

注意：ans*ans可能会越界，所以要使用long

参考资料
leetcode官方题解