大脑中的神经网络
神经元是构成神经网络的基本单位,每个神经元包含一个神经核/处理单元(Nucleus/processing unit),多个树突/输入(Dendrite/input),一个轴突/输出(output/Axon).神经网络是大量的这样的神经元相互连接并通过电波信号进行交流的一个网络。神经元示意图如下图:
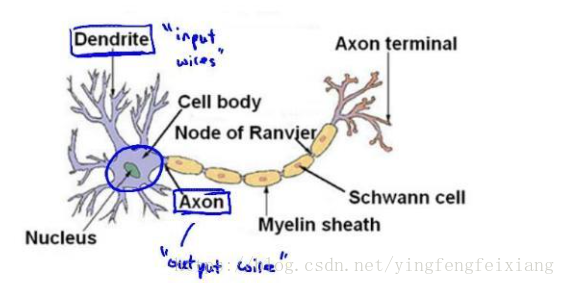
神经元模型
神经元模型是一个一个的学习模型,逻辑回归作为神经元的示例。
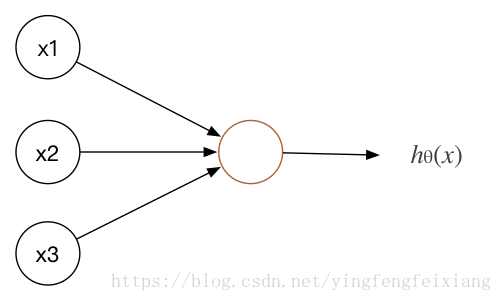
图中hθ(x)=11+e−θTxhθ(x)=11+e−θTx.
然后可以设计出类似于神经元的神经网络,如下图:
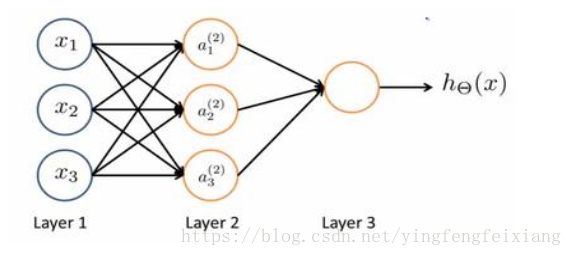
其中x1,x2,x3x1,x2,x3是输入单元(input units),将原始数据输入给它们。a1,a2,a3a1,a2,a3是中间单元,它们负责将数据进行处理,然后呈递给下一层。最后是输出单元,计算hθ(x)hθ(x).
实际应用的网络模型:
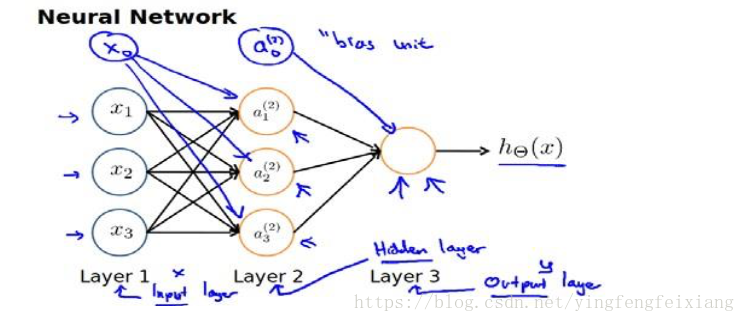
上图展示的是一个3层的神经网络,第一层为输入层(Input Layer)、中间层为隐藏层(Hidden Layer)、第三层为输出层(Output Layer).在神经网络模型中,除了输出层,每一层都增加了一个偏差单位(bais unit).
a(j)iai(j)代表第jj层的第个激活单元。θ(j)θ(j)代表从第jj层映射到第层是的权重矩阵。例如θ(1)θ(1)代表从第一层映射到第二层的权重的矩阵。
上图所示模型,激活单元和输出分别表达为:
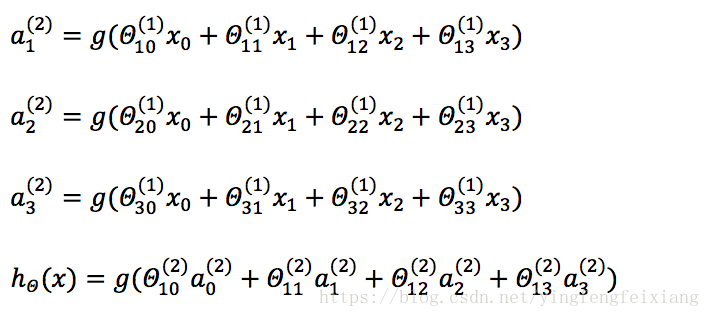
三层神经网络可以理解为:
假如每一层的计算函数为Sigmoid函数,输入层xixi和θ1iθi1通过隐藏层Sigmoid函数hθ(x)=11+e−θTxhθ(x)=11+e−θTx计算得到a(j)iai(j);而a(j)iai(j)和θ2iθi2作为输出层Sigmoid函数的输入,通过函数hθ(x)=11+e−θTa(j)ihθ(x)=11+e−θTai(j)得到最后的输出。
可以把a0,a1,a2,a3a0,a1,a2,a3看成更高级的特征值,x0,x1,x2,x3x0,x1,x2,x3的进化体,并且它们由xx决定的,由于是梯度下降,所以是变化的,并且越来越厉害,也就是说这些学习到的更高级的特征要比xx更能较好的预测新数据。所以神经网络比逻辑回归和线性回归更具有优势。
























 12万+
12万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








