搜广推校招面经三十五

最新推荐文章于 2025-08-20 19:27:37 发布

Y1nhl

最新推荐文章于 2025-08-20 19:27:37 发布

阅读量889

点赞数 20

CC 4.0 BY-SA版权

分类专栏：搜广推面经文章标签：数据挖掘人工智能机器学习推荐算法 python 搜索算法 pytorch

本文链接：https://blog.youkuaiyun.com/yin2567588841/article/details/145993689

搜广推面经专栏收录该内容

108 篇文章

订阅专栏

Construct 推荐算法

一、Gini指标的概念

Gini 指标是一种用于衡量数据集纯度或不纯度的指标，广泛应用于决策树算法（如 CART 算法）中，用来选择最佳的特征分裂点。以下是 Gini 指标的详细概念和计算方法：

1.1. Gini指标在分类任务中的应用

1.1.1. Gini 指标的基本概念

定义: Gini 指标表示一个随机选中的样本被错误分类的概率。
取值范围: Gini 值介于 0 和 1 之间：
- 当 Gini = 0 时，表示数据集完全纯净（所有样本属于同一类别）。
- 当 Gini 接近 1 时，表示数据集非常不纯（样本类别分布均匀）。

1.1.2. Gini 指标的公式

对于一个包含 $k$ 个类别的数据集 $D$ ，其 Gini 指标可以定义为：
$\sum_{i=1}^{k} p_i^2$
其中：

$p_i$ 表示第 $i$ 类样本在数据集中所占的比例。
$∑i=1kpi2\sum_{i=1}^{k} p_i^2$ 是所有类别概率平方的总和，表示数据集的纯度。

1.1.3. Gini 指标的性质

纯度越高，Gini 越小: 当数据集中某一类别的比例接近 1（即几乎全是该类别），则 Gini 值接近 0。
类别分布越均匀，Gini 越大: 当数据集中各类别比例相等时，Gini 值达到最大。

1.1.4. Gini 指标与熵的区别

特性	Gini 指标	熵 (Entropy)
计算复杂度	更简单，只需平方运算	较复杂，涉及对数运算
数据敏感性	对类别分布变化的敏感性较低	对类别分布变化的敏感性较高
决策树算法中的应用	CART 算法	ID3 和 C4.5 算法

1.2. Gini 指标在回归任务中的应用

在回归任务中，Gini 指标可以通过衡量预测值与真实值之间的分布差异来评估模型性能。具体来说，Gini 指标可以基于洛伦兹曲线（Lorenz Curve）进行计算，并通过比较预测值和真实值的分布面积比来量化模型的表现。

1.2.1. 回归任务中的 Gini 指标定义

在回归问题中，Gini 指标的核心思想是通过以下步骤计算：

排序: 将预测值按大小排序。
构建洛伦兹曲线: 根据排序后的预测值和真实值的比例分布，绘制洛伦兹曲线。
计算面积比: 计算洛伦兹曲线与完美预测曲线之间的面积比。

1.2.2. 具体计算步骤

(1) 排序

将所有样本的真实值 $y_i$ 和预测值 $y^i\hat{y}_i$ 按预测值 $y^i\hat{y}_i$ 的大小排序。
排序后，形成一个有序的样本列表。

(2) 构建洛伦兹曲线

洛伦兹曲线描述了累积预测值与累积真实值之间的关系。
定义：
- 累积比例：按照排序后的样本，计算前 $k$ 个样本的预测值和真实值占总和的比例。
- 横轴：累积样本比例（从 0 到 1）。
- 纵轴：累积真实值比例（从 0 到 1）。

(3) 计算 Gini 系数

Gini 系数定义为洛伦兹曲线与完美预测曲线之间的面积比。
公式：
$\frac{A}{A + B}$
其中：
- $A$ 是洛伦兹曲线与对角线（完美预测曲线）之间的面积。
- $B$ 是洛伦兹曲线与横轴之间的面积。
当 $G ini = 1$ 时，表示预测值与真实值完全不相关。
当 $G ini = 0$ 时，表示预测值与真实值完全一致。

1.2.3. 回归任务中 Gini 指标的直观理解

在回归任务中，Gini 指标衡量的是预测值对真实值分布的拟合程度。
如果预测值能够很好地捕捉真实值的分布趋势，则 Gini 指标会接近 0。
如果预测值与真实值分布完全无关，则 Gini 指标会接近 1。

1.2.4 总结

在回归任务中，Gini 指标通过洛伦兹曲线和面积比来衡量预测值与真实值之间的分布差异。它提供了一种直观的方式来评估模型的预测能力，尤其是在需要关注分布拟合的任务中非常有用。然而，需要注意的是，Gini 指标更适合用于相对排序的评估，而非绝对误差的度量。

二、长尾分布、零膨胀分布与多峰分布的介绍及解决方法

在数据分析和建模中，经常会遇到长尾分布、零膨胀分布以及多峰分布等特殊的数据分布形态。这些分布可能对模型性能产生显著影响，因此需要采取适当的策略进行处理。

2.1. 长尾分布

长尾分布是一种概率分布，其中大部分数据集中在某一区域，而少数极端值分布在尾部。

2.1.1. 特点

尾部数据稀疏，但可能包含重要信息。模型容易受到头部数据的影响，而忽略尾部数据。

2.1.2. 解决方法

数据变换：
- 使用对数变换（log(x + 1)）或幂变换（如 Box-Cox 变换）将长尾分布转换为近似正态分布。
采样技术：
- 对尾部数据进行过采样（Oversampling），增强模型对尾部数据的学习能力。
分层建模：
- 针对头部和尾部分别构建不同的模型，例如使用混合模型（Mixture Model）。
特征工程：
- 提取尾部数据的特定特征，增强模型对稀疏数据的表达能力。
- 变换目标（比如房价，大部分价格都是百万级别，尾巴肯定有千万、上亿的，可以通过房价/面积得到每平方价格，用每平方价格当作标签计数）

2.2. 零膨胀分布

零膨胀分布是指数据中存在大量零值，且零值的比例远高于其他值。

2.2.1. 特点

数据分布呈现双峰或多峰，其中一个峰位于零点。零值具有特殊的业务含义（如未发生事件）。

2.2.2. 解决方法

零膨胀模型：
- 使用零膨胀泊松回归（Zero-Inflated Poisson, ZIP）或零膨胀负二项回归（Zero-Inflated Negative Binomial, ZINB）来建模。
数据分割：
- 将零值和非零值分开处理，分别建模。

2.3. 多峰分布

多峰分布是指数据的概率密度函数存在多个峰值，表明数据可能来自多个不同的子群体。

2.3.1. 特点

数据难以用单一模型拟合。不同峰值可能对应不同的业务逻辑或物理过程。

2.3.2. 解决方法

混合模型：
- 使用高斯混合模型（Gaussian Mixture Model, GMM）或其他混合模型对数据进行聚类，识别不同子群体。
分组建模：
- 根据业务规则或聚类结果将数据划分为多个子集，分别建模。
特征工程：
- 提取能够区分不同峰值的特征，增强模型的分辨能力。
非参数方法：
- 使用核密度估计（Kernel Density Estimation, KDE）等非参数方法分析数据分布。

三、分类任务中，针对不平衡数据集怎么处理？

开始吟唱吧！！

四、ItemCF 和 UserCF 的区别

ItemCF（基于物品的协同过滤）和 UserCF（基于用户的协同过滤）是推荐系统中两种经典的协同过滤算法。它们的核心思想都是通过计算相似性来进行推荐（通常使用余弦相似度、皮尔逊相关系数等方法），但在具体实现和应用场景上存在显著差异。

4.1. UserCF

基于用户相似性的推荐方法。

核心思想: 找到与目标用户兴趣相似的其他用户，然后将这些相似用户喜欢但目标用户未接触过的物品推荐给目标用户。
更适合用户行为数据丰富且用户群体较小的场景。

4.2. ItemCF

基于物品相似性的推荐方法。

核心思想: 找到与目标用户已交互过的物品相似的其他物品，然后将这些相似物品推荐给目标用户。
更适合物品数量较少或用户行为数据稀疏的场景。

五、739. 每日温度（力扣hot100_栈_中等）

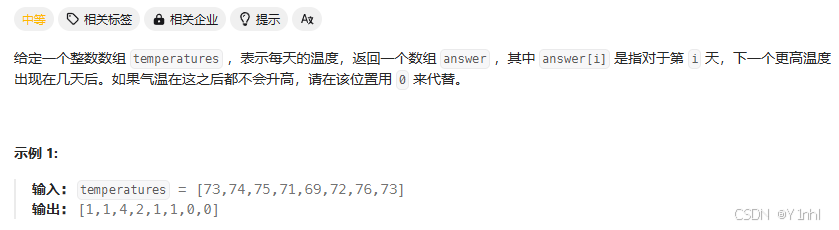
在这里插入图片描述

思路：
栈中记录还没算出下一个更大元素的那些数的下标。相当于栈是一个 todolist，在循环的过程中，现在还不知道答案是多少，在后面的循环中会算出答案。
思路：

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        n = len(temperatures)
        ans = [0] * n
        st = []  # todolist
        for i, t in enumerate(temperatures):
            while st and t > temperatures[st[-1]]:
                j = st.pop()
                ans[j] = i - j
            st.append(i)
        return ans