搜广推校招面经五十九

百度推荐算法

一、召回项目的指标，MRR 和 Hit Rate 的对比

在评估召回效果时，MRR（Mean Reciprocal Rank） 和 Hit Rate（命中率） 是常见的指标，但它们的衡量方式和适用场景有所不同。

1.1. MRR（Mean Reciprocal Rank，平均倒数排名）

MRR 衡量的是第一个正确命中的位置的平均倒数，主要用于评估推荐列表的排序质量。

计算公式

$$MRR=\frac{1}{N}\sum _{i=1}^N\frac{1}{ran{k}_i}$$
其中：

• $N$ 是测试样本总数
• $ran{k}_i$ 是第 $i$ 个测试样本在推荐列表中第一个正确命中项的排名
• 如果在推荐列表中没有正确命中，默认该样本的贡献为 0

优缺点

✅ 适用于关注前列推荐质量的场景，如搜索引擎、问答系统等。
✅ 能够反映相关项是否排在前面，比单纯的命中率更关注排序效果。
❌ 对长列表的影响较小，后面正确的项不会对指标产生影响。

示例

假设有 3 个查询，它们的推荐列表如下（✅ 代表真实目标项命中位置）：

查询	推荐列表	命中排名	贡献值 $\frac{1}{rank}$
Q1	A, B, ✅ C, D	3	1/3
Q2	✅ X, Y, Z, W	1	1/1
Q3	L, M, N, O, ✅ P	5	1/5

计算：
$$MRR=\frac{1}{3}\left(\frac{1}{3}+1+\frac{1}{5}\right)=\frac{1}{3}\times \frac{23}{15}\approx 0.51$$

1.2. Hit Rate（命中率，HR@K）

Hit Rate 关注的是推荐列表中是否命中目标项，不考虑排名。它通常用来衡量推荐系统的覆盖能力。

计算公式

$$HR@K=\frac{\text{命中次数}}{N}$$
其中：

• 命中：如果目标项在推荐列表前 $K$ 项中出现，记为 1，否则记为 0
• N：测试样本总数

优缺点

✅ 适用于推荐系统的召回阶段，主要衡量是否命中，不关注排名。
✅ 更容易提升，可以通过增加候选集或扩大推荐列表长度提高 HR@K。
❌ 不关注排名，无法衡量模型的排序质量。

示例

如果推荐列表长度为 $K=3$，假设有 5 个查询，它们的推荐列表如下：

查询	推荐列表	目标项是否命中前 3	贡献值
Q1	✅ A, B, C, D	✅	1
Q2	X, ✅ Y, Z, W	✅	1
Q3	L, M, N, O	❌	0
Q4	✅ P, Q, R, S	✅	1
Q5	U, V, ✅ W, X	✅	1

计算：
$$HR@3=\frac{1+1+0+1+1}{5}=\frac{4}{5}=0.8$$

1.3. MRR vs. Hit Rate 对比

指标	关注点	是否考虑排名	适用场景
MRR	目标项出现的排名位置	✅ 是	排序很重要的任务（如搜索、问答）
Hit Rate	是否命中目标项	❌ 否	召回阶段、曝光率、覆盖率衡量

适用场景对比

• MRR 更关注前列排序的质量，适用于需要把相关项排在前面的任务，例如搜索引擎、问答系统、个性化推荐等。
• Hit Rate 适用于召回阶段，更关注召回的覆盖范围，比如电商推荐、信息流推荐等，HR 高但 MRR 低可能表示推荐命中但排序不好。

二、LTV预估项目的Gini指标如何计算？含义是什么？

见【搜广推校招面经三十五】
参考：https://www.kilians.net/post/gini-coefficient-intuitive-explanation/

2.1. 什么是 Gini 指标？

Gini 指标（或 Gini 系数）是衡量模型预测性能的一种常见指标，尤其适用于 不平衡数据集，广泛应用于信用评分、保险风险预测等领域。它与 AUC（Area Under the Curve）密切相关，但更强调对排序的评价。

主要形式：

• Normalized Gini: 用于衡量模型排序的质量。
• Gini Impurity（基尼不纯度）: 用于决策树算法中衡量某特征的纯度。

2.2. Gini 指标的两种常见形式

2.2.1. Normalized Gini Coefficient（归一化 Gini 系数）

• 用于衡量模型预测结果的排序质量，广泛应用于信用评分和保险定价预测中。
• 与 AUC 相似，但侧重于样本排序的能力，能够更加准确地反映模型在不平衡数据集
• 公式：
  $$\text{Gini}=\frac{{\sum }_{i=1}^n{C}_i}{\text{TotalLosses}}-\frac{n+1}{2}$$

其中：

• $C_i$ 是按预测值排序后的累计损失，
• TotalLosses 是所有实际标签的总和，
• $n$ 是样本的数量。

归一化 Gini 系数

归一化 Gini 系数的计算为：
$$\text{Normalized Gini}=\frac{\text{Gini}(actual,pred)}{\text{Gini}(actual,actual)}$$

其中：

• Gini(actual, actual) 是与完全正确排序相比的 Gini 值（即完美模型的 Gini 值）。

2.2.2. Python 代码实现 Gini 指标计算

import numpy as np
def gini(actual, pred, cmpcol=0, sortcol=1):
    """
    计算 Gini 指标
    :param actual: 实际标签
    :param pred: 预测值
    :param cmpcol: 排序依据的列（实际标签列）
    :param sortcol: 排序依据的列（预测值列）
    :return: Gini 系数
    """
    assert (len(actual) == len(pred))
    # 将实际标签、预测值和索引组合成数组
    all = np.asarray(np.c_[actual, pred, np.arange(len(actual))], dtype=np.float)
    # 按照预测值降序排列，若预测值相同则按索引升序排列
    all = all[np.lexsort((all[:, 2], -1 * all[:, 1]))]
    totalLosses = all[:, 0].sum()  # 计算总损失
    giniSum = all[:, 0].cumsum().sum() / totalLosses  # 累积损失

    # 调整 Gini 值，使其满足标准
    giniSum -= (len(actual) + 1) / 2.
    return giniSum / len(actual)

def gini_normalized(actual, pred):
    """
    计算归一化 Gini 指标
    :param actual: 实际标签
    :param pred: 预测值
    :return: 归一化 Gini 系数
    """
    return gini(actual, pred) / gini(actual, actual)

三、23. 合并 K 个升序链表（力扣hot100_困难）

这道题有个简单版，合并两个有序链表

3.1. 21. 合并两个有序链表（力扣hot100_简单）

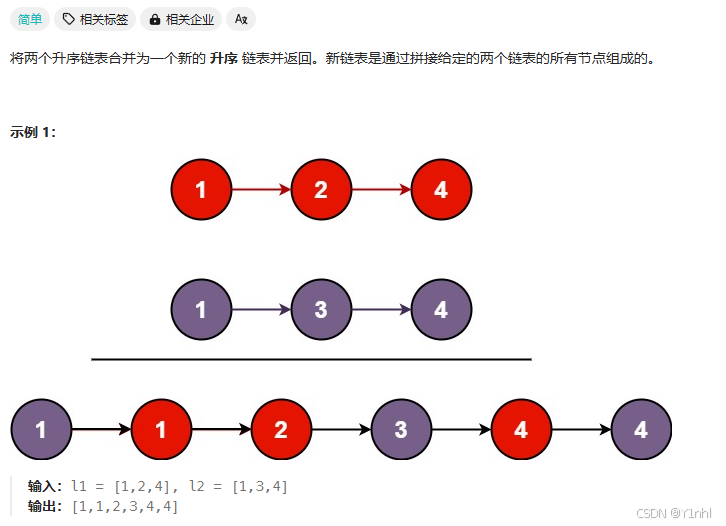
• 代码：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        dummy = ListNode()
        cur = dummy
        while list1 and list2:
            if list1.val <= list2.val:
                cur.next = list1
                cur = cur.next
                list1 = list1.next
            else:
                cur.next = list2
                cur = cur.next
                list2 = list2.next
        if list1:
            cur.next = list1
        else:
            cur.next = list2
        return dummy.next

3.2. 思路1：分治

这道题可以暴力求解，利用上述代码，先两两排序，再排第三列，… 一直到第K列完
如果不暴力的话？可以如何做？分治！k个list分成两份，先合并前一半的链表，再合并后一半的链表，然后把这两个链表合并成最终的链表。如何合并前一半的链表呢？我们可以继续一分为二。如此分下去直到只有一个链表，此时无需合并。

class Solution:
    # 21. 合并两个有序链表
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]):
    	...
    	
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        m = len(lists)
        if m == 0: return None                   # 注意输入的 lists 可能是空的
        if m == 1: return lists[0]               # 无需合并，直接返回
        left = self.mergeKLists(lists[:m // 2])  # 合并左半部分
        right = self.mergeKLists(lists[m // 2:])  # 合并右半部分
        return self.mergeTwoLists(left, right)    # 最后把左半和右半合并