本文深入解析PLA(感知器学习算法)的工作原理，通过不断修正权重向量来实现对数据的完美分类。从几何角度解释了如何调整权重向量使其与一类点形成锐角，与另一类点形成钝角，直至达到理想的分类效果。
接着上篇笔记，这里详细理解一下PLA
- 先回顾下，现在令sign函数=0，在二维图中可以得到一条直线用于分割，现在就是要不断的修正这条线直到它能完美分割图上的两类点，也就是要不断的修正权重向量W来不断接近目标函数f.
- W⃗⋅X⃗=0\vec W\cdot\vec X=0W⋅X=0说明了W与X是垂直的，这样理解，W的维度数量与X维度数量是一致的，以二维为例，w(w1,w2)w(w_1,w_2)w(w1,w2)和x(x1,x2)x(x_1,x_2)x(x1,x2)就是图中的点，所有的线都过原点，现在把图的中心位置定为原点。假定w的一组取值落在x1x_1x1，原点与x1x_1x1点连线得到下图中的紫线，那么满足WX=0的所有x(x1,x2)x(x_1,x_2)x(x1,x2)就全部落在过原点且垂直于紫色线的直线上，下图未画出。
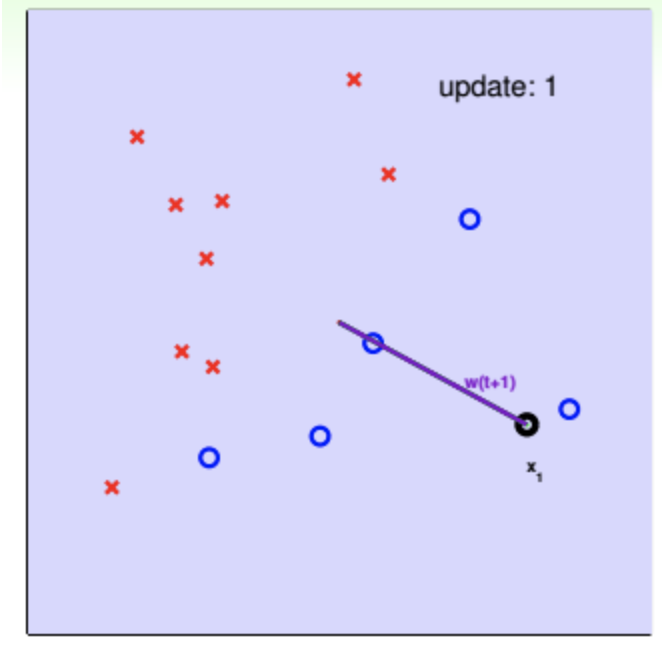
- 一条线画错后修正的方法
wt+1←wt+xw_{t+1}\gets w_t+xwt+1←wt+x
wt+1←wt−xw_{t+1}\gets w_t-xwt+1←wt−x
引入y成为x的系数，合并为wt+1←wt+yxw_{t+1}\gets w_t+yxwt+1←wt+yx
从几何上可以看成，w向量要旋转成与一类点全部成锐角，与另一类点全部成钝角
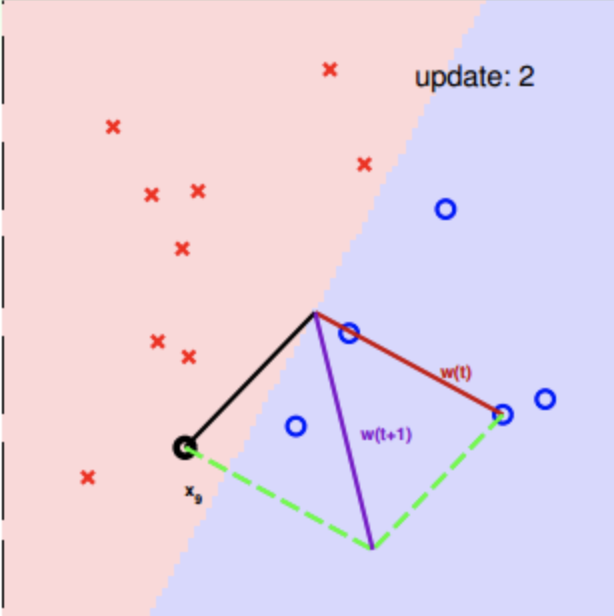
知错能改，wt+x9→wt+1w_t+x_9\to w_{t+1}wt+x9→wt+1
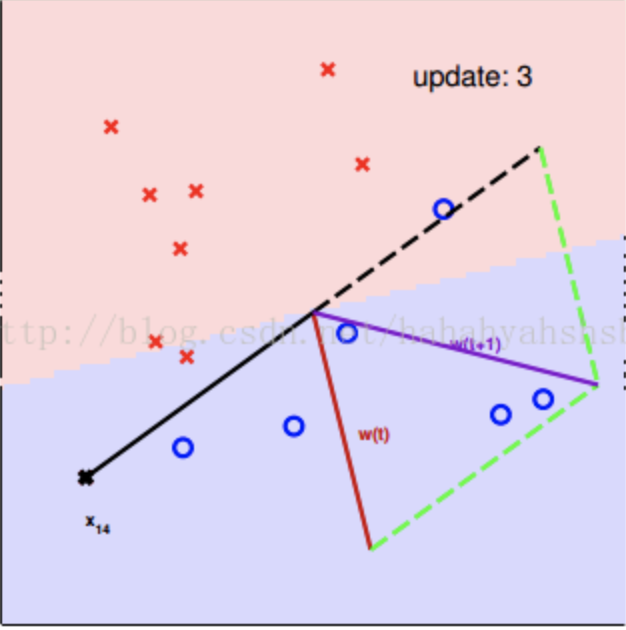
知错能改，wt−x14→wt+1w_t-x_{14}\to w_{t+1}wt−x14→wt+1
注意红蓝分界线也就是h始终与w垂直
如此循环，直到最终完美分类
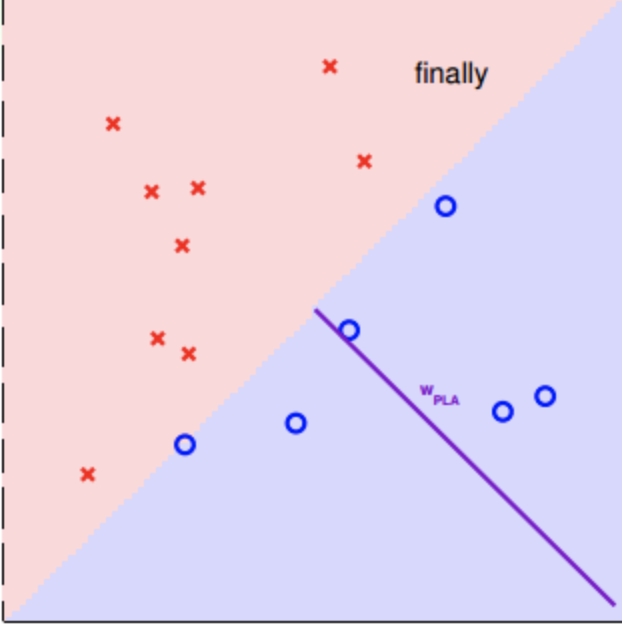
此时确定的w就是最终的wplaw_{pla}wpla
扫一扫
351
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
