Day35 贪心算法part02

贪心算法part02

LC122买卖股票的最佳时机II（未掌握）

1. 未掌握原因分析：对贪心思维转换不过来
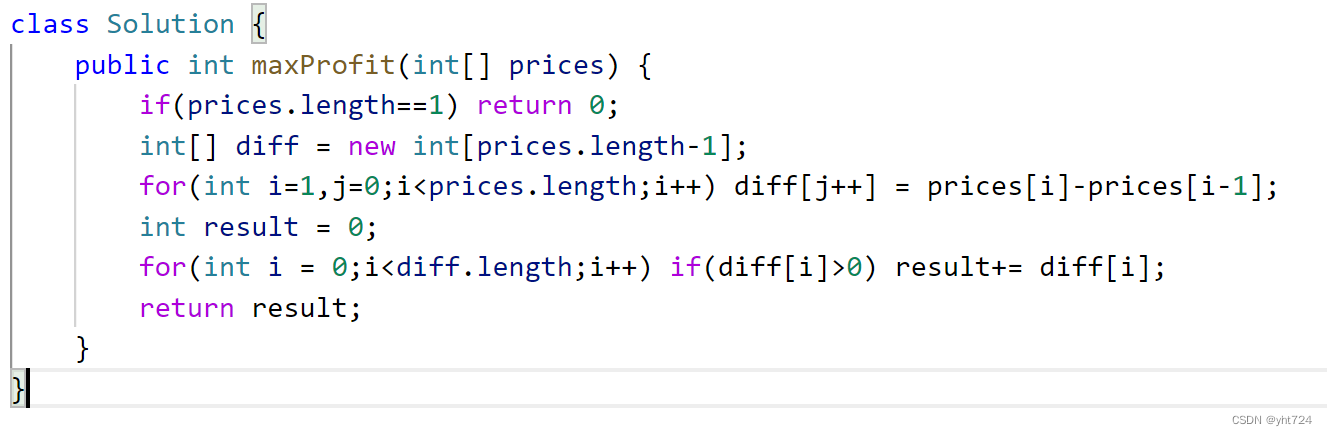
2. 思路：最终利润是可以分解的
   • 第 0 天买入，第 3 天卖出，那么利润为：prices[3] - prices[0]
   • 利润可以分解为(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])
   • 把利润分解为每天为单位的维度，而不是从 0 天到第 3 天整体去考虑，追求每天利润的最大化
   • 然后收集正利润的和即是最大利润值
3. 

LC55跳跃游戏(贪心算法未掌握)

1. dp思路：倒序，如果dp[i]之后的nums[i]个dp数值中存在能够到达最后一个下标的数值，则i位置也可以到达
2. 代码
   
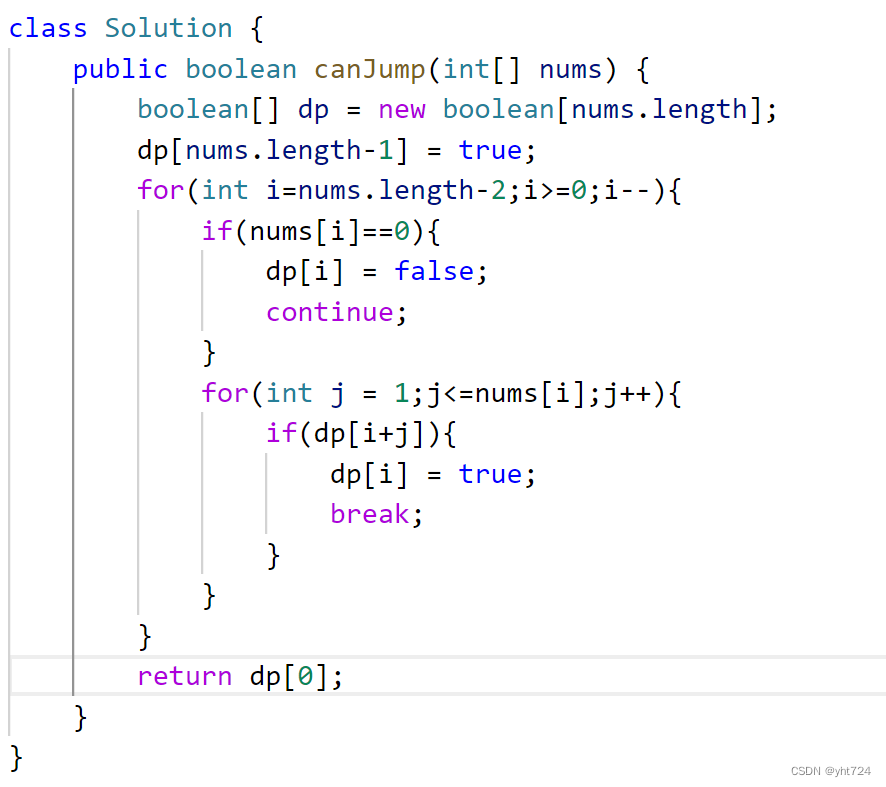
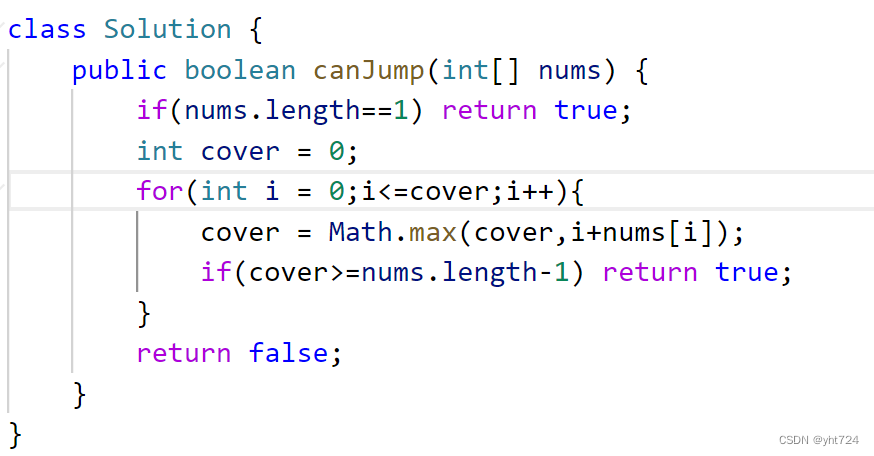
3. 贪心思路：其实每个位置跳几步无所谓，关键在于可跳的覆盖范围，只要每一步的都更新最大范围并且最大范围可以覆盖到终点就说明是可以移动到终点的。
   • 定义for循环，i只能在cover中移动
4. 代码
   

LC45跳跃游戏II(未掌握)

1. 贪心思路：
   • 从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最少步数
   • 移动下标达到了当前覆盖的最远距离下标时，步数就要加一，来增加覆盖距离。最后的步数就是最少步数。
2. 代码
   • curDistance：当前覆盖最远距离下标
   • nextDistance：当前范围中找到的下一个覆盖最远距离下标
     
3. 动态规划
   • dp表示从下标i到nums.length-1所需的最小步数
   • 初始化，dp[nums.length-1]=Integer.MAX_VALUE，因为涉及后序求min，所以初始化为最大值
   • 递推方程
     • 如果i+j（从1到nums[i]）会超过nums.length-1，直接dp[i]=1
     • 如果dp[i+j]!=Integer.MAX_VALUE，说明i+j位置可以到达nums.length-1，步数+1即可，然后在循环中不断取最小值
   • 代码
     

LC1306跳跃游戏III(未掌握)

1. DFS：前序递归，从根节点开始
2. 代码
   • 一开始以为使用回溯，但是used数组是不需要回溯的，往加走还是往减走都是不用回溯的
     

LC1871跳跃游戏IV(未掌握)

1. boolean[] result表示下标i位置的元素是否可达
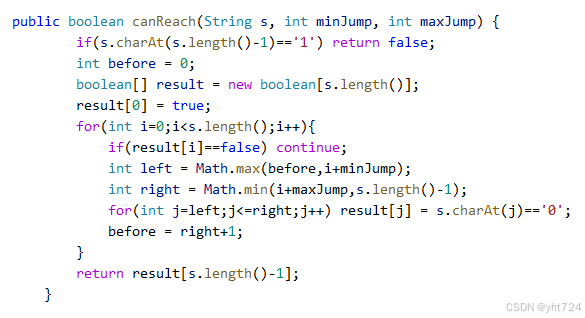
2. 对于i来说，判断的位置是i + minJump <= = > min(i + maxJump, s.length - 1)，但是下一个可达的j判断的是j + minJump <= = >min(j + maxJump, s.length - 1)，两者可以剪枝处理，采用before记录上一个最远可达的下一个位置，即Math.max(before,i+minJump)<= = > min(i + maxJump, s.length - 1)
3. 对于i+1 < = = > left 通过判断字符是否为0来判断是否可达
4. 代码
   
5. 采用dp数组表示i是否可达s.length()-1将导致超时，无法使用上法类似的剪枝，因为不存在范围上重叠的部分可以免除判断的情况，上法是因为dp[i]是根据s.charAt(j)位置的字符判断的而不是dp[i+xxx]
6. 代码
   • 哪怕是改成if(s.charAt(j)=‘0’)也是会有问题的，因为dp数组的含义是i能否到达s结尾，就算当前位置是0也可能到达不了s结尾，仅仅靠s.charAt(j)=='0’是不可靠的