Day11 栈与队列part02

第十一天 栈与队列part02

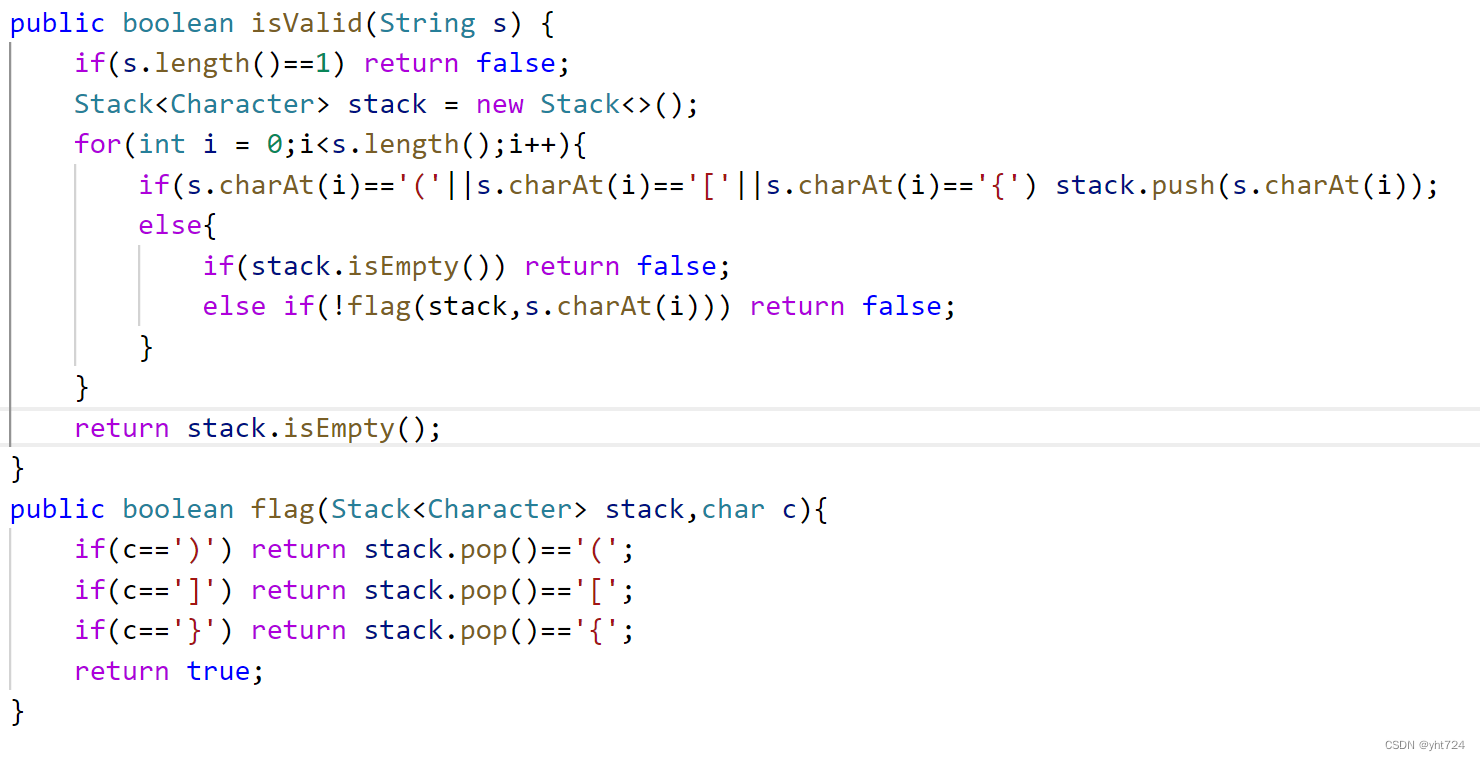
LC20有效的括号

1. 代码：
   
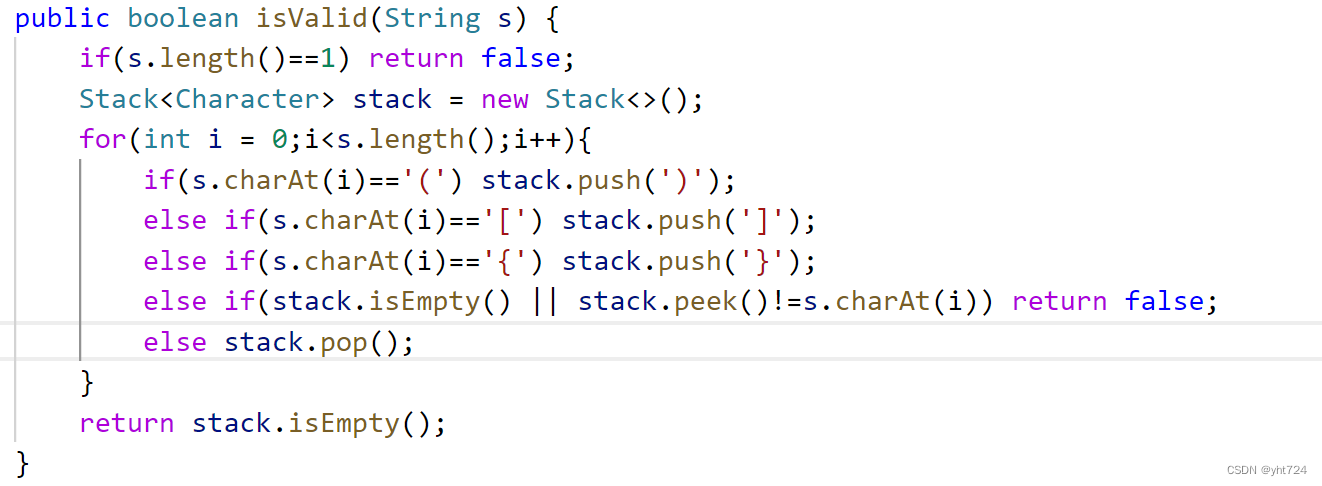
2. 更为简洁的代码
   • 遍历过程中每次碰到左括号栈就入栈对应的右括号
   • 当碰到右括号判断出栈元素是否等于右括号，不等则直接return false
   • 当栈为空说明右括号多了，return false
   • 最后如果栈不为空也return false，说明左括号多了
     

LC1047删除字符串中的所有相邻重复项

1. 代码
   
2. 减少空间复杂度：使用字符串的拼接操作，原本栈中字符的逆序直接使用字符串的拼接解决：
   

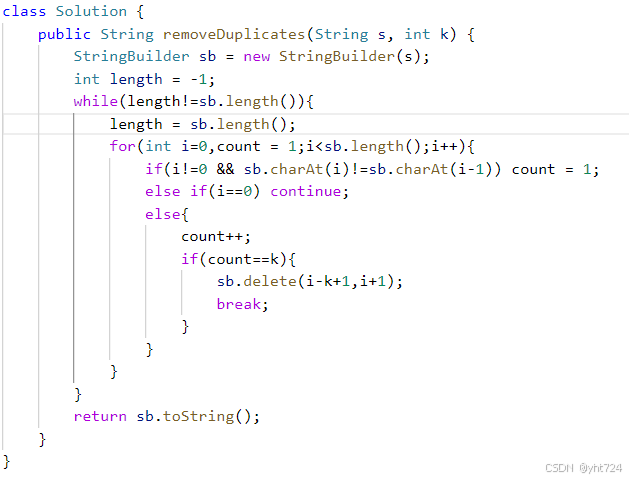
LC1209删除字符串中的所有相邻重复项II(未掌握)

1. 暴力方法：
   • 对相邻元素进行计数，如果相同就计数+1，反之计数维持在1
   • 当计数等于k的时候，就需要删除掉k个相同的元素
   • 需要两个循环，每一次都需要从i=0进行判断，因为删除掉元素之后可能更前序元素组成k个相同的元素
   • 外层循环使用长度来进行判断，因为满足条件需要进行删除元素，当长度始终不变即整个字符串完成了处理
   • 代码
     
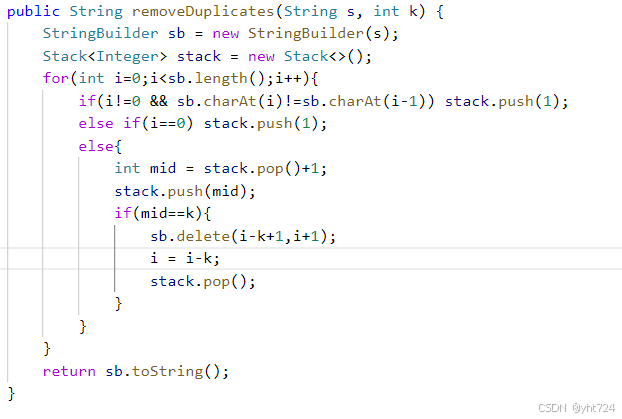
2. 使用栈
   • 使用栈对暴力算法进行时间上的优化，因为暴力需要在外层循环保持一个不断变化的length，使用栈来简化
   • 栈中当前字符与前一个不同时，往栈中压入 1。否则栈顶元素加 1
   • 当栈顶元素等于k的时候，就需要删除一些元素，然后i下标需要前移
   • 代码
     

LC150逆波兰表达式（超时5min）

1. 超时分析：

   • 字符串判断相等应该用equals，而不是equal和==

2. 代码：
   

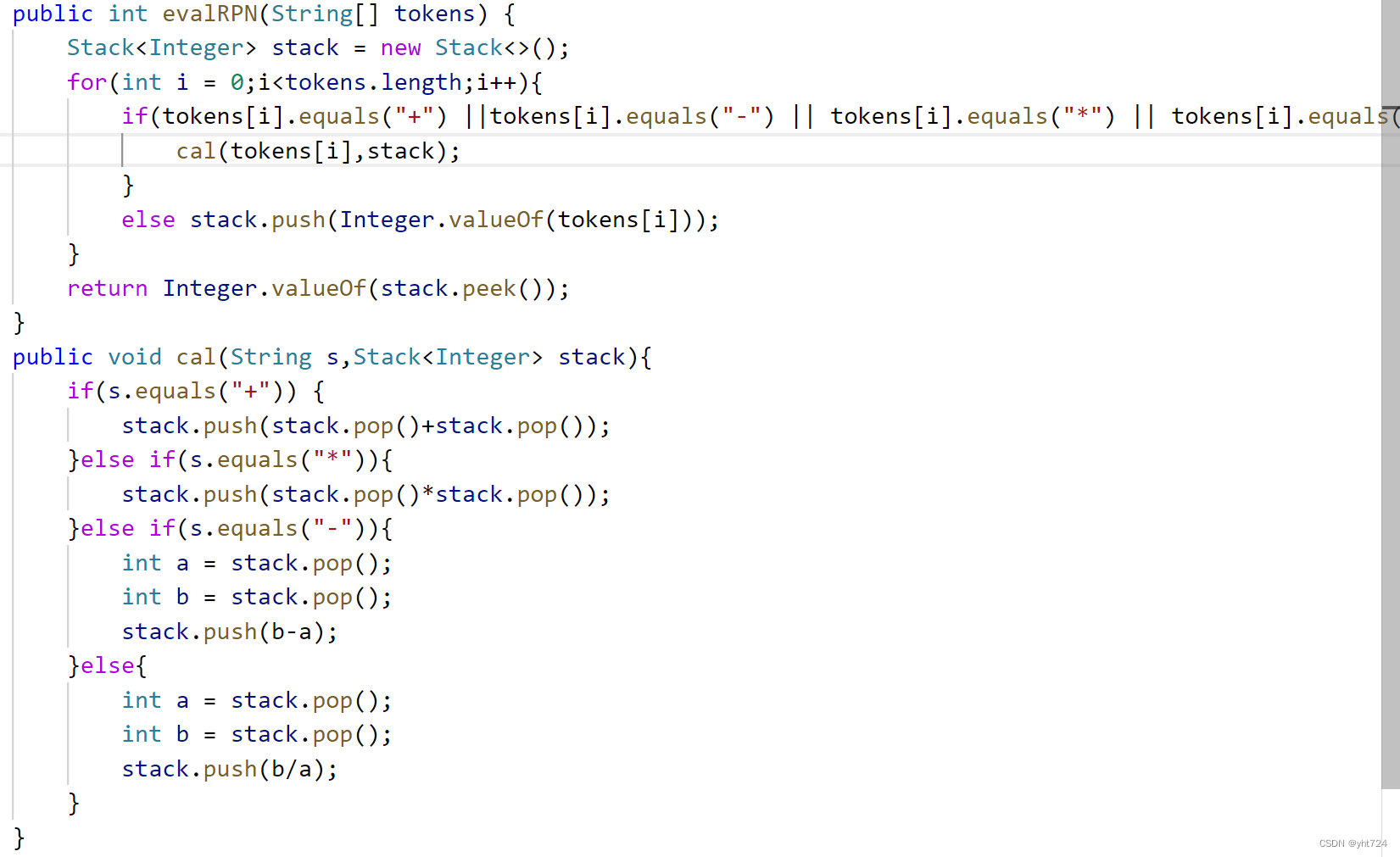
3. 知识点

   • 我们平常所熟知的算式是中缀表达式，但是中缀表达式因为运算符的优先级对计算机运算并不是很友好
   • 逆波兰表达式，其实就是一种后缀表达式
   • 后缀表达式的优点：
     • 去掉括号后表达式无歧义，(1+2)*(3+4)=》((12+)(34+)*)=》12+34+*
     • 适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中

4. 难点：中缀表达式转后缀表达式

   • 准备一个栈用来存放操作符和括号，准备一个数组用来存放数字和弹出的字符
   • 遇到操作数，直接存储在数组中
   • 遇到操作符
     • 栈为空、该操作符的优先级比栈顶的操作符的优先级高（该操作符需要先运算，根据栈的后入先出，肯定是入栈放在栈顶之后）=》压栈
     • 该操作符的优先级比栈顶的操作符优先级低 or 相同=》弹出栈顶操作符存储，并将该操作符压栈
   • 遍历结束后将栈里的操作符依次全部弹出，依次存储在数组末尾
   • 括号的处理：一个括号就相当于一个独立的式子
     • 遇见左括号=》左括号入栈
     • 遇到操作符=》栈为空、该操作符的优先级比栈顶的操作符的优先级高、如果栈顶为左括号(类比于栈为空的情况)=》压栈
     • 遇到右括号=》弹出栈中的操作符直到遇到左括号（左括号出栈但不存储）
   • 负数的处理：负数会对处理造成影响只可能是负数出现在开头（1. 表达式的开头：-1+5*3。2.括号子式的开头：3+(-6)/2）其他情况都看作是-
     • 处理：遇到负数时首先存储一个0，这样就可以通过减法来模拟负数

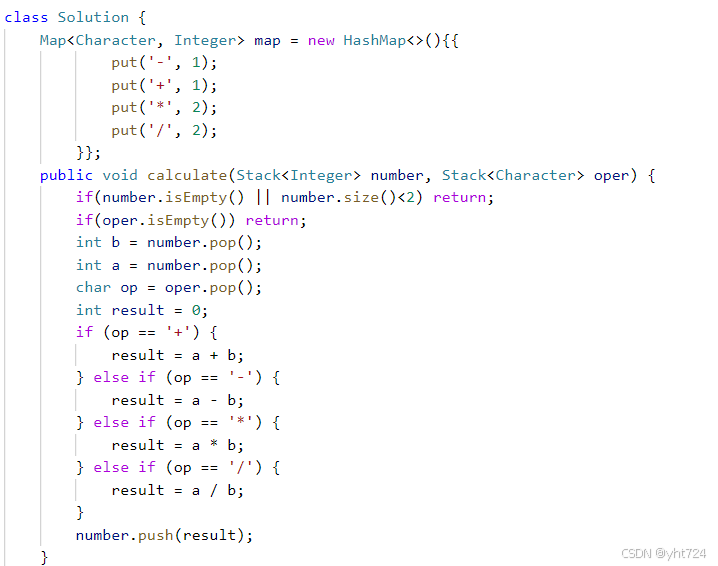
5. LC224基本计算器

   • 使用字典维护一个符号优先级
   • 由于第一个数可能是负数，为了减少边界判断。一个小技巧是先往 nums 添加一个 0
   • 分为四种情况：（、）、数字、字符
     • （：入栈
     • ）：符号栈中能计算的计算完
     • 数字：多个数字连在一起作为一个整体
     • 符号：防着（-、±、–【其中）-已经被涵盖、*-和/-本身不合法】看情况添加0。将符号栈中优先级大于等于的能计算计算完
   • 代码