树 226. 翻转二叉树 617.合并二叉树 101. 对称二叉树

最新推荐文章于 2025-09-05 21:19:19 发布

原创最新推荐文章于 2025-09-05 21:19:19 发布 · 168 阅读

0 ·

CC 4.0 BY-SA版权

Leetcode 同时被 2 个专栏收录

26 篇文章

订阅专栏

树

5 篇文章

订阅专栏

本文深入探讨了二叉树的三种经典操作：翻转、合并和对称性判断。通过递归和迭代两种方法，详细解析了算法实现，并附带代码示例，帮助读者理解并掌握二叉树相关算法。

226. 翻转二叉树

翻转一棵二叉树。

示例：

输入：
     4
   /   \
  2     7
 / \   / \
1   3 6   9

输出：
     4
   /   \
  7     2
 / \   / \
9   6 3   1

思路1：递归

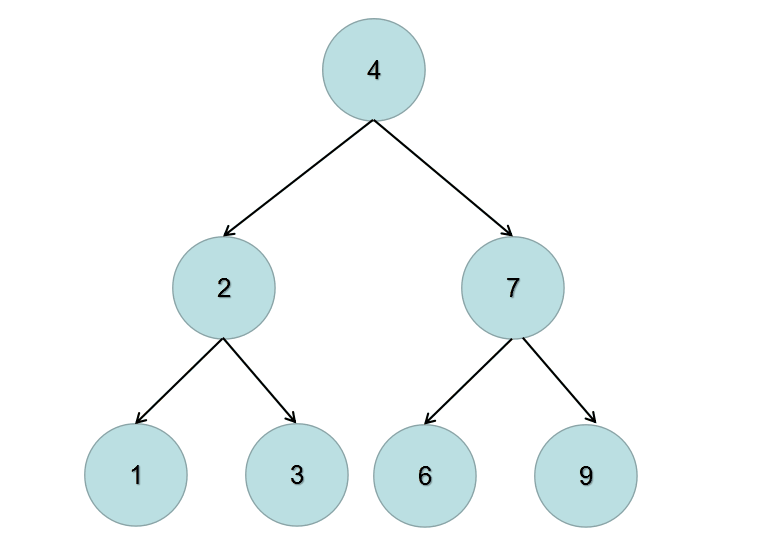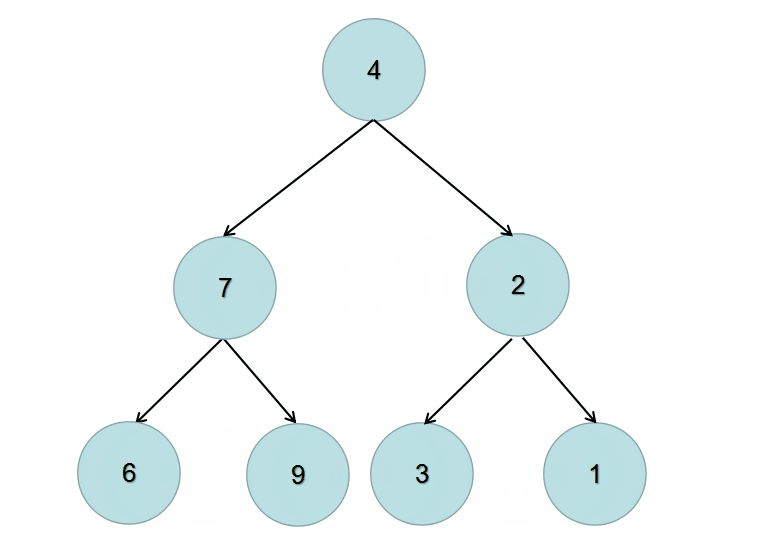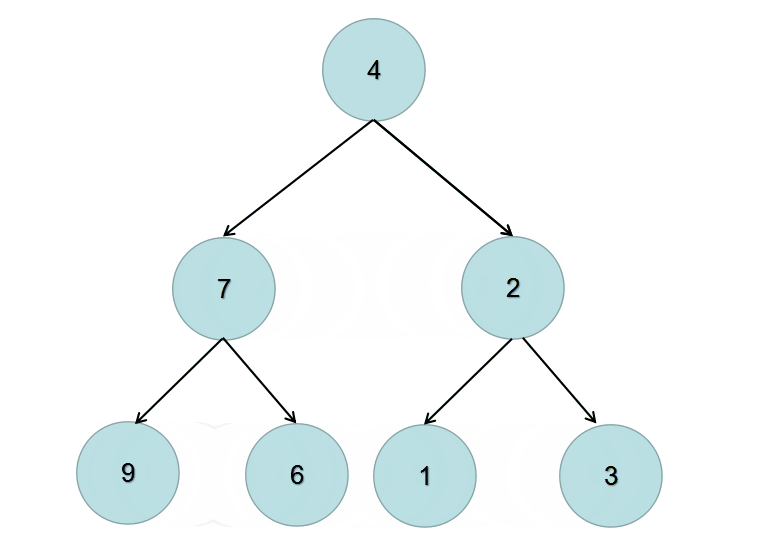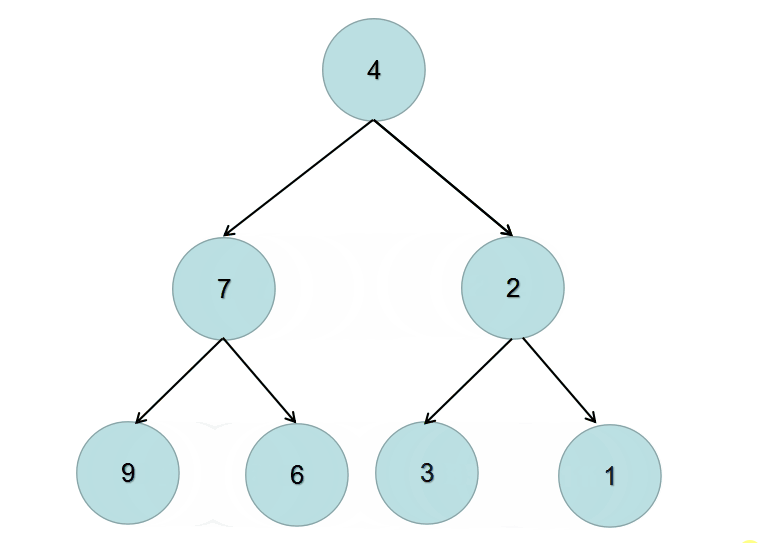
在这里插入图片描述
根据动画图我们可以总结出递归的两个条件如下：

终止条件：

当前节点为null时返回
交换当前节点的左右节点，再递归的交换当前节点的左节点，递归的交换当前节点的右节点

时间复杂度：每个元素都必须访问一次，所以是O(n)
空间复杂度：最坏的情况下，需要存放O(h)个函数调用(h是树的高度)，所以是O(h)

代码实现1：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
    	# 递归函数的终止条件，节点为空时返回
        if root is None:
            return root
        # 将当前节点的左右子树交换
        root.left, root.right = root.right, root.left
        # 递归交换当前节点的 左子树和右子树
        self.invertTree(root.left)
        self.invertTree(root.right)
		# 函数返回时就表示当前这个节点，以及它的左右子树都已经交换完了
        return root

思路2：迭代

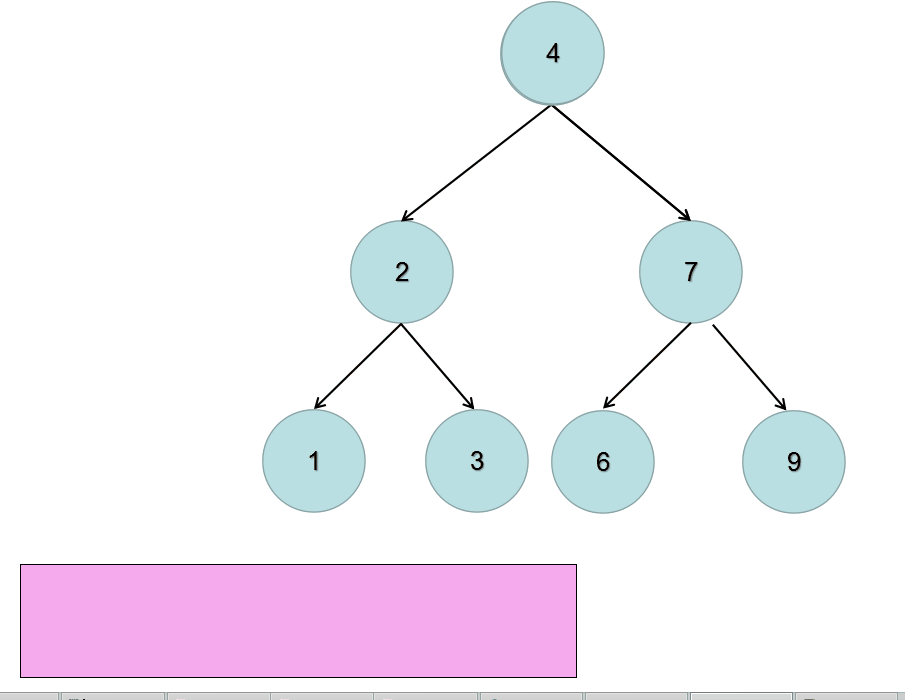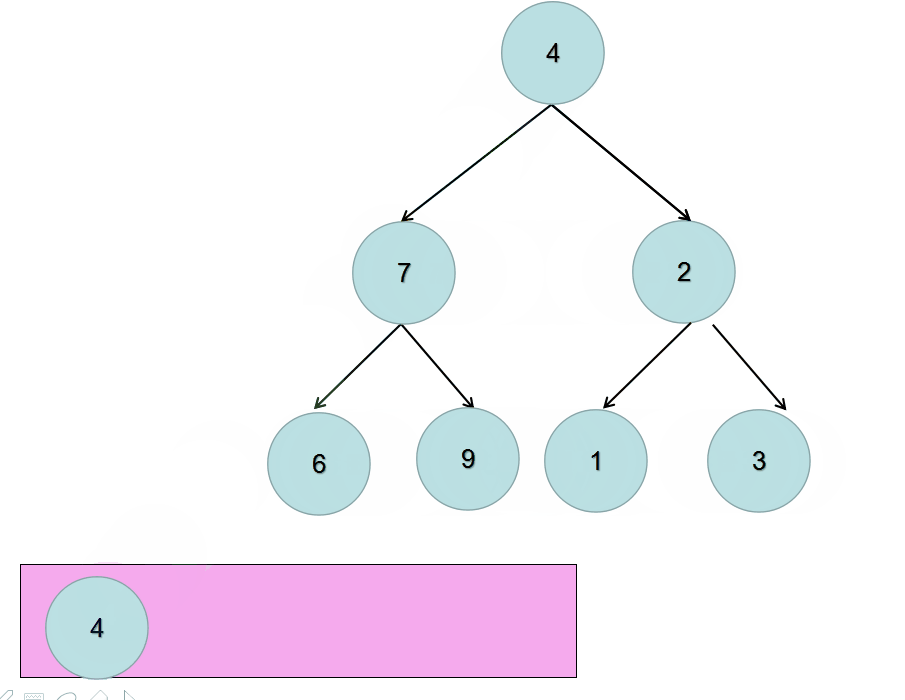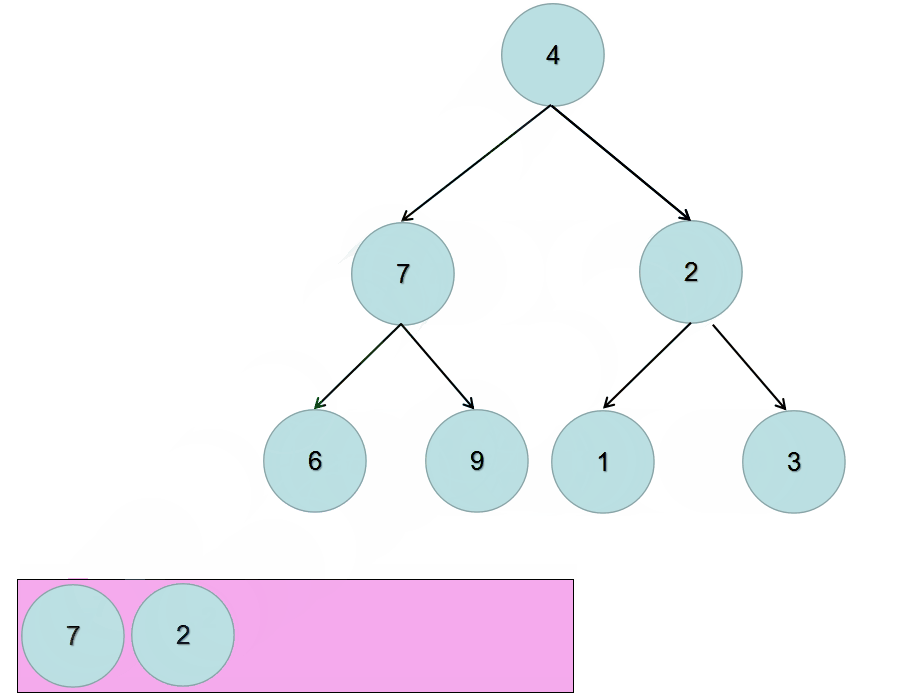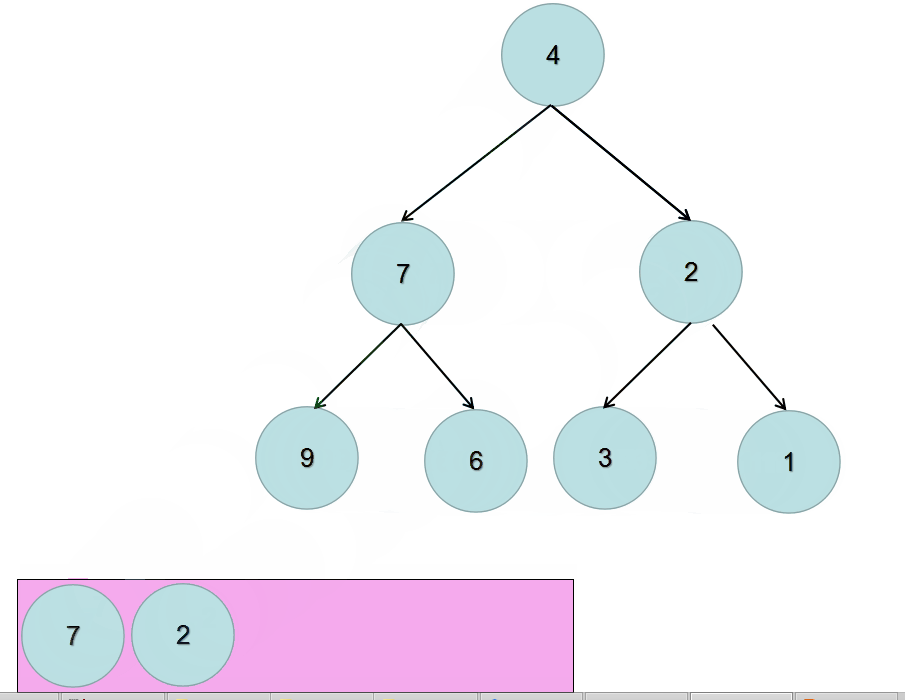
在这里插入图片描述
递归实现也就是深度优先遍历的方式，那么迭代对应的就是广度优先遍历。
广度优先遍历需要额外的数据结构–队列，来存放临时遍历到的元素。
深度优先遍历的特点是一竿子插到底，不行了再退回来继续；而广度优先遍历的特点是层层扫荡。
所以，我们需要先将根节点放入到队列中，然后不断的迭代队列中的元素。
对当前元素调换其左右子树的位置，然后：

判断其左子树是否为空，不为空就放入队列中
判断其右子树是否为空，不为空就放入队列中

代码实现2：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if root is None:
            return root
        queue = [root]
        while queue:
            cur = queue.pop(0)
            cur.right, cur.left = cur.left, cur.right
            if cur.left:
            	queue.append(cur.left)
            if cur.right:
                queue.append(cur.right)
                
        return root

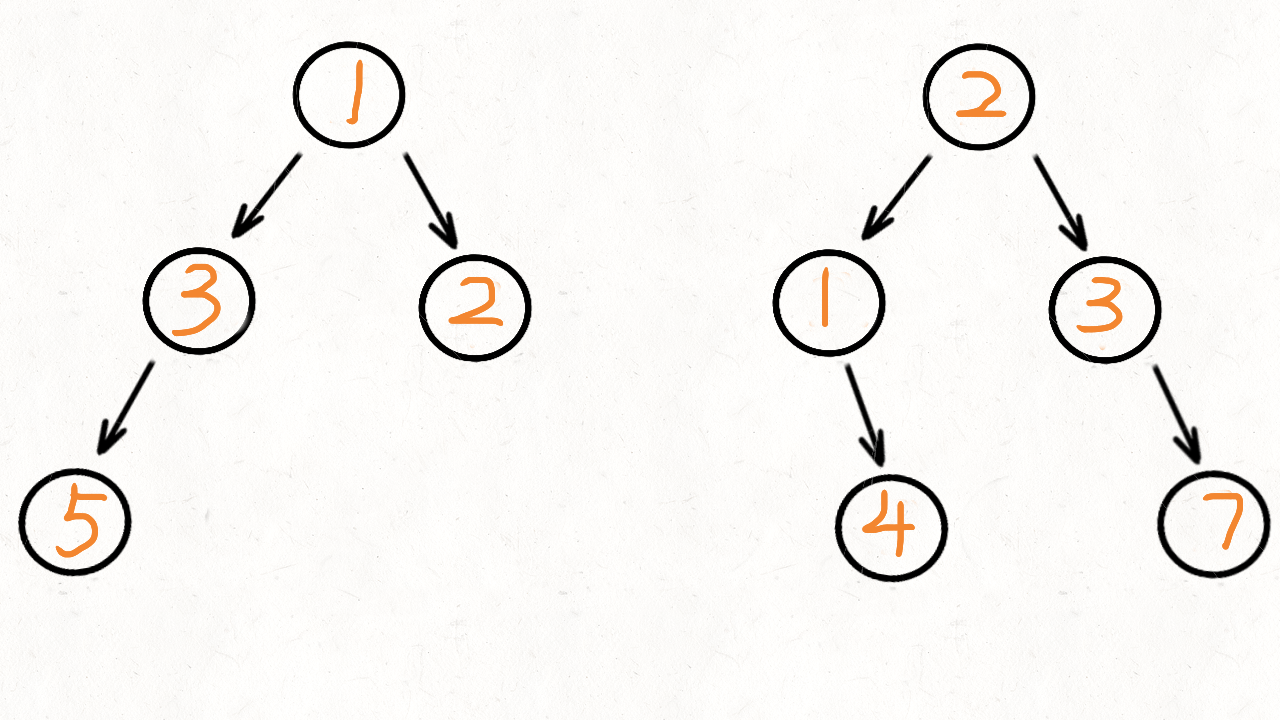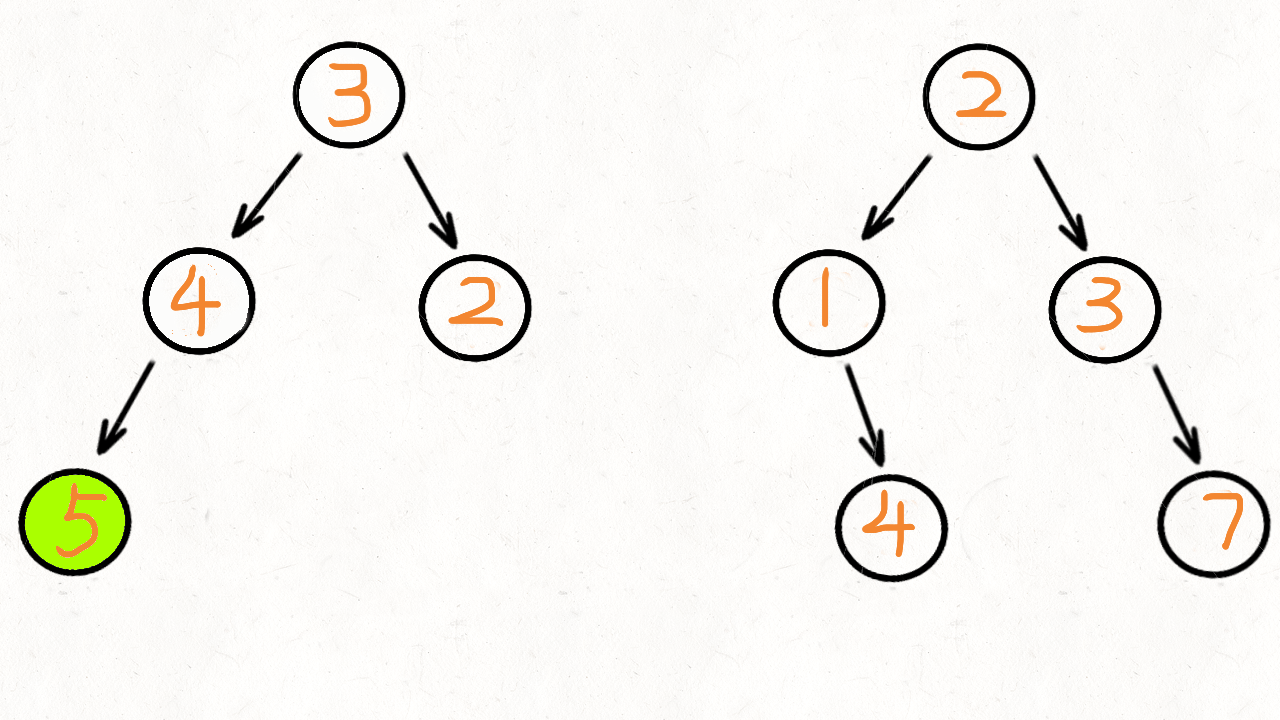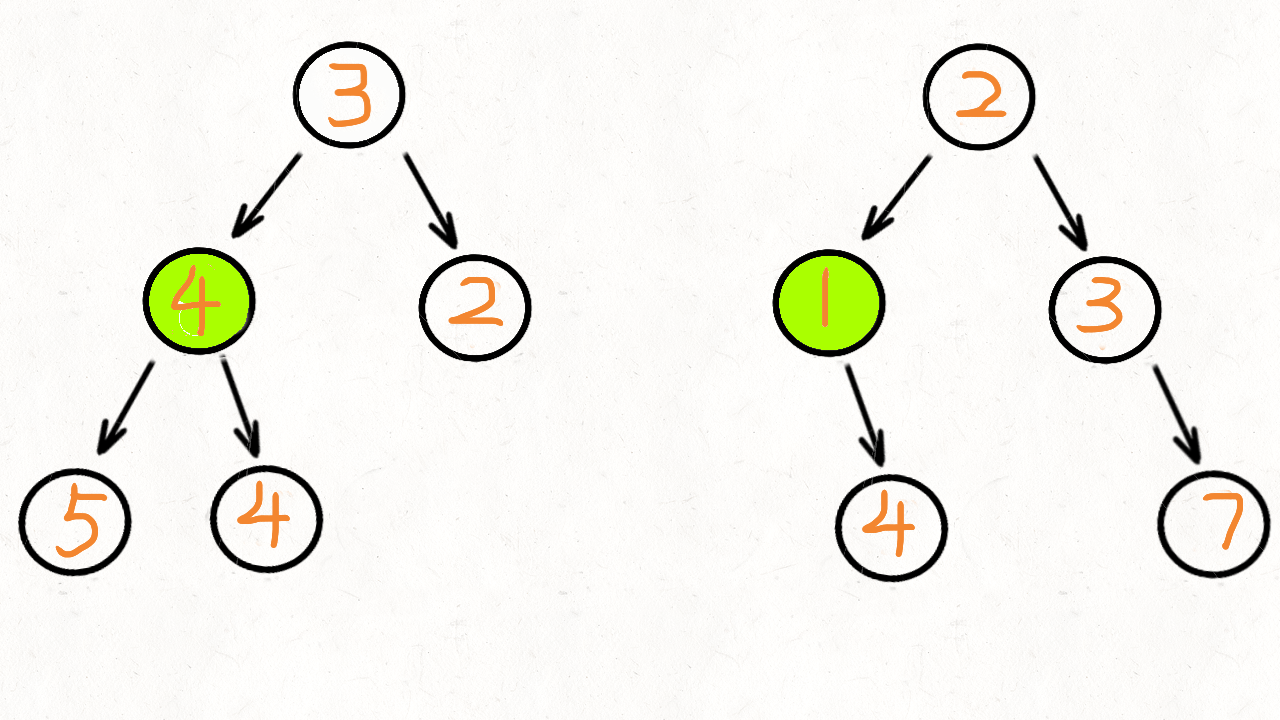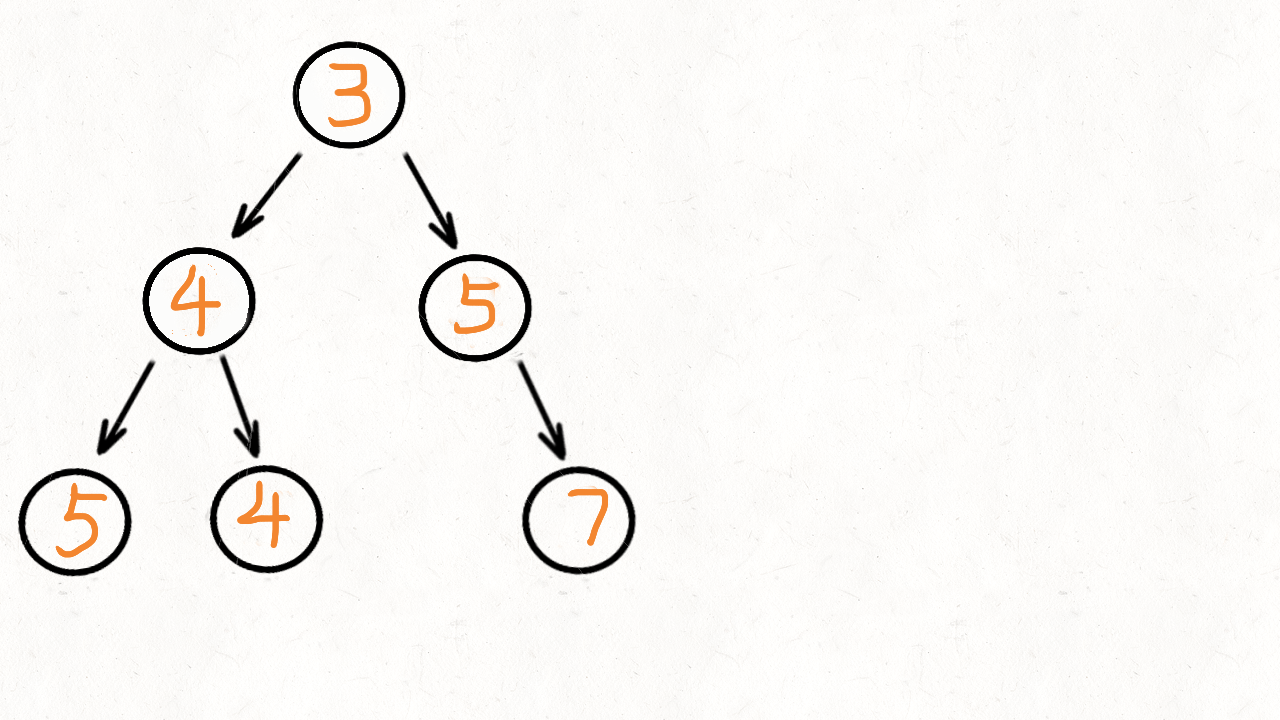
617. 合并二叉树

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例：

输入: 
	Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
      
输出: 
合并后的树:
	     3
	    / \
	   4   5
	  / \   \ 
	 5   4   7

思路1：递归

用前序遍历，依次把访问到的节点值相加，因为题目没有说不能改变树的值和结构，我们不用再创建新的节点了，直接将树2合并到树1上再返回就可以了。
递归的条件：

终止条件：树1的节点为null，或者树2的节点为null
递归函数内：将两个树的节点相加后，再赋给树1的节点。再递归的执行两个树的左节点，递归执行两个树的右节点

在这里插入图片描述

代码实现1：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
        if not (t1 and t2):
            return t1 if t1 else t2
        t1.val += t2.val
        t1.left = self.mergeTrees(t1.left, t2.left)
        t1.right = self.mergeTrees(t1.right, t2.right)

        return t1

思路2：迭代

迭代实现用的是广度优先算法，广度优先就需要额外的数据结构来辅助了，我们可以借助栈或者队列来完成。
只要两颗树的左节点都不为null，就把将他们放入队列中；同理只要两棵树的右节点都不为null了，也将他们放入队列中。
然后我们不断的从队列中取出节点，把他们相加。
如果出现树1的left节点为null，树2的left不为null，直接将树2的left赋给树1就可以了；同理如果树1的right节点为null，树2的不为null，将树2的right节点赋给树1。
在这里插入图片描述

代码实现：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
        if not (t1 and t2):
            return t1 if t1 else t2
        queue = [(t1, t2)]
        while queue:
            r1, r2 = queue.pop(0)
            # 先将值相加
            r1.val += r2.val
            
            # 如果r1和r2的左子树都不为空，就放到队列中
            if r1.left and r2.left:
                queue.append((r1.left, r2.left))
            # 如果r1和r2的右子树都不为空，就放到队列中
            if r1.right and r2.right:
                queue.append((r1.right, r2.right))
            # 如果r1左子树为空，就把r2的左子树挂到r1的左子树上
            if not r1.left:
                r1.left = r2.left
            # 如果r1右子树为空，就把r2的右子树挂到r1的右子树上
            if not r1.right:
                r1.right = r2.right

        return t1

101. 对称二叉树

思路1：递归

镜像对称，就是左右两边相等，即左子树和右子相等，也就是说要递归的比较左子树和右子树。
我们将根节点的左子树记做left，右子树记做right。比较left是否等于right，不等的话直接返回就可以了。
如果相当，比较left的左节点和right的右节点，再比较left的右节点和right的左节点
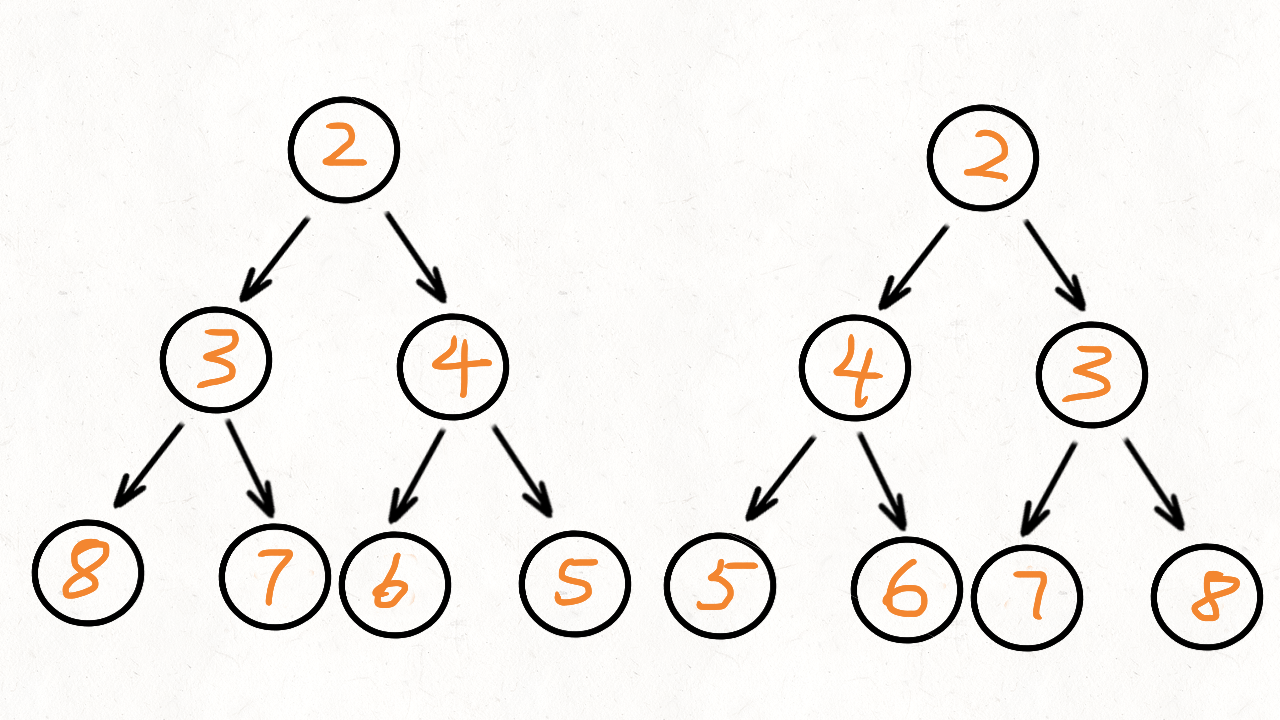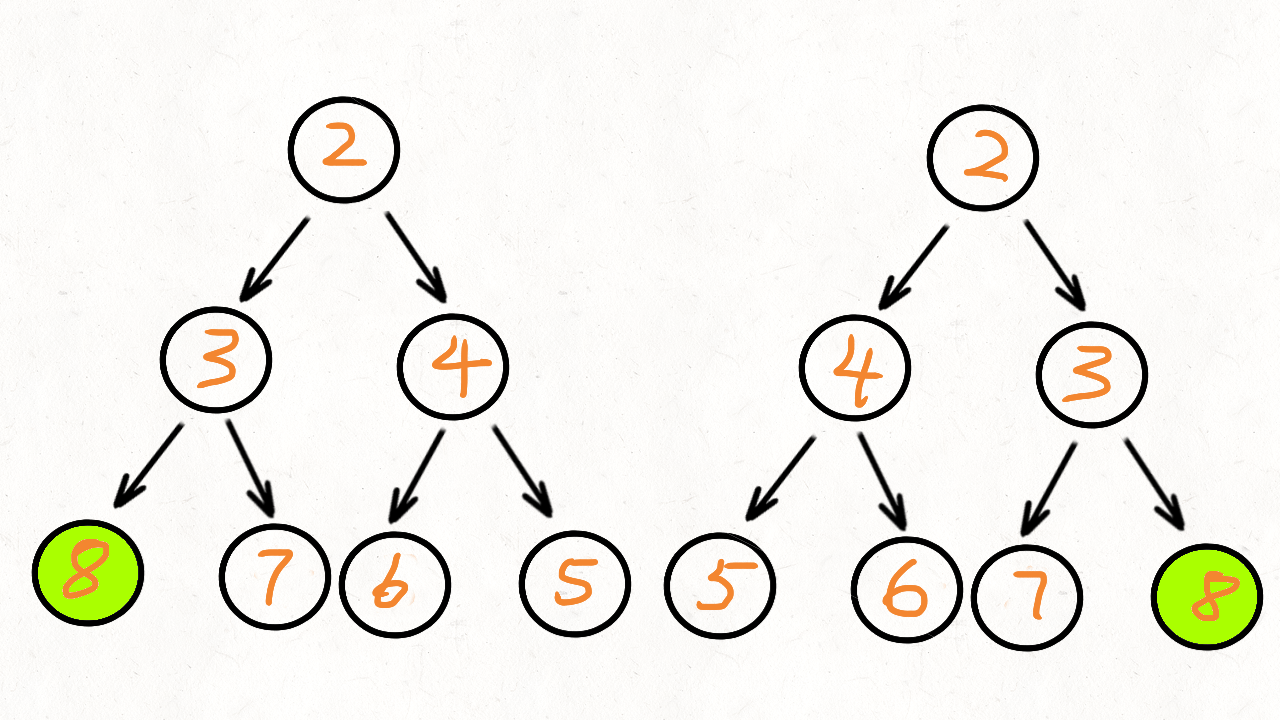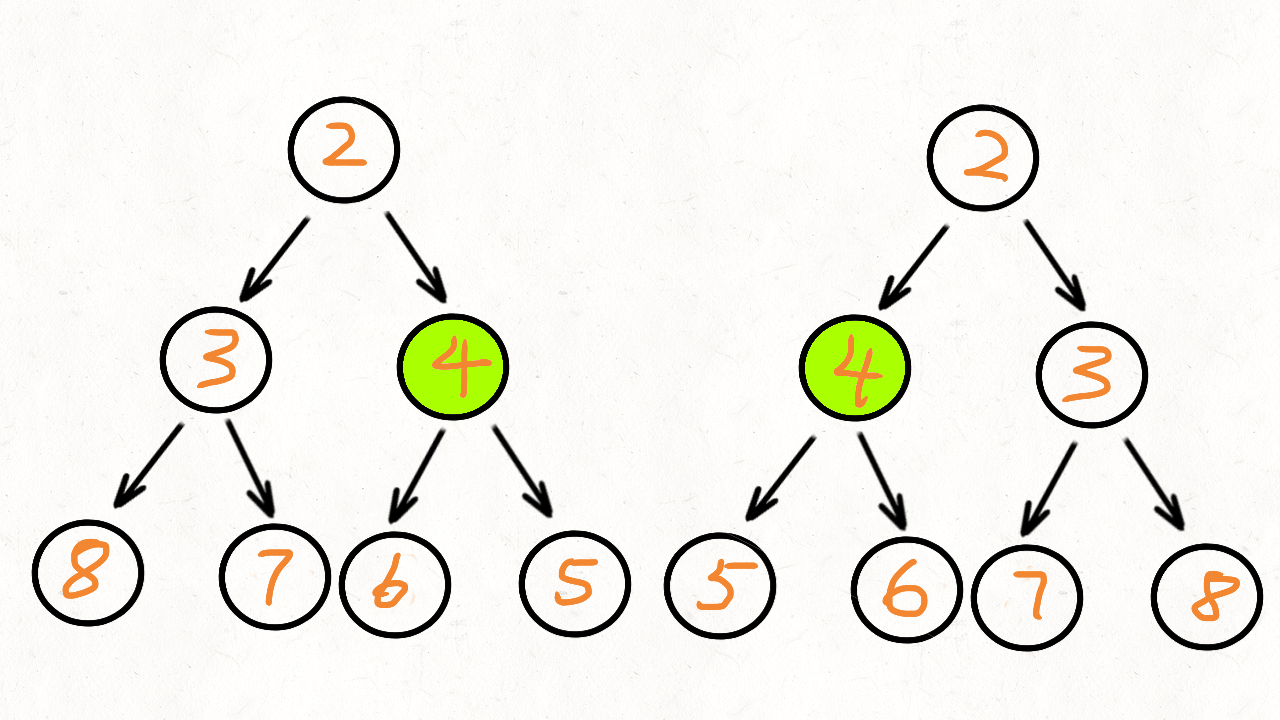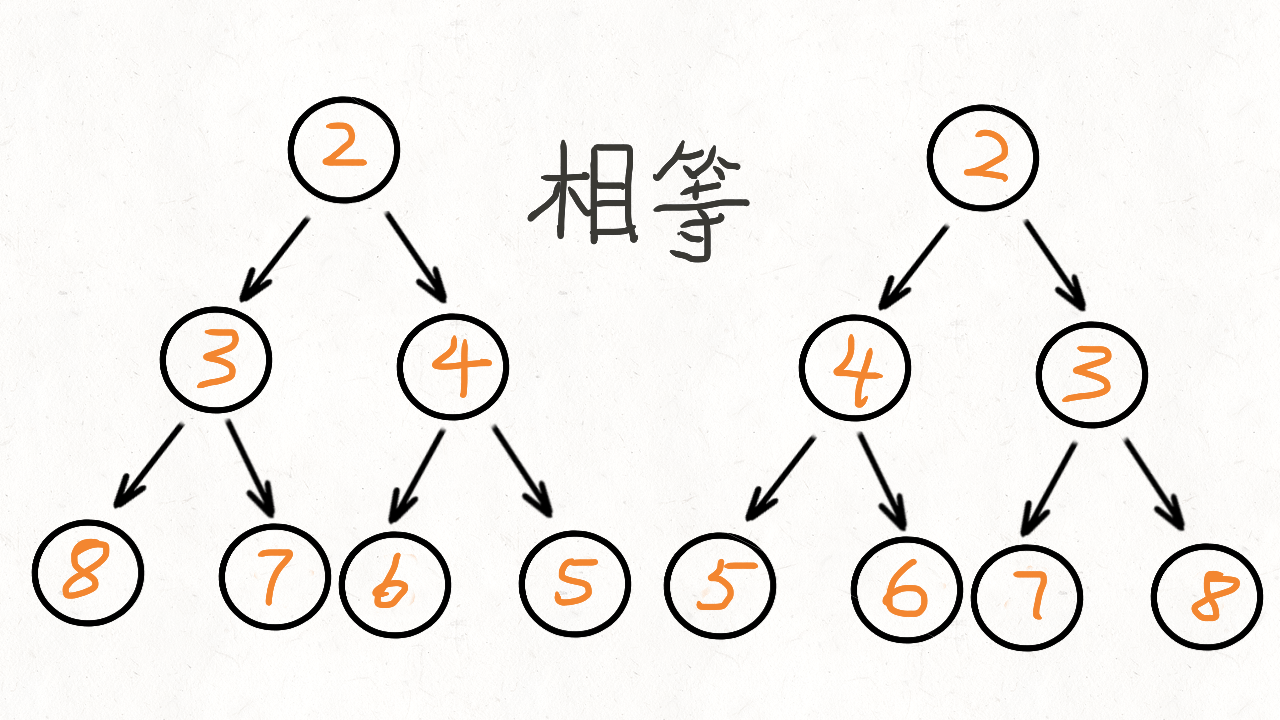
比如看下面这两个子树(他们分别是根节点的左子树和右子树)，能观察到这么一个规律：
左子树2的左孩子 == 右子树2的右孩子
左子树2的右孩子 == 右子树2的左孩子

    2         2
   / \       / \
  3   4     4   3
 / \ / \   / \ / \
8  7 6  5 5  6 7  8

根据上面信息可以总结出递归函数的两个条件：
终止条件：

left和right不等，或者left和right都为空
递归的比较left.left和right.right，递归比较left.right和right.left

代码实现1：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def travel(self, t1, t2):
        # 递归的终止条件是两个节点都为空
        # 或者两个节点中有一个为空
        # 或者两个节点的值不相等
        if not (t1 or t2):
            return True
        if not (t1 and t2):
            return False
        if t1.val != t2.val:
            return False
        return self.travel(t1.left, t2.right) and self.travel(t1.right, t2.left)

    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
		# 用递归函数，比较左节点，右节点
        return self.travel(root.left, root.right)

思路2：迭代

首先从队列中拿出两个节点(left和right)比较
将left的left节点和right的right节点放入队列
将left的right节点和right的left节点放入队列
时间复杂度是O(n)，空间复杂度是O(n)

代码实现2：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True
        queue = [root.left, root.right]
        while queue:
        	# # 从队列中取出两个节点，再比较这两个节点
            left = queue.pop(0)
            right = queue.pop(0)
            # # 如果两个节点都为空就继续循环，两者有一个为空就返回false
            if not (left or right):
                continue
            if not (left and right):
                return False
            if left.val != right.val:
                return False
            # 将左节点的左孩子， 右节点的右孩子放入队列
            queue.append(left.left)
            queue.append(right.right)
            # 将左节点的右孩子，右节点的左孩子放入队列
            queue.append(left.right)
            queue.append(right.left)
        return True