数组/列表 283. 移动零 566.重塑矩阵 485. 最大连续1的个数

最新推荐文章于 2022-06-20 17:13:22 发布

原创最新推荐文章于 2022-06-20 17:13:22 发布 · 305 阅读

0 ·

CC 4.0 BY-SA版权

Leetcode 同时被 2 个专栏收录

26 篇文章

订阅专栏

数组/列表

3 篇文章

订阅专栏

本文深入讲解了移动零、重塑矩阵及最大连续1的个数等经典算法问题的多种解决方案，包括暴力法、两次遍历法、一次遍历法等，通过实例演示了不同算法的实现过程，帮助读者掌握算法设计和优化技巧。

283. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

必须在原数组上操作，不能拷贝额外的数组。
尽量减少操作次数。

示例：

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

思路1：暴力法

遍历列表，遇到零的时候将其移除，并添加到列表末尾

代码实现1：

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        for i in nums:
            if i == 0:
                nums.remove(0)
                nums.append(0)

思路2：两次遍历法

使用两个指针a、b。a向前走，每遇到一个非0元素就将其往移动到指针b处，此时b也向前走一个位置，第一次遍历完后，b指针的下标就指向了最后一个非0元素下标。
第二次遍历的时候，起始位置就从b开始到结束，将剩下的这段区域内的元素全部置为0。
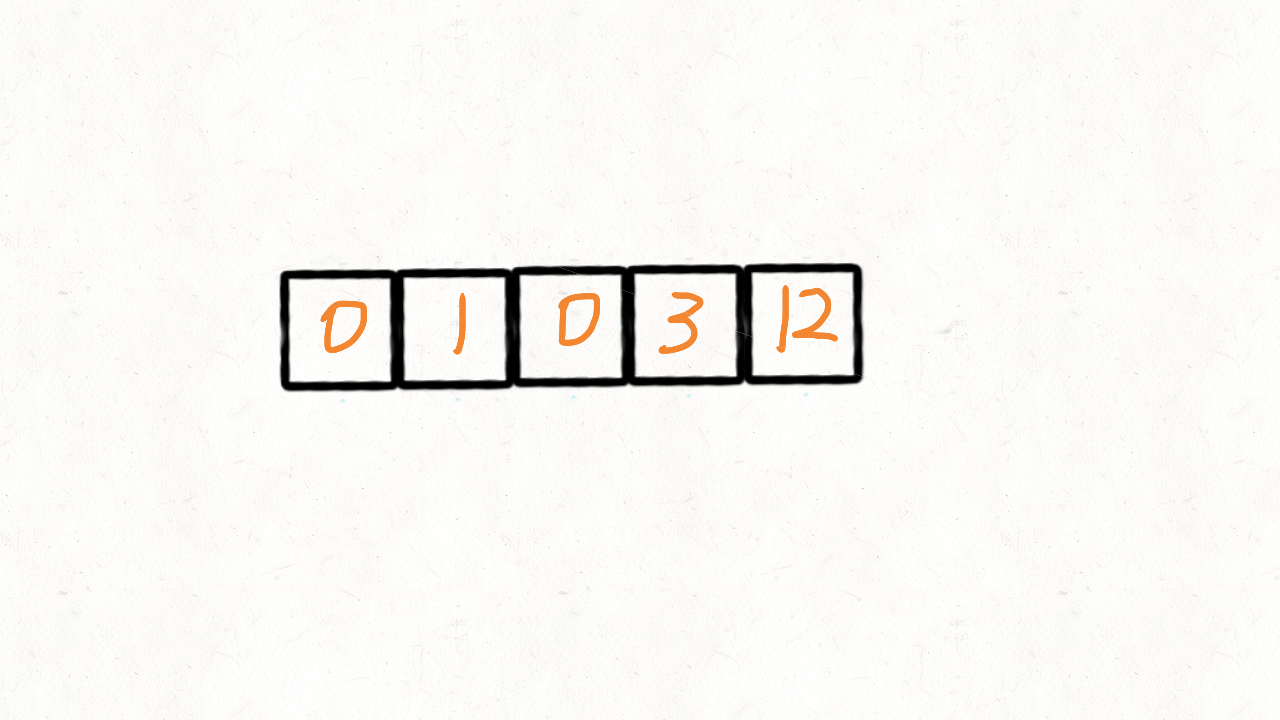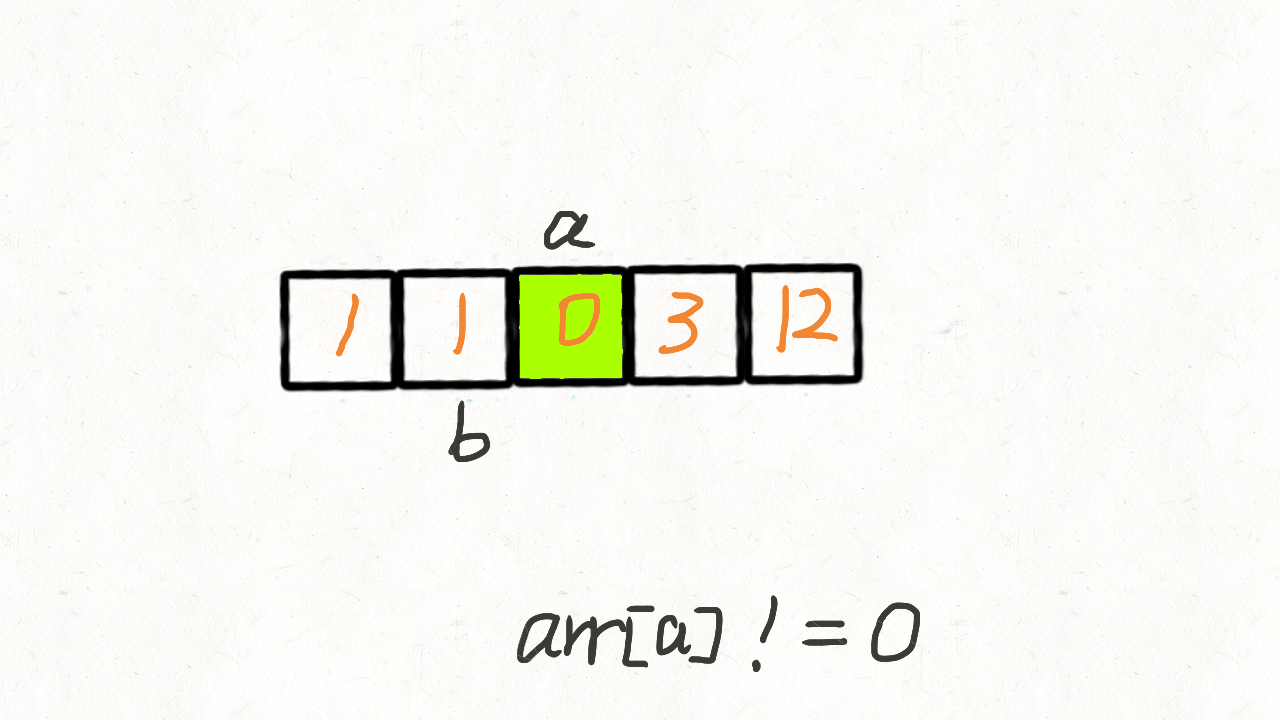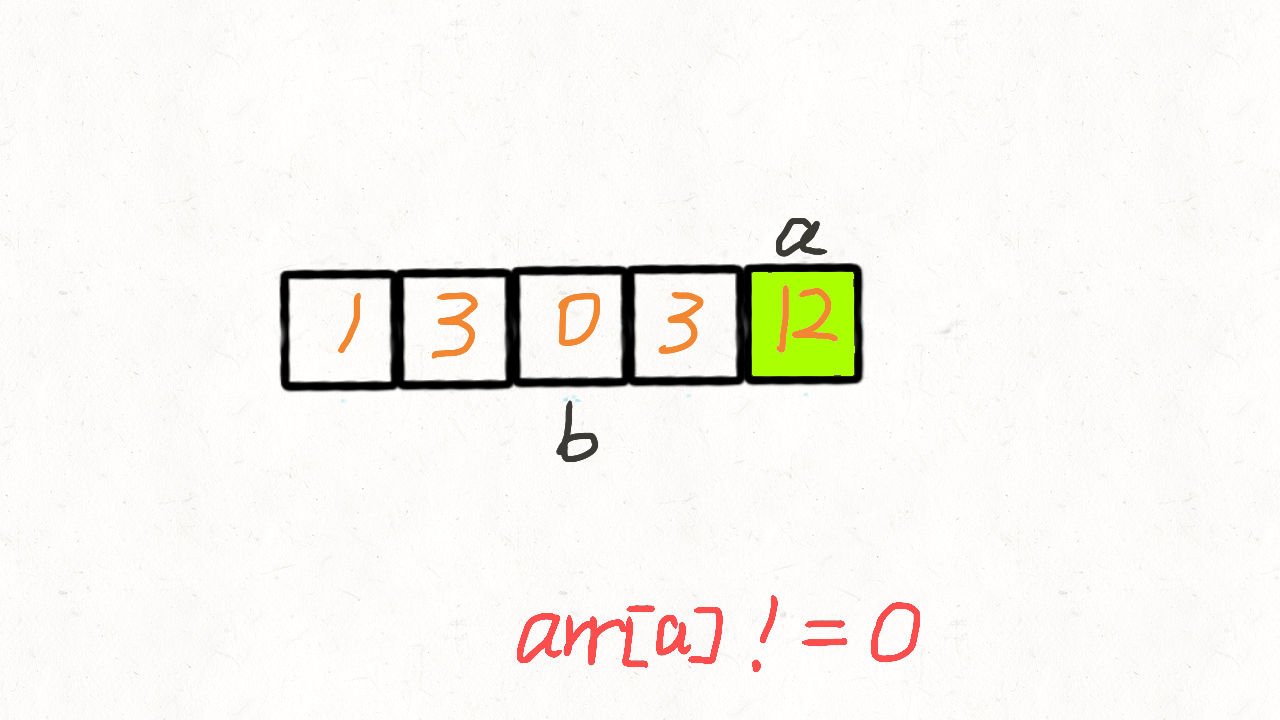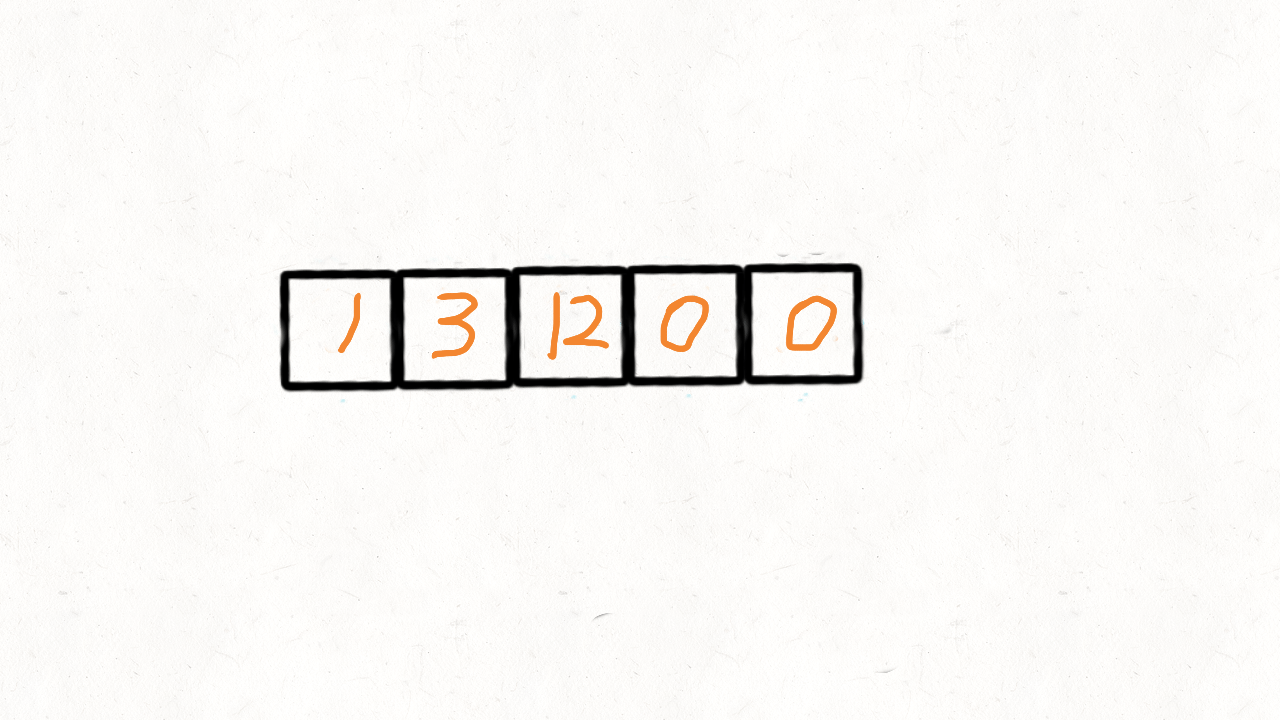
在这里插入图片描述

代码实现2：

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        b, n = 0, len(nums)
        for a in range(n):
            if nums[a] != 0:
                nums[b] = nums[a]
                b += 1
        for i in range(b, n):
            nums[i] = 0

思路3：一次遍历法

这里参考了快速排序的思想，快速排序首先要确定一个待分割的元素做中间点x，然后把所有小于等于x的元素放到x的左边，大于x的元素放到其右边。
这里我们可以用0当做这个中间点，把不等于0(注意题目没说不能有负数)的放到中间点的左边，等于0的放到其右边。
这的中间点就是0本身，所以实现起来比快速排序简单很多，我们使用两个指针i和j，只要nums[i]!=0，我们就交换nums[i]和nums[j]
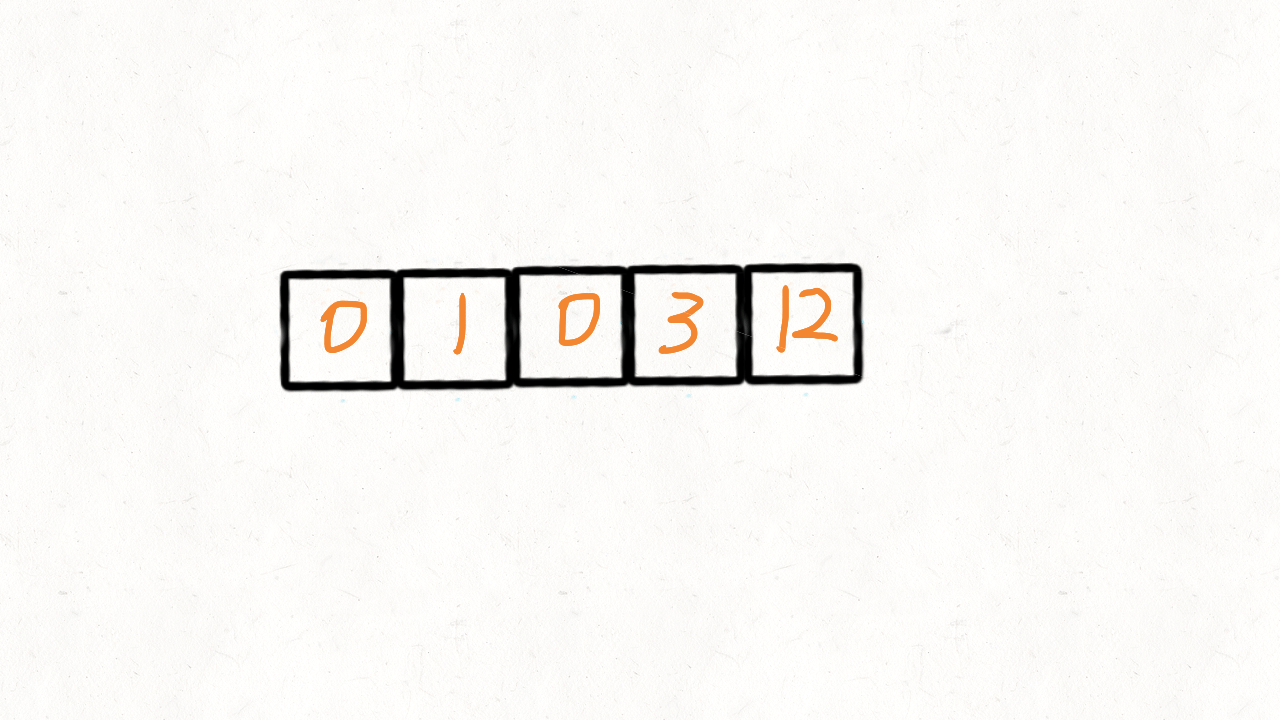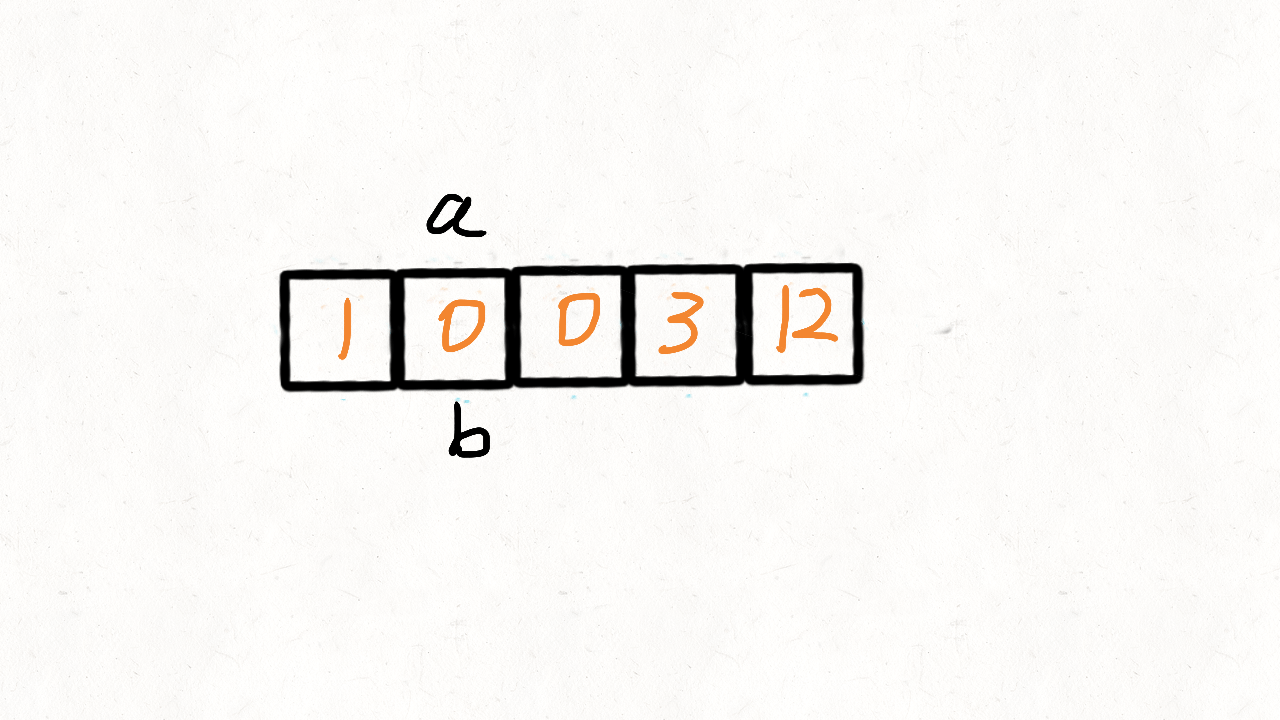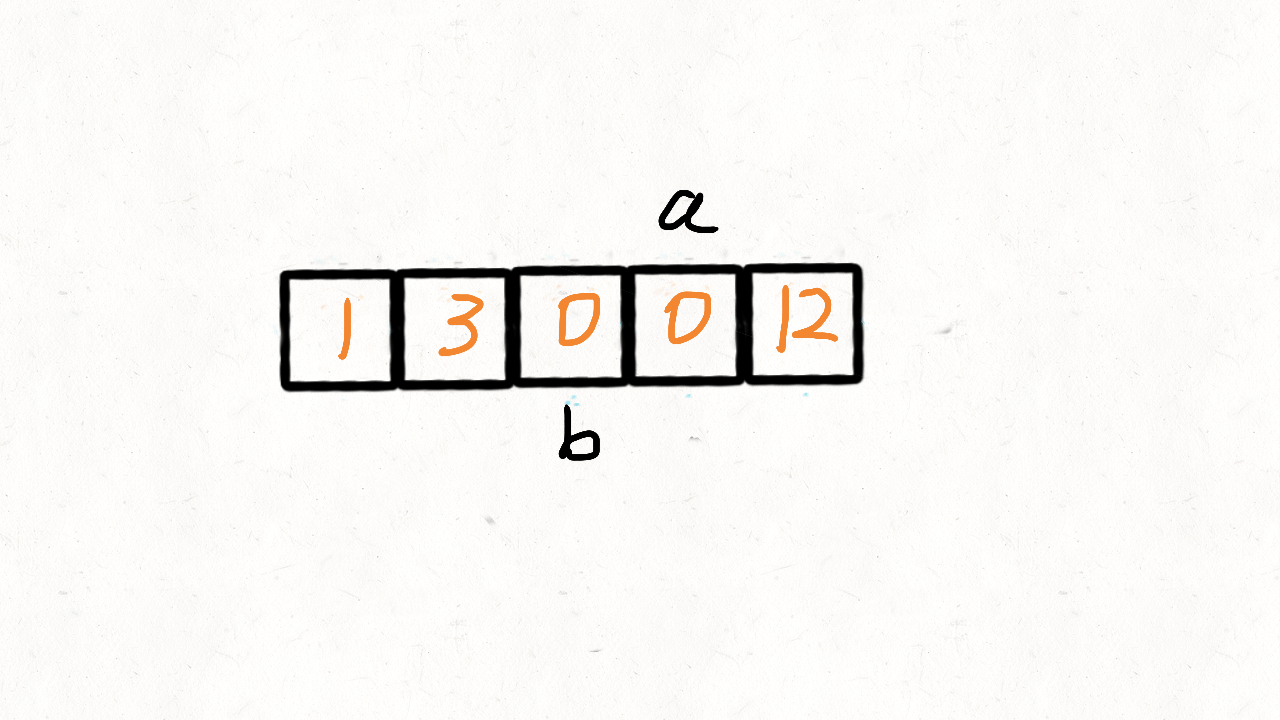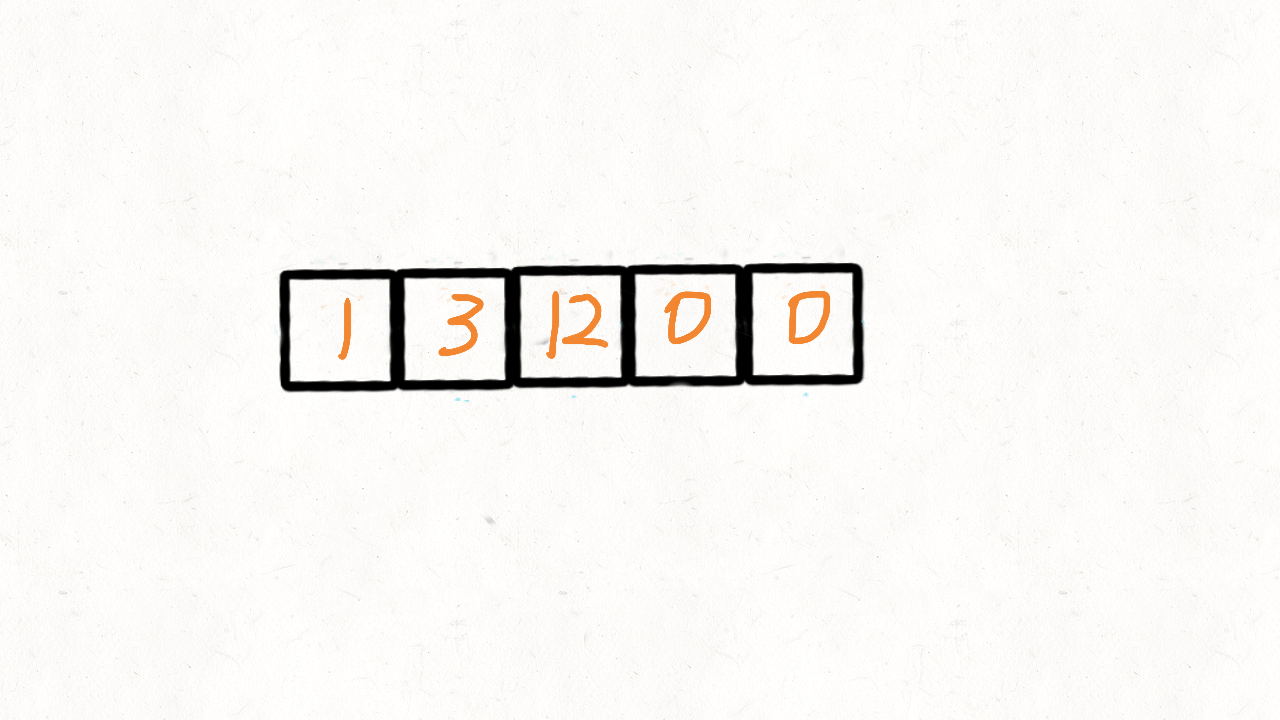
在这里插入图片描述

代码实现3：

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        b = 0
        for a in range(len(nums)):
            if nums[a] != 0:
                nums[b], nums[a] = nums[a], nums[b]
                b += 1

566. 重塑矩阵

在MATLAB中，有一个非常有用的函数 reshape，它可以将一个矩阵重塑为另一个大小不同的新矩阵，但保留其原始数据。
给出一个由二维数组表示的矩阵，以及两个正整数r和c，分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。
如果具有给定参数的reshape操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

示例：

示例 1:
输入: 
nums = 
[[1,2],
 [3,4]]
r = 1, c = 4
输出: 
[[1,2,3,4]]
解释:
行遍历nums的结果是 [1,2,3,4]。新的矩阵是 1 * 4 矩阵, 用之前的元素值一行一行填充新矩阵。

示例 2:
输入: 
nums = 
[[1,2],
 [3,4]]
r = 2, c = 4
输出: 
[[1,2],
 [3,4]]
解释:
没有办法将 2 * 2 矩阵转化为 2 * 4 矩阵。 所以输出原矩阵。

思路：

代码实现：

class Solution:
    def matrixReshape(self, nums: List[List[int]], r: int, c: int) -> List[List[int]]:
    	# 判断重塑是否合理
        num = len(nums) * len(nums[0])
        if num != r * c:
            return nums
        else:
        	# 先将所有元素放入大数组
            matrix = []
            for i in nums:
                matrix.extend(i)
            # 根据行列，从大数组中取值并填入
            reshape = [[matrix.pop(0) for _ in range(c)] for _ in range(r)]
            return reshape

485. 最大连续1的个数

给定一个二进制数组，计算其中最大连续1的个数。

示例：

输入: [1,1,0,1,1,1]
输出: 3
解释: 开头的两位和最后的三位都是连续1，所以最大连续1的个数是 3.

思路1：一次遍历法

使用一个计数器 cur 记录1的数量，另一个计数器 max_len 记录当前最大1的数量
遇到1时：

cur+1

遇到0时

记录当前已经记录的数量，并与最大值比较（放在遇到0时处理，比每次遇到1时就判断要快）
cur设为0

返回 max_len（注意应写为max(max_len, cur)，因为最大值比较放在了遇到0的情况，如果只有遇到1，则max_len的值得不到更新）

代码实现1：

class Solution:
    def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
        max_len = 0
        cur = 0
        for a in range(len(nums)):
            if nums[a] == 1:
                cur += 1
            else:
                max_len = max(max_len, cur)
                cur = 0
        return max(max_len, cur)

思路2：使用map

使用 map 和 join 来解决此问题。
使用 splits 函数在 0 处分割将数组转换成字符串。
在获取子串的最大长度就是最大连续 1 的长度。

代码实现2：

class Solution:
    def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
        # 将整数组成的列表转为一个长字符串
        str1 = ''.join(map(str, nums))
        # 对字符串按照0切割，返回的列表中只有每个元素只有1组成
        str2 = str1.split('0')
        # 统计每个元素的长度并取最大值
        max_len = max(map(len, str2))
        return max_len