数组/列表 1. 两数之和 15. 三数之和 169. 多数元素

1. 两数之和

• 给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。
  你可以假设每种输入只会对应一个答案。但是，你不能重复利用这个数组中同样的元素。

示例：

给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

思路：

遍历一次数组，将数组的值及其索引放入哈希表。
遍历第二次数组，利用b = target - a 的关系寻找b是否存在与哈希表，若存在，且索引与a不同，则返回。

代码实现：

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        hash_map = {}

        for i, n in enumerate(nums):
            hash_map[n] = i

        for j, m in enumerate(nums):
            n = target - m
            i = hash_map.get(n)
            if n in hash_map and j != i:
                return [j, i]

15. 三数之和

• 给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。
  注意：答案中不可以包含重复的三元组。

示例：

给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]

思路：

这道题的难点是不能包含重复的答案，对于[0,0,0,0,0]这个数组，答案只有一个[0,0,0]。
首先我们对数组先排序一次，在排好序的数组上，就很容判断前后元素是否相当，这样可以过滤掉重复的答案。
再定义三个指针，k，i，j如下图所示

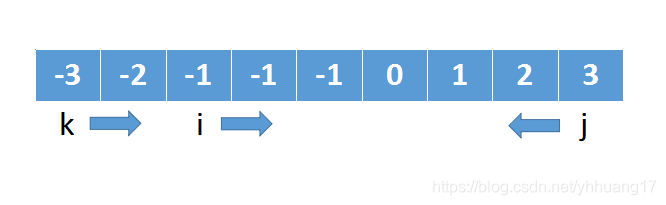
指针i从左往右移动，且始终比k大一位，这样就保证不会跟k重叠，
指针j从右往左移动，且始终比i大，这样i和j就不会重叠，即三个指针都不会重叠。
在这个基础上，实现我们的主要逻辑：

nums[k]>0时，可以直接跳出循环，因为nums[k]都比0大了，后面的nums[i]和nums[j]肯定更大，三者加起来肯定大于0
nums[k]和nums[k-1]相等，即前后元素重复了，需要过滤掉
如果nums[i]+nums[j]+nums[k]>0，即三者之和太大了，我们将j指针左移，因为三个数中最大的肯定是nums[j]，将j左移就可以减小三者之和。
如果nums[i]+nums[j]+nums[k]<0，说明三者之和太小了，同理将i指针右移
如果nums[i]+nums[j]+nums[k]==0，这就是要找的答案，将其保存起来，同时i右移，j左移
i和j在移动的过程中还需要判断前后元素是否重复

代码实现：

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return []
        # 正式处理之前，先将数组排序
        nums = sorted(nums)
        n = len(nums)
        res = []
        # 假设数组为[0,1,2,3,4,5,6,7,8,9,10]
        # 第三个指针k最多到下标8位置，因为后面两个位置需要留给另外两个指针
        for k in range(n - 2):
            # nums[k]>0，说明后面的元素肯定也大于0，最后结果肯定>0，故直接跳出
            if nums[k] > 0:
                break
            # 如果当前元素和前面一个元素一样，忽略重复元素
            if k > 0 and nums[k - 1] == nums[k]:
                continue
            # 定义另外两个指针 i 和 j
            i, j = k + 1, n - 1
            while i < j:
                tmp = nums[i] + nums[j] + nums[k]
                # 如果三数之和>0，说明最右边的值太大了，
                if tmp > 0:
                    j -= 1
                    # j向左移动之后，当前元素和移动前元素相同，则继续向左移
                    while i < j and nums[j + 1] == nums[j]:
                        j -= 1
                # 如果三数之和<0，说明左边的值太小了
                elif tmp < 0:
                    i += 1
                    # i向右移动之后，当前元素和移动前元素相同，则继续向右移
                    while i < j and nums[i - 1] == nums[i]:
                        i += 1
                # 三数之和等于0，保存结果
                # 同时左指针往右移动，右指针往左移动，
                # 如果移动过程中碰到重复元素，则继续移动
                else:
                    res.append([nums[k], nums[i], nums[j]])
                    i += 1
                    j -= 1
                    while i < j and nums[i - 1] == nums[i]:
                        i += 1
                    while i < j and nums[j + 1] == nums[j]:
                        j -= 1
        return res

169. 多数元素

• 给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
  你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例：

示例 1:
输入: [3,2,3]
输出: 3

示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2

思路1：排序

如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序，那么下标为 $\frac{n}{2}$ 的元素（下标从 0 开始）一定是众数。

代码实现1：

class Solution:
    def majorityElement(self, nums):
        nums.sort()
        return nums[len(nums)//2]

思路2：哈希表

我们知道出现次数最多的元素大于 $\frac{n}{2}$ 次，所以可以用哈希表来快速统计每个元素出现的次数。

代码实现2：

class Solution:
    def majorityElement(self, nums):
        hash_map = {}
        for i in nums:
            if i not in hash_map:
                hash_map[i] = 1
            else:
                hash_map[i] += 1
            if hash_map.get(i) > len(nums) // 2:
                return i