一、神经网络概述
神经网络,简称NN,我们可以将一个最简单的神经网络表示如下图所示:

1、A部分是把样本 ,通过如下的线性处理
,通过如下的线性处理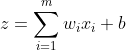
2、再通过B部分一个激活函数,进行数据处理得到输出结果
我们将神经网络分为三层,一个输入层(inputs layer)
一个输出层(output layer)
中间加入多层的隐藏层(hidden layer),以增加模型的泛化能力,如下图所示:

二、前向传播
将所有输入和神经元和神经元之间组成一个全连接网络,如下图所示,

图示说明:
1、黑色的标注,我们认为是第一层,红色标注,我们认为是第二层,等会会在上标上加以区别
2、 表示输入
表示输入
3、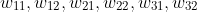 表示线性参数,若在第一层,加上上标
表示线性参数,若在第一层,加上上标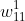 ,矩阵用W
,矩阵用W
4、 表示偏置值,若在第一层,加上上标
表示偏置值,若在第一层,加上上标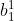
5、 表示一层的输出值,若在第一层,加上上标
表示一层的输出值,若在第一层,加上上标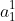
6、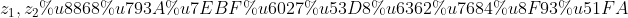 表示线性变换的输出,若在第一层,加上上标
表示线性变换的输出,若在第一层,加上上标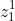
7、每层的神经元,会通过激活函数 (A),进行非线性变换
(A),进行非线性变换
则有如下公式:

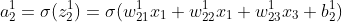
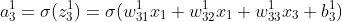
则每一层则归纳为如下:
第一层: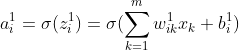
后续层: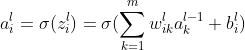
三、关于激活函数 ()
()
是对输出进行一次非线性变化,在感知机中用的是sign(z),简单,但是处理能力有限,在神经网络中,引入了其他激活函数,比如有Sigmoid函数,还有tanx,softmax,ReLU函数等,每个函数对输出值进行进一步的改进。
(个人觉得是,线性函数对数据的划分能力非常有限,引入了Sigmoid等函数,加强了对模型的泛化能力!)
在前向传播中,参数w和b的值都是初始的某个数,我们需要通过后续介绍的反向传播对参数进行更新。








 本文介绍了神经网络的基础知识,包括神经网络的结构和前向传播过程。首先,概述了神经网络由输入层、隐藏层和输出层组成,并解释了激活函数在模型中的作用。接着,详细阐述了前向传播的过程,描述了如何通过线性变换和非线性激活函数计算神经元的输出。最后,讨论了不同的激活函数,如Sigmoid、ReLU等,及其对模型泛化能力的影响。
本文介绍了神经网络的基础知识,包括神经网络的结构和前向传播过程。首先,概述了神经网络由输入层、隐藏层和输出层组成,并解释了激活函数在模型中的作用。接着,详细阐述了前向传播的过程,描述了如何通过线性变换和非线性激活函数计算神经元的输出。最后,讨论了不同的激活函数,如Sigmoid、ReLU等,及其对模型泛化能力的影响。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








