概述
已知样本空间如何快速查询得到其近邻?唯有以空间换时间,建立索引是最基本的解决方式。但是索引建立的方式各有不同,kd树只是是其中一种。它的思想如同分治法,即:利用已有数据对k维空间进行切分。
注意:在一维空间里面,二叉查找树就是KD树的情形。

对于一颗二叉查找树,可以在空间上理解:树的每个节点把对应父节点切成的空间再切分,从而形成各个不同的子空间。查找某点的所在位置时,就变成了查找点所在子空间。二叉查找树仅仅是一维,如果换到二维?
如下图, 这样可以将平面分为两个部分。
如下图, 这样可以将平面分为四个部分。
如下图, 这样可以将平面分为8个部分。

1.节点深度时是偶数值,再细分,利用X坐标(垂直的线)
2.节点深度时是奇数值,然后细分,使用Y坐标(水平线)
例子

伪代码

KDTree构建
KDTree::KDNode* KDTree::constructKDTree(std::list<Vector2f>& _data, uint32_t _depth)
{
auto size = _data.size();
if (size == 1)
return new KDNode(_data.front());
//深度是偶数
if (_depth % 2 == 0)
_data.sort([](Vector2f a, Vector2f b)
{
return a[X] < b[X];
});
//深度是奇数
else
{
_data.sort([](Vector2f a, Vector2f b)
{
return a[Y] < b[Y];
});
}
auto mid = size / 2;
auto mid_ptr = _data.begin();
std::advance(mid_ptr, mid);//找到中点的迭代器
auto left_list = std::list<Vector2f>(_data.begin(), mid_ptr);//划分左子集
auto right_list = std::list<Vector2f>(mid_ptr, _data.end());//划分左子集
auto left_child = constructKDTree(left_list,_depth+1);
auto right_child = constructKDTree(right_list, _depth + 1);
//_depth % 2 表示X还是Y
return new KDNode((*mid_ptr)[_depth % 2], left_child, right_child);
}
void KDTree::preprocessBoundaries(KDNode* _node, bool _isEventDepth)
{
if (!_node || isALeaf(_node))
return;
//非叶子节点就是左右分界线,这个界限值
if (_isEventDepth)//偶数深度->对x划分
{
if (_node->left)
{
_node->left->boundary = _node->boundary;//先初始化原先的边界
_node->left->boundary.x_max = _node->value;
preprocessBoundaries(_node->left, !_isEventDepth);
}
if (_node->right)
{
_node->right->boundary = _node->boundary;//先初始化原先的边界
_node->right->boundary.x_min = _node->value;
preprocessBoundaries(_node->right, !_isEventDepth);
}
}
else
{
if (_node->left)
{
_node->left->boundary = _node->boundary;//先初始化原先的边界
_node->left->boundary.y_max = _node->value;
preprocessBoundaries(_node->left, !_isEventDepth);
}
if (_node->right)
{
_node->right->boundary = _node->boundary;//先初始化原先的边界
_node->right->boundary.y_min = _node->value;
preprocessBoundaries(_node->right, !_isEventDepth);
}
}
}
KDTree(std::list<Vector2f> _data)
{
root = constructKDTree(_data, 0);
//叶子节点是具体的数据,像B+树一样
//非叶子节点储存的是边界线的值,偶数层是按照x分割,奇数层是按照y分割
root->boundary = default_bound;
preprocessBoundaries(root, true);//构造每个非叶子节点的区域边界
}
2D搜寻
例子
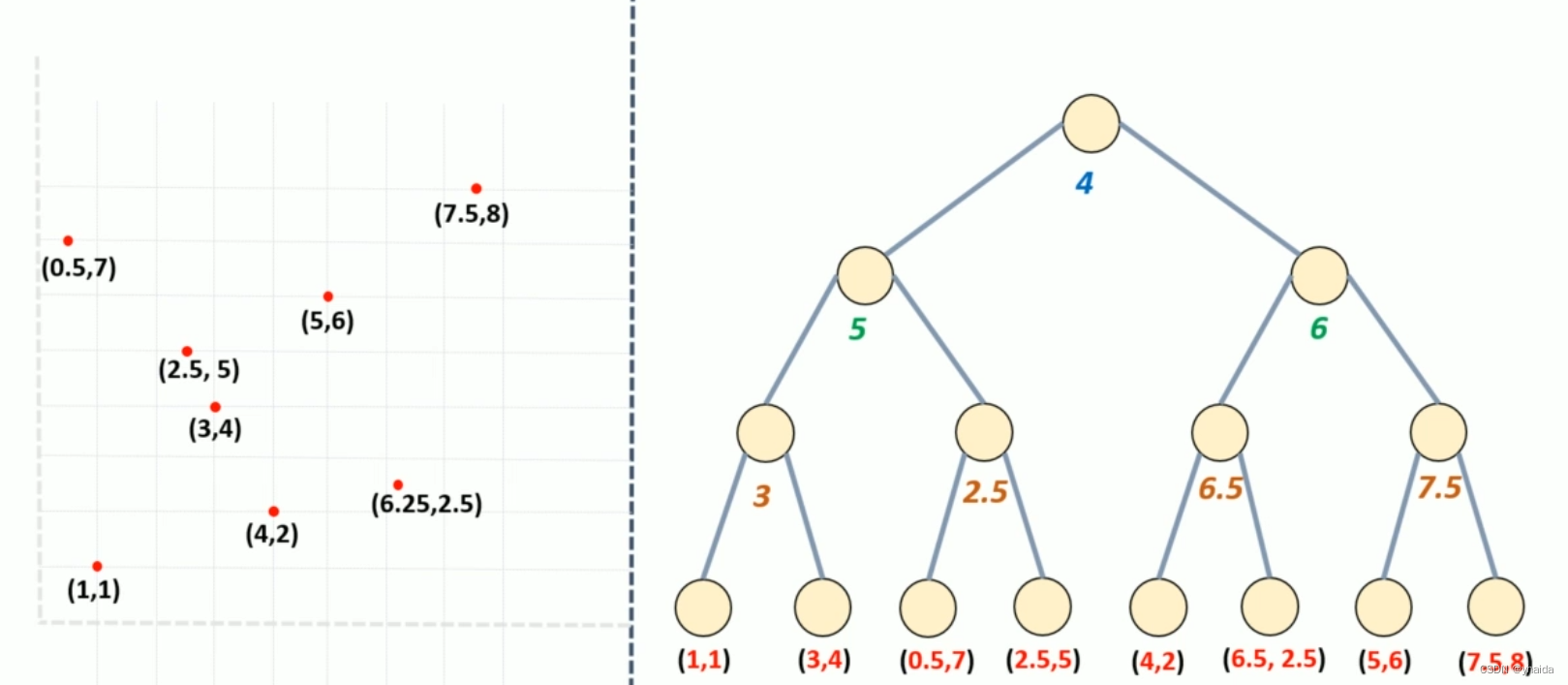
根据颜色依次搜寻

伪代码

boolKDTree::isInside(const KDRange& r1, const KDRange& r2)
{
if (r1.x_min >= r2.x_min &&
r1.x_max <= r2.x_max &&
r1.y_min >= r2.y_min &&
r1.y_max <= r2.y_max)
return true;
return false;
}
bool KDTree::isIntersect(const KDRange& r1, const KDRange& r2)
{
if (r1.x_max < r2.x_min &&
r1.x_min > r2.x_max)
return false;
if (r1.y_max < r2.y_min &&
r1.y_min > r2.y_max)
return false;
return true;
}
bool KDTree::isInRange(const Vector2f& p, const KDRange& r)
{
if (p[X] >= r.x_min && p[X] <= r.x_max &&
p[Y] >= r.y_min && p[Y] <= r.y_max)
return true;
return false;
}
void KDTree::searchKDTree(KDNode*_node, KDRange _range, std::list<Vector2f>&_list)
{
if (isALeaf(_node))
{
if (isInRange(_node->data, _range))
_list.push_back(_node->data);
}
else//两边都得判断是因为如果_node处于_range之间
{
//左边界
if (isInside(_node->left->boundary, _range))
{
traverse(_node->left, _list);
}
else if(isIntersect(_node->left->boundary,_range))
{
searchKDTree(_node->left, _range, _list);
}
//有右边界
if (isInside(_node->right->boundary, _range))
{
traverse(_node->right, _list);
}
else if (isIntersect(_node->right->boundary, _range))
{
searchKDTree(_node->right, _range, _list);
}
}
}
KNN邻近搜寻
顾名思义,最近邻搜索是指接近性在给定集合中寻找最接近(或最相似的)到一个给定的点。

特殊情况,找到点4,2但是实际点是3,4

伪代码

void KDTree::nearestNeighbour(KDNode* _node, const Vector2f& _value, float& _current_distance, bool _even_depth, Vector2f& _current_nn)
{
//如果是叶子节点那么就要计算距离并更新
if (isALeaf(_node))
{
auto distance = sqrd_distance(_value, _node->data);
if (distance < _current_distance)
{
_current_distance = distance;
_current_nn = _node->data;
return;
}
}
else
{
auto index = _even_depth ? X : Y;
if (_value[index] < _node->value)
{
nearestNeighbour(_node->left, _value, _current_distance, !_even_depth, _current_nn);
if(fabs(_value[index]-_node->value)<_current_distance)//关键,如果距离另一边更近则继续搜寻
nearestNeighbour(_node->right, _value, _current_distance, !_even_depth, _current_nn);
}
else
{
nearestNeighbour(_node->right, _value, _current_distance, !_even_depth, _current_nn);
if (fabs(_value[index] - _node->value) < _current_distance)//关键,如果距离另一边更近则继续搜寻
nearestNeighbour(_node->left , _value, _current_distance, !_even_depth, _current_nn);
}
}
}

























 820
820

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










