最小生成树——Prim算法和Kruskal算法

最小生成树——Prim算法和Kruskal算法

一、prim算法解析

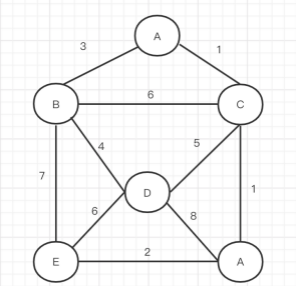
以上图为例。

prim算法从任意顶点开始，每次都找到一个距离顶点集中距离最近的一个点，将其加入到顶点集，并把两点间的边加入到树中。直到访问完所有点，得到的就是最小生成树。
步骤：
1、从点A开始，将其加入到顶点集中，此时涉及的边有两条，[A,B]和[A, C],显然可以判断出后者距离更小，所以把C点加入到顶点集中。

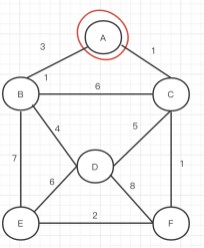
2、在此顶点集中，涉及的边数增加，在所有边中继续寻找顶点集中没有的距离最短的点。这里可以找到第三个点为F。以此类推，可以访问到所有点。
注意：
1、不可以构成回路。
2、遇到权值相同的任选一个点，对结果没影响。

二、Kruskal算法
上面的prim算法是从点的角度下手，而Kruskal算法是从边下手。

以上图为例

步骤：
1、首先将边按小到大的顺序排序。实例中排序可得，(1, 4), (2, 3),(0, 1), (1, 4),(1, 2),(2, 4),(3, 4)。
2、从小到大取出边及连接边的起始点和终止点，将取出的点和边做记号放入同一个集合中。直 到所有的点存入同一个集合并没有形成回路。如下图演示：




注意：其中当选取到边<1, 4>时，因为0， 1， 4已经在同一集合中，选取边<1, 4>后会造成回路，所以直接到下一条边<1, 2>。

三、完整代码

#include<iostream>
using namespace std;


//prim算法
#define X 10000
const int N = 6;
int edge[N] = {0};
bool visit[N];
int graph[N][N] = { { X, 3, 1, X, X, X},  //INF代表两点之间不可达
                    { 3, X, 6, 4, 7, X},
                    { 1, 6, X, 5, X, 1},
                    { X, 4, 5, X, 6, 8},
                    { X, 7, X, 6, X, 2},
                    { X, X, 1, 8, 2, X}
                  };

int prim(int spot){

    int index = spot;
    int i = 0;
    int j = 0;
    int sum = 0;
    memset(visit,false, sizeof(visit));
    visit[spot] = true;

    cout << "最小生成树: ";
    cout << index << " ";
    for(i = 0; i < N; i++){
        edge[i] = graph[index][i];
    }
    for(i = 1; i < N; i++){

        int value = X;

        for(j = 0; j < N; j++){//找到未访问过的最小权值的点
            if(!visit[j] && edge[j] < value){
                value = edge[j];
                index = j;
            }
        }

        visit[index] = true;//标记刚刚找到的点
        cout << index << " ";
        sum += edge[index];// 累加权值

        for(j = 0; j < N; j++){//更新数组edge的值
            if(!visit[j] && edge[j] > graph[index][j]){
                edge[j] = graph[index][j];
            }
        }
    }

    cout << endl;
    cout << "最短距离: ";
    return sum;
}


//kruskal算法
#define N 7
typedef struct node{
    int val;//权值
    int start;//起始点
    int end;//终止点
}Node;
Node V[N];

int Edge[N][3] = {  { 0, 4, 1},
                    { 2, 3, 2},
                    { 0, 1, 4},
                    { 1, 4, 4},
                    { 1, 2, 5},
                    { 2, 4, 6},
                    { 3, 4, 7}
                    };
 
int father[N] = {0};
int cap[N] = {0};
 
void make_set()              //初始化集合，让所有的点都各成一个集合，每个集合都只包含自己
{
    for(int i = 0; i < N; i++)
    {
        father[i] = i;//各成一个集合
        cap[i] = 1;//集合中结点个数
    }
}
 
int find_set(int x)              //找出点属于哪个集合
{
    if(x != father[x])
     {
        father[x] = find_set(father[x]);//运用递归找出点的“祖集合”
    }
    return father[x];
}
 
void Union(int x, int y)         //将x,y两点合并到同一个集合
{
    x = find_set(x);
    y = find_set(y);
    if(x == y)
        return;
    if(cap[x] < cap[y])
        father[x] = find_set(y);
    else
    {
        cap[x] += cap[y];
        father[y] = find_set(x);
    }
}
 
int Kruskal()
{
    int sum = 0;
    make_set();//初始化集合
    for(int i = 0; i < N; i++)//将边从小到大排序后，依次取出
    {
        if(find_set(V[i].start) != find_set(V[i].end))     //如果改变的两个顶点还不在一个集合中，就并到一个集合里，生成树的长度加上这条边的长度
        {
            Union(V[i].start, V[i].end);  //合并两个顶点到一个集合
            sum += V[i].val;
        }
    }
    return sum;
}
int main(){
    cout << "prim算法结果: " << endl;
    cout << prim(0) << endl;
    
    cout << "Kruskal算法结果: " << endl;
    for(int i = 0; i < N; i++)   //初始化边的数据
    {
        V[i].start = Edge[i][0];
        V[i].end = Edge[i][1];
        V[i].val = Edge[i][2];
    }
    cout << "最小生成树权值: ";
    cout << Kruskal()<< endl;
    return 0;
}