快速傅里叶变换python实现

一、前言

　　我想认真写好快速傅里叶变换(Fast Fourier Transform，FFT)，所以这篇文章会由浅到细，由窄到宽的讲解，但是傅里叶变换对于寻常人并不是很容易理解的，所以对于基础不牢的人我会通过前言普及一下相关知识。

　　我们复习一下三角函数的标准式：$$y=A\cos (\omega x+\theta )+k$$

　　\(A\)代表振幅，函数周期是\(\frac{2\pi}{w}\)，频率是周期的倒数\(\frac{w}{2\pi}\)，\(\theta\)是函数初相位，\(k\)在信号处理中称为直流分量。这个信号在频域就是一条竖线。

　　我们再来假设有一个比较复杂的时域函数\(y=f(t)\)，根据傅里叶的理论，任何一个周期函数可以被分解为一系列振幅\(A\)，频率\(\omega\)
或初相位\(\theta\)正弦函数的叠加

\[y = A_1sin(\omega_1t+\theta_1) +  A_2sin(\omega_2t+\theta_2) +  A_3sin(\omega_3t+\theta_3) \]

　　该信号在频域有三条竖线组成，而竖线图我们把它称为频谱图，大家可以通过下面的动画了解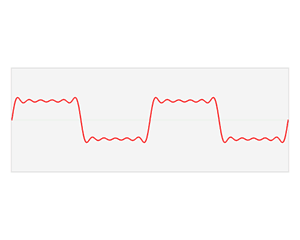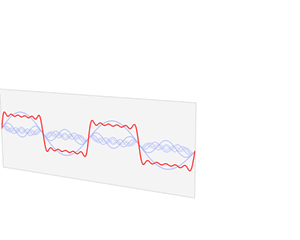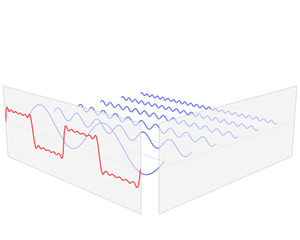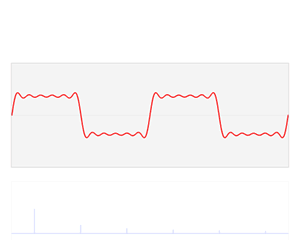

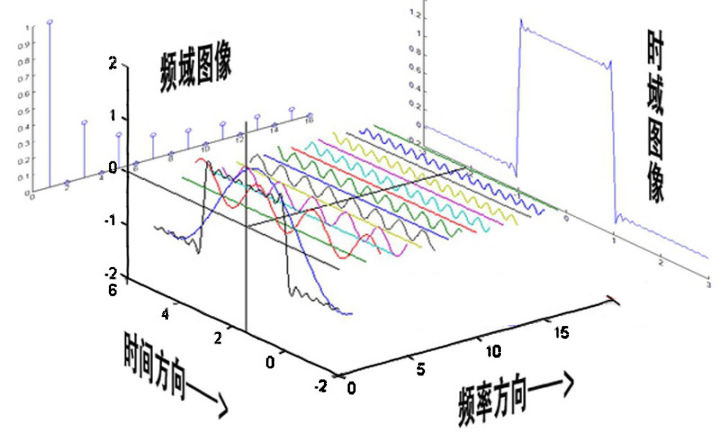
　如图可知，通过时域到频域的变换，我们得到了一个从侧面看的频谱，但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每个正弦波对应频率的振幅是多少，而没有提到相位。基础的正弦波\(Asin(wt+\theta )\)中，振幅，频率，相位缺一不可，不同相位决定了波的位置，所以对于频域分析，仅仅有频谱(振幅谱)是不够的，我们还需要一个相位谱。

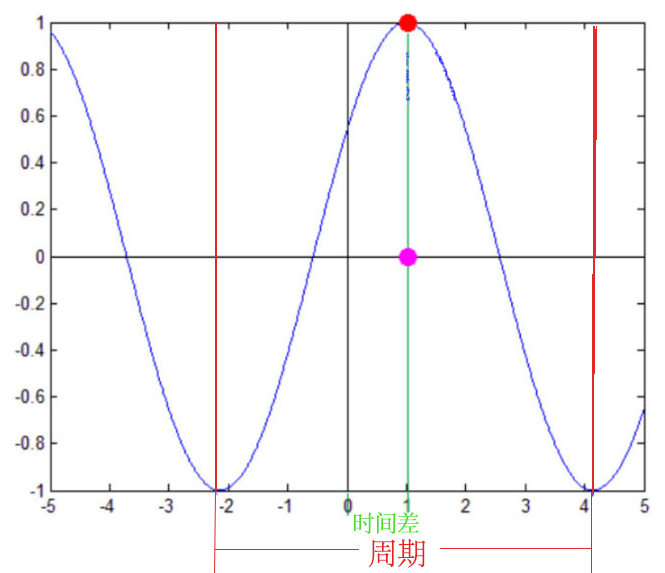
　　我依稀记得高中学正弦函数的是时候，\(\theta\)的多少决定了正弦波向右移动多少。当然那个时候横坐标是相位角度，而时域信号的横坐标是时间，因此我们只需要将时间转换为相位角度就得到了初相位。相位差则是时间差在一个周期中所占的比例

\[\theta=2\pi \frac{t}{T} \]

所以傅里叶变换可以把一个比较复杂的函数转换为多个简单函数的叠加，将时域(即时间域)上的信号转变为频域(即频率域)上的信号，看问题的角度也从时间域转到了频率域，因此在时域中某些不好处理的地方，在频域就可以较为简单的处理，这就可以大量减少处理信号计算量。\(\color{FF0000}{信号经过傅里叶变换后，可以得到频域的幅度谱以及相位谱，信号的幅度谱和相位谱是信号傅里叶变换后频谱的两个属性}\)

傅里叶用途

• 时域复杂的函数，在频域就是几条竖线
• 求解微分方程，傅里叶变换则可以让微分和积分在频域中变为乘法和除法

傅里叶变换相关函数

　　假设我们的输入信号的函数是

\[S=0.2+0.7*\cos (2\pi*50t