博主分享了在一场编程竞赛中的经历，涉及Dijkstra算法、DFS优化、TSP问题、最小生成树算法（Prim和Kruskal），以及对题目的理解误区和策略调整。最后反思了110分的失分教训。
7:50−8:307:50-8:307:50−8:30
看题
8:30−9:008:30-9:008:30−9:00
写出来 T4T4T4 的迪杰斯特拉，每次枚举删掉一条边，然后跑一遍。应该有 404040 分？
9:00−9:409:00-9:409:00−9:40
因为觉得枚举每一条边会有很多冗余的复杂度，所以瞎搞出来了个 dfs 来判断哪些边对从 111 节点到 nnn 节点的最短路有贡献，把这些边存下来，只枚举删掉这些边的话结果会怎样。运气好点的话可能 606060。
9:40−10:309:40-10:309:40−10:30
做 T2T2T2 ，一开始没看清题上给的条件 Cost[A,B]=min∣xA−xB∣,∣yA−yB∣,∣zA−zB∣Cost[A,B] = min{ |xA-xB|, |yA-yB|, |zA-zB| }Cost[A,B]=min∣xA−xB∣,∣yA−yB∣,∣zA−zB∣，肥肠难过，用空间中两点距离公式搞了搞，还在纸上手推连边时能不能贪心优化。
注意到之后发现贴脸 最小生成树 应该可以拿到一些分，但是没有想到在连边时如何优化，所以得连成一个完全图，这样的话首先想到的是Prim算法，算了下空间可能要 400+MB400+MB400+MB，提面上没直接说空间，我就看 ojojoj 上写的是 256MB256MB256MB，所以敲了个克鲁斯卡尔。
等敲完的时候看下发文件中给的文件名时才注意到上面说 内存512M时限均为1s内存512M 时限均为1s内存512M时限均为1s ，一道题有俩地方都没注意到，不知道还能不能水 606060 分。然后就想要不算下时间复杂度，卡着时间复杂度只连一些比较近的边，然后再最小生成树。
但是怕不稳，没写。
10:30−11:1010:30-11:1010:30−11:10
T3T3T3 直接分层图，能过两个样例。
11:10−结束11:10-结束11:10−结束
搞 T1T1T1 ，用二进制枚举状态的话能 303030 分，先把所有球的起点 sort 一遍后的相当于只改变了每个球的下标而不影响后边的操作，这样球i的位置永远不可能到j的右边 (i<j)(i < j)(i<j)，然后就方便判断碰撞了。
然后只要中规中矩模拟就可以水到分。
但是我在一些点上卡死了，肥肠难过，我以为
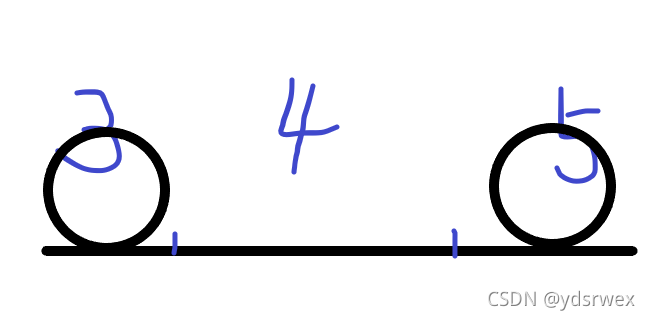
这种时候两球会在 444 碰撞一下然后再回到 333 和 555 上。
而且直接模拟的时候，一群球撞到一起很难处理。
T1T1T1 看错题意了，球是无体积的，如果基于这一性质，再往下稍微一推就很容易知道球和球相撞的话只不过相当于没有接触过，即相互穿了过去，这样的话 505050 分就很可得了，再稍微用头想一下就应该能想到每个球最终的结果只有两种，看是否匹配得上就行，然后就可以往正解方向上想了。
T2T2T2 没有用贪心优化一下，每个点最多只会连 666 个点，即x，y，zx，y，zx，y，z 分别最接近的时候，这样的话也不需要什么 PrimPrimPrim 了，用三个不一样的 sort 排下序，然后每次排完来连一波边。而且数组还开小了，往后面再加俩 000 就又多 101010 分。亏我考试的时候还想要不找最接近的几十个连下边得了，要不然也能 AAA 掉了。（把所谓 正解 当成暴力了）
T3T3T3 直接 AAA
T4T4T4 想简单了，没想到还有种那么损的可能，就是小 AAA 快到终点的时候你再把路拆掉，让他只能返回好远的路，然后重新跑最短路。不过还好想简单了，忽略掉这一情况水到的分比直接输出 −1-1−1 要多。
失误挂了 110110110 分，肥肠难受。
扫一扫
708
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
