普通最小二乘法的推导证明

Ref: https://my.oschina.net/keyven/blog/526010

前言

        普通最小二乘法（ordinary least squares, OLS）是线性回归预测问题中一个很重要的概念，在 Introductory Econometrics A Modern Approach (Fourth Edition) 第2章 简单回归模型 中，花了很详细的篇幅对此作出介绍。应聘数据挖掘岗位，就有考到对普通最小二乘法的推导证明。最小二乘法十分有用，例如可以用来做推荐系统、资金流动预测等。

推导证明

(1) 公式推导

(2) 求和性质

        求和性质，具体可以参考Introductory Econometrics A Modern Approach (Fourth Edition) 一书（计量经济学导论，第4版，杰弗里·M·伍德里奇 著）的附录A。

(3) 一般形式

        有了上述推导证明，普通最小二乘法一般形式可以写成（字母盖小帽表示估计值，具体参考应用概率统计）：

重要概念

        接下来简单地介绍几个重要概念，并在下一章节给出最小二乘法的无偏估计。

        记第i 次观测残差（residual）是yi 的实际值与其拟合值之差：

        

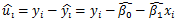
        其中SST=SSE+SSR。

        拟合优度，有时又称“判定系数”，回归的R2（R-squared），用来判断直线拟合效果：

        当R2 = 1时称为完美拟合，当R2 = 1时称为糟糕拟合，最理想的观测是，第i 次情况 残差u=0。

        事实上，R2不因y 或x 的单位变化而变化。

        零条件均值，指给定解释变量的任何值，误差的期望值为零。换言之，即 E(u|x)=0。

无偏估计

        我们追求零条件均值，得到OLS 估计量的无偏估计：

        其中，

        现在我们可以看到，β1 的估计量等于总体斜率β1 加上误差 { u1, u2, ..., un }的一个线性组合。

“线性”含义

        线性回归问题中，“线性”的含义是指被估计参数β1 和β2 是线性相关的，而不关心解释变量与被解释变量以何种形式出现，例如y = kx + b，log(y) = kx + b，log(y) = klog(x) + b，etc. 下面列举一些常用的曲线方程：

1、双曲线 1/y = a + b/x

令y'=1/y，x'=1/x，则有y'=a+bx'

2、幂函数曲线y=axb

令y'=lny，x'=lnx，a'=lna，则有y'=a'  +bx'

3、指数函数曲线y=aebx

令y'=lny，x'=x，a'=a，则有y'=a'+b  x'

4、负指数函数曲线y=aeb/x（同上）

5、对数函数y=a+blnx

令y'=y，x'=lnx，则有y'=a+bx'

6、S型（Logistic，逻辑斯蒂回归）曲线y=K/(1+Ae-λx)

令y'=ln((K-y)/y)，a=lnA，则有y'=a-λx

多重线性回归

        多重回归研究的是变量y 与可控变量x1，x2，...，xk 之间的线性关系，假设

        根据线性代数，则有

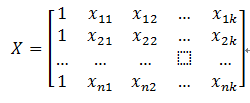
        得到

        与普通最小二乘法推导证明相似，可以得到β 的最小二乘估计

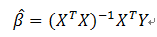
        此处不作证明，具体可参考《应用概率统计 张国权 著》第九章 回归分析。