二叉树---1

最新推荐文章于 2022-12-28 22:23:33 发布

yanyang已存在！

最新推荐文章于 2022-12-28 22:23:33 发布

阅读量249

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构

本文链接：https://blog.youkuaiyun.com/yanyang42/article/details/80945181

数据结构专栏收录该内容

5 篇文章

订阅专栏

本文详细介绍了二叉树的概念、性质及存储方式，并深入探讨了遍历方法及其应用，包括先序、中序、后序及层次遍历。此外，还介绍了如何通过不同方式构建二叉树。

一、二叉树

二叉树（Binary Tree）是n（n>=0）个结点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根结点和两颗互不相交的，分别称为根结点的左子树和右子树的二叉树；

二、二叉树的性质

（1）性质1：在二叉树的第i层上至多有个结点

（2）性质2：深度为k的二叉树至多有个结点（k≥1）

（3）性质3：对任何一颗二叉树T，如果其终端结点数为n0,度为2的结点数为n2，则no=n2+1;

（4）性质4：具有n个结点的完全二叉树的深度为，（[ ]表示不大于x的最大整数）

（5）性质5：如果对一颗有n个结点的完全二叉树）（其深度为）的结点按层序编号（从第1层到第层，每层从左到右），对任一结点i(1≤i≤n)有：

1.如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是结点[i/2];

2.如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i;

3.如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1.

三、二叉树的的存储结构

1、二叉树的顺序存储结构：用一维数组存储二叉树中的结点，并且结点的存储位置，也就是数组的下标要能体现结点之间的逻辑关系，比如双亲与孩子的关系。

下标：

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

So :顺序结构一般适合用于完全二叉树，才不会造成存储空间的浪费

2、二叉链表结构：由于顺序存储适用性不强，所以提出链式存储结构。二叉树每个结点最多有2个孩子，所以设计如下的结构：

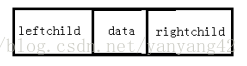
所以二叉树链表的结点结构定义为：

typedef char ElemType;  
#define END '#'

typedef struct BtNode   //二叉树定义结点
{
	ElemType data;
	BtNode* leftchild;
	BtNode* rightchild;
}BtNode,*BinaryTree;

3、遍历二叉树：从根结点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次；

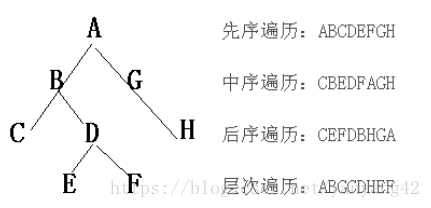
（1）先序遍历：先访问根结点，然后前序左子树，再前序右子树；

void PreOrder(BtNode* p)  //先序遍历
{
	if (p!=NULL)
	{
		cout << " " << p->data;
		PreOrder(p->leftchild);
		PreOrder(p->rightchild);
	}	
}

（2）中序遍历：从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后访问根结点，最后中序遍历右子树；

void InOrder(BtNode* p)//中序遍历
{
	if (p!= NULL)
	{
		InOrder(p->leftchild);
		cout << " " << p->data;
		InOrder(p->rightchild);
	}	
}

（3）后序遍历：从左到右先叶子后结点的方式访问左右子树，最后访问根结点；

void PastOrder(BtNode* p)//后序遍历
{
	if (p != NULL)
	{
		PastOrder(p->leftchild);
		PastOrder(p->rightchild);
		cout << " " << p->data;
	}	
}

（4）层次遍历：从根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问；

void LevelOrder(BtNode* ptr)//层次遍历
{
	if (ptr==NULL)
	{
		return;
	}
	queue<BtNode*> d1;
	d1.push(ptr);
	while (!d1.empty())
	{
		ptr = d1.front();
		cout << ptr->data << " ";
		d1.pop();
		if (ptr->leftchild)
		{
			d1.push(ptr->leftchild);
		}
		if (ptr->rightchild)
		{
			d1.push(ptr->rightchild);
		}
	}
	cout << endl;
}

根据二叉树的先、中、后序列，可以得到两个二叉树遍历的性质

（1）已知先序遍历和中序遍历，可以唯一确定一颗二叉树；

（2）已知后序遍历和中序遍历，可以唯一确定一颗二叉树；

4、二叉树的建立

附：创建结点、释放结点

BtNode* BuyNode()   //购买结点
{
	BtNode* node = (BtNode*)malloc(sizeof(BtNode));
	assert(node!=NULL);
	memset(node, 0, sizeof(BtNode));
	return node;
}
void free_node(BtNode* p)//释放结点
{
	free(p);
}

（1）根据输入字符创建树

BtNode* CreateTree1()//根据输入创建二叉树（in:ABC##DE##F##G#H##）
{
	ElemType x;
	BtNode* s = NULL;
	cin >> x;
	if (x!=END)
	{
		s = BuyNode();
		s->data = x;
		s->leftchild = CreateTree1();
		s->rightchild = CreateTree1();
	}
	return s;
}

（2）根据字符串数组创建二叉树

BtNode* CreateTree2(ElemType* &str)//根据字符数组创建二叉树
{
	BtNode* s = NULL;
	if (str != NULL && *str != END)
	{
		s = BuyNode();
		s->data = *str;
		s->leftchild = CreateTree2(++str);
		s->rightchild = CreateTree2(++str);
	}
	return s;
}

（3）根据先序、中序遍历创建二叉树

BtNode*CreateTreePI(ElemType* ps, ElemType* is,unsigned  len)//根据先序、中序遍历创建二叉树
{
	if (ps==NULL||is==NULL||len<1)
	{
		return NULL;
	}
	BtNode* s = BuyNode();
	s->data = *ps;
	int n = 0;
	while (n<len)
	{
		if (*(is+n)==*ps)
		{
			break;
		}
		++n;
	}
	s->leftchild = CreateTreePI(ps + 1, is, n);
	s->rightchild = CreateTreePI(ps + n + 1, is + n + 1, len - n - 1);
	return s;
}

（4）根据中序、后序遍历创建二叉树

int Find_Node(ElemType e,ElemType* is, unsigned  len)//在中序中找到根结点的位置
{
	if (is!=NULL&&len>0)
	{
		for (int i = 0; i < len;++i)
		{
			if (e==*(is+i))
			{
				return i;
			}
		}
	}
	return -1;
}
BtNode*CreateTreeIL(ElemType* is, ElemType* ls, unsigned  len)//根据中序、后序遍历创建二叉树
{
	if (is == NULL || ls == NULL || len<1)
	{
		return NULL;
	}
	BtNode* s = BuyNode();
	s->data = *(ls + len-1);
	int pos = Find_Node(*(ls + len-1),is, len);//在中序中找到根结点的位置
	if (pos==-1)
	{
		return NULL;
	}
	s->leftchild = CreateTreeIL(is,  ls,  pos);
	s->rightchild = CreateTreeIL(is+pos+1, ls+pos, len-pos-1);
	return s;
}

（5）根据已存在的链式二叉树转为顺序存储形式的二叉树结构

void CreateTree_br(BtNode* node, ElemType* br, int len, int pos)//根据链式二叉树建立数组形式的二叉树
{
	if (node == NULL || br == NULL || len<1)        //pos:在数组中的下标位置
	{
		return;
	}
	br[pos] = node->data;
	if (pos*2+1<len)
	{
		CreateTree_br(node->leftchild, br, len, pos * 2 + 1);
	}
	if (pos * 2 + 2<len)
	{
		CreateTree_br(node->rightchild, br, len, pos * 2 + 2);
	}
}

（6）根据已存在的顺序存储形式的二叉树结构转为链式二叉树

BtNode* Create_tree(ElemType *ar, int n,int pos)//int
{
	
	if (ar!=NULL&&pos<n)
	{
		BtNode* s = BuyNode();
		s->data = ar[pos];
		s->leftchild = Create_tree(ar, n, pos * 2 + 1);
		s->rightchild = Create_tree(ar, n, pos * 2 + 2);
		return s;
	}
	return NULL;
}