NB的十进制矩阵快速幂（牛客多校联赛第五场B题）

最新推荐文章于 2022-04-05 11:43:23 发布

原创最新推荐文章于 2022-04-05 11:43:23 发布 · 177 阅读

CC 4.0 BY-SA版权

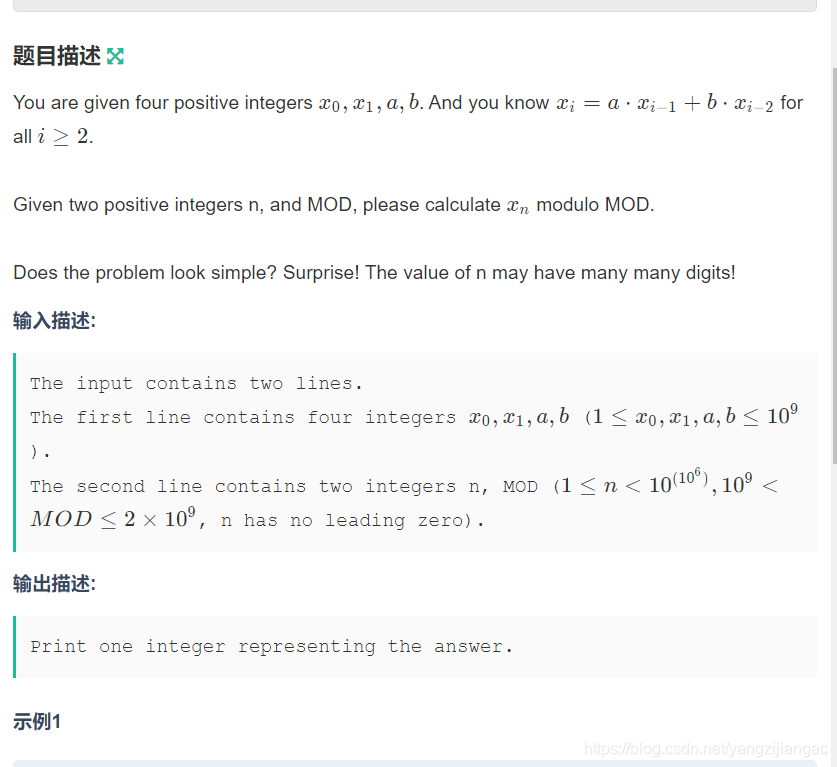
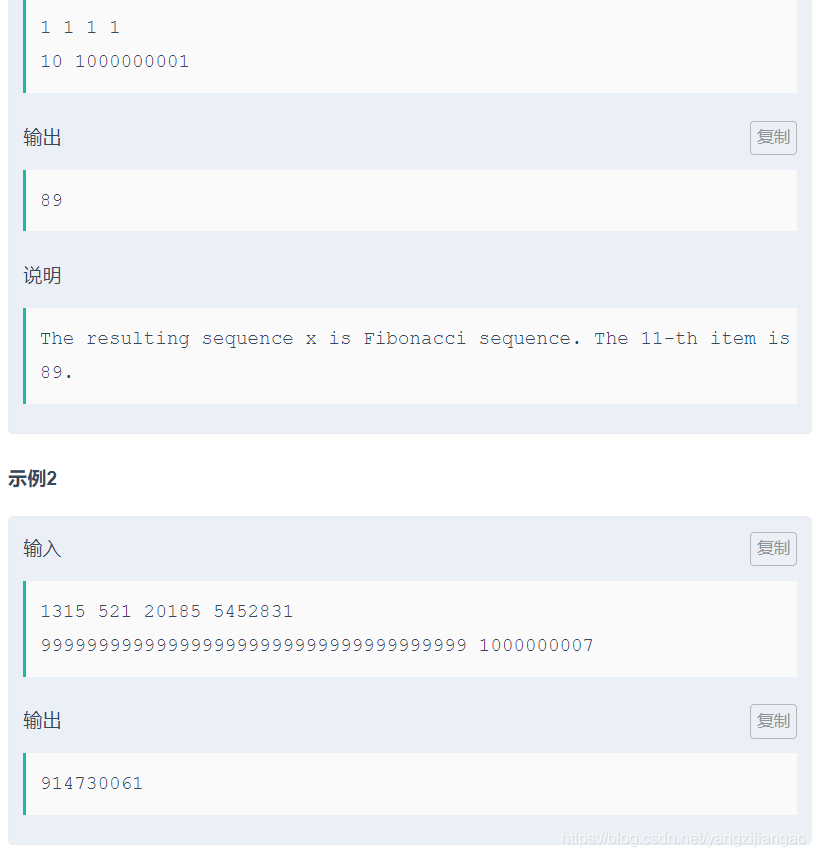
在这里插入图片描述

啰嗦：看到这题的一瞬间我就get到了它的点，矩阵快速幂，因为我所理解的矩阵快速幂是根据快速幂转变而来的所以，它是根据折半的思想写的，当看到这题，我给我的队友mh说矩阵快速幂，然后他就很快的实现了，幸喜之余就提交了，没想到wa了，第二个样例没看到，woc，呢么大的数写个屁啊…之后也想到了再分的写法，但我觉的会T，唉还是太菜
题解：
第二个样例呢么大的数该怎么办呢，其实很简单10进制矩阵快速幂
9999999999999999999999
先让矩阵幂9,在让矩阵幂10因为是递×关系所以就这样就OK了
AC代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1e6+10;
const int INF=0x3f3f3f3f;
typedef long long ll;
ll mod;
struct mat
{
    int m[3][3];
    mat()
    {
        memset(m,0,sizeof(m));
    }
    friend mat operator*(mat x,mat y)
    {
        mat ans;
        for(int i=1;i<=2;++i)
        {
            for(int j=1;j<=2;++j)
            {
                for(int k=1;k<=2;++k)
                {
                    ans.m[i][k]=(ans.m[i][k]+1ll*x.m[i][j]*y.m[j][k])%mod;
                }
            }
        }
        return ans;
    }
};
mat quick_pow(mat a,int b)
{
    mat ans;
    ans.m[1][1]=1;
    ans.m[2][2]=1;
    while(b)
    {
        if(b&1) ans=a*ans;
        a=a*a;
        b>>=1;
    }
    return ans;
}
int main()
{
    int x0,x1,a,b;
    char n[maxn];
    scanf("%d%d%d%d",&x0,&x1,&a,&b);
    scanf("%s%lld",n,&mod);
    mat t,ans;
    int len=strlen(n);
    ans.m[1][1]=1;
    ans.m[2][2]=1;
    t.m[1][1]=0;
    t.m[1][2]=1;
    t.m[2][1]=b;
    t.m[2][2]=a;
    for(int i=len-1;i>=0;--i)
    {
        ans=ans*quick_pow(t,n[i]-'0');
        t=quick_pow(t,10);
    }
    printf("%lld\n",(1ll*x0*ans.m[1][1]+1ll*x1*ans.m[1][2])%mod);
}