实验目的
- 实验内容
八数码问题也称为九宫问题。在3×3的棋盘,摆有八个棋子,每个棋子上标有1至8的某一数字,不同棋子上标的数字不相同。棋盘上还有一个空格,与空格相邻的棋子可以移到空格中。要求解决的问题是:给出一个初始状态和一个目标状态,找出一种从初始状态转变成目标状态的移动棋子步数最少的移动步骤。 - 实验要求
分别利用宽度优先搜索和有序搜索算法求解八数码难题,给出搜索树,并给出从初始节点到目标节点的路径。
实验设备及软件环境
#####1. 电脑配置:
(1)处理器 : Intel i5-4210U CPU @ 1.70GHz, 2.40GHz
(2)安装内存: 8.00GB
(3)操作系统: Windows 10
(4)编程语言: Python
(5)软件环境: python 3.5 、numpy、matplotlib、scipy、Axure 7.0
(6)IDE : PyCharm 5.0.1
实验方法
-
算法描述
(1) 宽度优先搜索
如果搜索是以接近起始节点的程度依次扩展节点的,那么这种搜索就叫做宽度优先搜索。这种搜索是逐层进行的,在对下一层的任一节点进行搜索之前,必须搜索完本层的所有节点。
(2) 有序搜索
令 f ( n ) f(n) f(n) 表示节点 n n n的估价函数值,估算节点希望程度的量度。本次实验选择的 f ( n ) f(n) f(n)的函数形式为:
f ( n ) = g ( n ) + h ( n ) f(n) = g(n) + h(n) f(n)=g(n)+h(n)
其中, g ( n ) g(n) g(n)为初始节点到当前节点的路径长度(深度), h ( n ) h(n) h(n)为当前节点“不在位”的将牌数。
有序搜索(ordered search),即最好优先搜索, 选择Open表上具有最小f值的节点作为下一个要扩展的节点。 -
流程图
(1) 宽度优先搜索
(2) 有序搜索
- 程序代码 (python)
(1) 宽度优先搜索
__author__ = 'ysc'
import numpy as np
class State:
def __init__(self, state, directionFlag=None, parent=None):
self.state = state
# state is a ndarray with a shape(3,3) to storage the state
self.direction = ['up', 'down', 'right', 'left']
if directionFlag:
self.direction.remove(directionFlag)
# record the possible directions to generate the sub-states
self.parent = parent
self.symbol = ' '
def getDirection(self):
return self.direction
def showInfo(self):
for i in range(3):
for j in range(3):
print(self.state[i, j], end=' ')
print("\n")
print('->')
return
def getEmptyPos(self):
postion = np.where(self.state == self.symbol)
return postion
def generateSubStates(self):
if not self.direction:
return []
subStates = []
boarder = len(self.state) - 1
# the maximum of the x,y
row, col = self.getEmptyPos()
if 'left' in self.direction and col > 0:
#it can move to left
s = self.state.copy()
temp = s.copy()
s[row, col] = s[row, col-1]
s[row, col-1] = temp[row, col]
news = State(s, directionFlag='right', parent=self)
subStates.append(news)
if 'up' in self.direction and row > 0:
#it can move to upper place
s = self.state.copy()
temp = s.copy()
s[row, col] = s[row-1, col]
s[row-1, col] = temp[row, col]
news = State(s, directionFlag='down', parent=self)
subStates.append(news)
if 'down' in self.direction and row < boarder: #it can move to down place
s = self.state.copy()
temp = s.copy()
s[row, col] = s[row+1, col]
s[row+1, col] = temp[row, col]
news = State(s, directionFlag='up', parent=self)
subStates.append(news)
if self.direction.count('right') and col < boarder: #it can move to right place
s = self.state.copy()
temp = s.copy()
s[row, col] = s[row, col+1]
s[row, col+1] = temp[row, col]
news = State(s, directionFlag='left', parent=self)
subStates.append(news)
return subStates
def solve(self):
# generate a empty openTable
openTable = []
# generate a empty closeTable
closeTable = []
# append the origin state to the openTable
openTable.append(self)
steps = 1
# start the loop
while len(openTable) > 0:
n = openTable.pop(0)
closeTable.append(n)
subStates = n.generateSubStates()
path = []
for s in subStates:
if (s.state == s.answer).all():
while s.parent and s.parent != originState:
path.append(s.parent)
s = s.parent
path.reverse()
return path, steps+1
openTable.extend(subStates)
steps += 1
else:
return None, None
if __name__ == '__main__':
# the symbol representing the empty place
# you can change the symbol at here
symbolOfEmpty = ' '
State.symbol = symbolOfEmpty
# set the origin state of the puzzle
originState = State(np.array([[2, 8, 3], [1, 6 , 4], [7, symbolOfEmpty, 5]]))
# and set the right answer in terms of the origin
State.answer = np.array([[1, 2, 3], [8, State.symbol, 4], [7, 6, 5]])
s1 = State(state=originState.state)
path, steps = s1.solve()
if path: # if find the solution
for node in path:
# print the path from the origin to final state
node.showInfo()
print(State.answer)
print("Total steps is %d" % steps)
(2)有序搜索算法
__author__ = 'ysc'
import numpy as np
class State:
def __init__(self, state, directionFlag=None, parent=None, depth=1):
self.state = state
# state is a ndarray with a shape(3,3) to storage the state
self.direction = ['up', 'down', 'right', 'left']
if directionFlag:
self.direction.remove(directionFlag)
# record the possible directions to generate the sub-states
self.parent = parent
self.symbol = ' '
self.answer = np.array([[1, 2, 3], [8, State.symbol, 4], [7, 6, 5]])
self.depth = depth
# calculate the num of elements which are not in the proper position
num = 0
for i in range(len(state)):
for j in range(len(state)):
if self.state[i, j] != ' 'and self.state[i, j] != self.answer[i, j]:
num += 1
self.cost = num + self.depth
def getDirection(self):
return self.direction
def showInfo(self):
for i in range(3):
for j in range(3):
print(self.state[i, j], end=' ')
print("\n")
print('->')
return
def getEmptyPos(self):
postion = np.where(self.state == self.symbol)
return postion
def generateSubStates(self):
if not self.direction:
return []
subStates = []
# the maximum of the x,y
row, col = self.getEmptyPos()
if 'left' in self.direction and col > 0:
#it can move to left place
s = self.state.copy()
temp = s.copy()
s[row, col] = s[row, col-1]
s[row, col-1] = temp[row, col]
news = State(s, directionFlag='right', parent=self, depth=self.depth+1)
subStates.append(news)
if 'up' in self.direction and row > 0:
#it can move to upper place
s = self.state.copy()
temp = s.copy()
s[row, col] = s[row-1, col]
s[row-1, col] = temp[row, col]
news = State(s, directionFlag='down', parent=self, depth=self.depth+1)
subStates.append(news)
if 'down' in self.direction and row < boarder:
#it can move to down place
s = self.state.copy()
temp = s.copy()
s[row, col] = s[row+1, col]
s[row+1, col] = temp[row, col]
news = State(s, directionFlag='up', parent=self, depth=self.depth+1)
subStates.append(news)
if self.direction.count('right') and col < boarder:
#it can move to right place
s = self.state.copy()
temp = s.copy()
s[row, col] = s[row, col+1]
s[row, col+1] = temp[row, col]
news = State(s, directionFlag='left', parent=self, depth=self.depth+1)
subStates.append(news)
return subStates
def solve(self):
# generate a empty openTable
openTable = []
# generate a empty closeTable
closeTable = []
# append the origin state to the openTable
openTable.append(self)
# denote the steps it travels
steps = 0
while len(openTable) > 0: # start the loop
n = openTable.pop(0)
closeTable.append(n)
subStates = n.generateSubStates()
path = []
for s in subStates:
if (s.state == s.answer).all():
while s.parent and s.parent != originState:
path.append(s.parent)
s = s.parent
path.reverse()
return path, steps+1
openTable.extend(subStates)
# sort the openTable in terms of the cost
openTable.sort(key=lambda x: x.cost)
steps += 1
else:
return None, None
if __name__ == '__main__':
# the symbol representing the empty place
symbolOfEmpty = ' '
# you can change the symbol at here
State.symbol = symbolOfEmpty
# set the origin state of the puzzle
originState = State(np.array([[2, 8, 3], [1, 6 , 4], [7, symbolOfEmpty, 5]]))
State.answer = np.array([[1, 2, 3], [8, State.symbol, 4], [7, 6, 5]])
s1 = State(state=originState.state)
path, steps = s1.solve()
if path: # if find the solution
for node in path:
# print the path from the origin to final state
node.showInfo()
print(State.answer)
print("Total steps is %d" % steps)
实验结果
绘图软件为:Axure 7.0
- 搜索树
(1)DFS
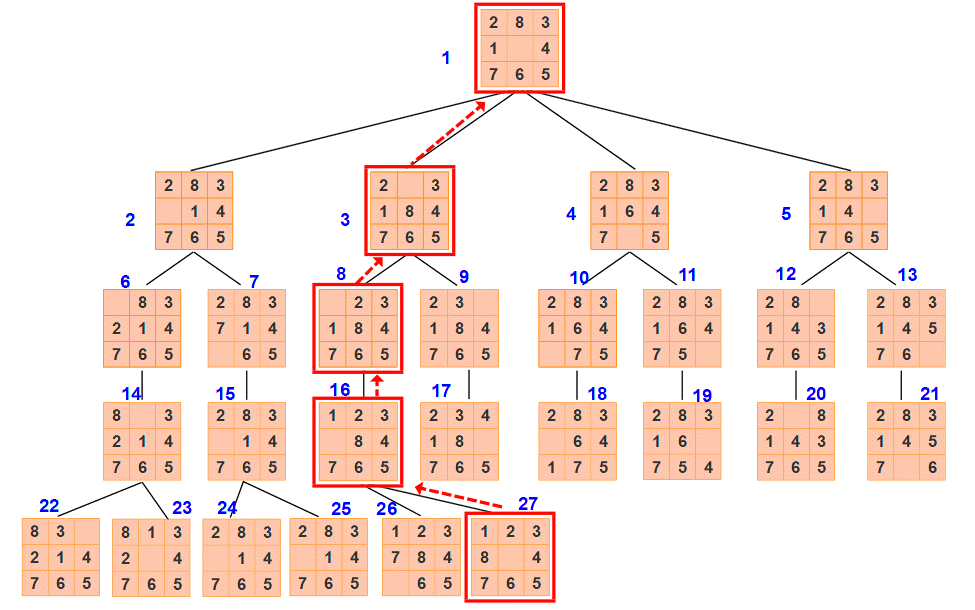
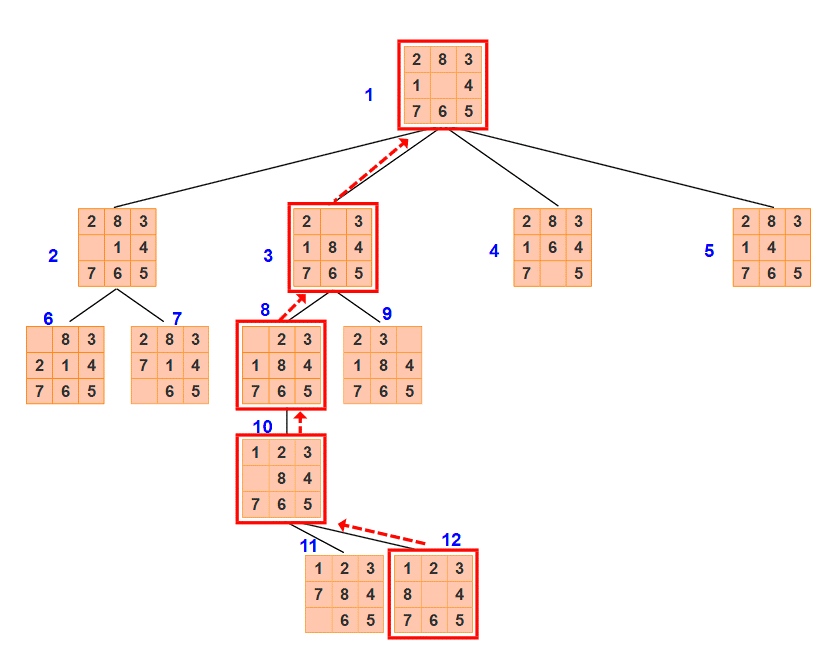
(2) 有序搜索
- 搜索路径
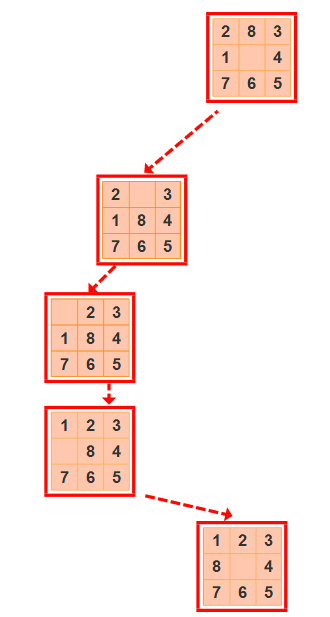
实验分析
- 结果分析
(1) 宽度优先搜索
由实验结果可知,宽度优先搜索扩展节点个数为4,生成节点个数为26。
(扩展节点:路径中的节点数-1;生成节点:搜索树中节点数目-1)
(2) 有序搜索
由实验结果可知,有序搜索扩展节点个数为4,生成节点个数为12。
(扩展节点:路径中的节点数-1;生成节点:搜索树中节点数目-1)
2. 方法特点
(1) 宽度优先搜索 - 宽度优先搜索又称广度优先搜索,“广度”一词形象地揭示了这种搜索是逐层进行的:在对下一层的任一节点进行搜索之前,必须搜索完本层的所有节点。
- 不需要重排Open表
- 一般只适用于求解比较简单的问题。
- 若问题有解,宽度优先搜索一定可以求得,并且求出的是最优解。
(2) 有序搜索
有序搜索利用到启发式信息,对Open表中元素进行了重排,选择最有希望的节点加以扩展,搜索效率较盲目搜索大为提高。
3. 区别
宽度优先搜索属于盲目搜索,没有利用到启发信息,故效率较低;而有序搜索利用到节点本身的特性,将其作为启发式信息,对Open表进行重排,每一次选择都是最优的,具有贪心性质,搜索效率大为提高。
结论
综上所述,可以明显看出宽度优先搜索与有序搜索的效率差异。这启示我们在解决生活问题时,不仅仅是需要找到一个通用的(general)算法框架,因为虽然可以求出解,但是效率很低,我们更需要根据实际问题具体分析,通过问题本身,提炼出更有效的启发式信息,这样才能提高解的效率。





 本文介绍了使用Python解决八数码难题,分别利用宽度优先搜索和有序搜索算法,给出了搜索树和从初始节点到目标节点的路径。实验结果显示,有序搜索在扩展节点个数和生成节点个数上优于宽度优先搜索,表明有序搜索的效率更高。
本文介绍了使用Python解决八数码难题,分别利用宽度优先搜索和有序搜索算法,给出了搜索树和从初始节点到目标节点的路径。实验结果显示,有序搜索在扩展节点个数和生成节点个数上优于宽度优先搜索,表明有序搜索的效率更高。
















 5346
5346

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








