八数码难题（上）：无信息搜索【python实现】

什么是八数码难题？

八数码问题（Eight Puzzle Problem）是诺耶斯·帕尔默·查普曼在19世纪70年代发明和推广的谜题。所谓八数码是指一个3x3的九宫格，有8个标有1到8的正方形块和一个空白正方形（x）。问题的目标是重新排列积木，使其井然有序。如：

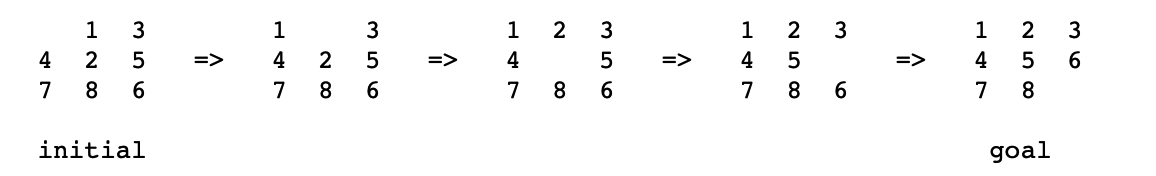
The 8-puzzle problem is a puzzle invented and popularized by Noyes Palmer Chapman in the 1870s. It is played on a 3-by-3 grid with 8 square blocks labeled 1 through 8 and a blank square. Your goal is to rearrange the blocks so that they are in order. You are permitted to slide blocks horizontally or vertically into the blank square. The following shows a sequence of legal moves from an initial board position (left) to the goal position (right).

什么是无信息搜索？

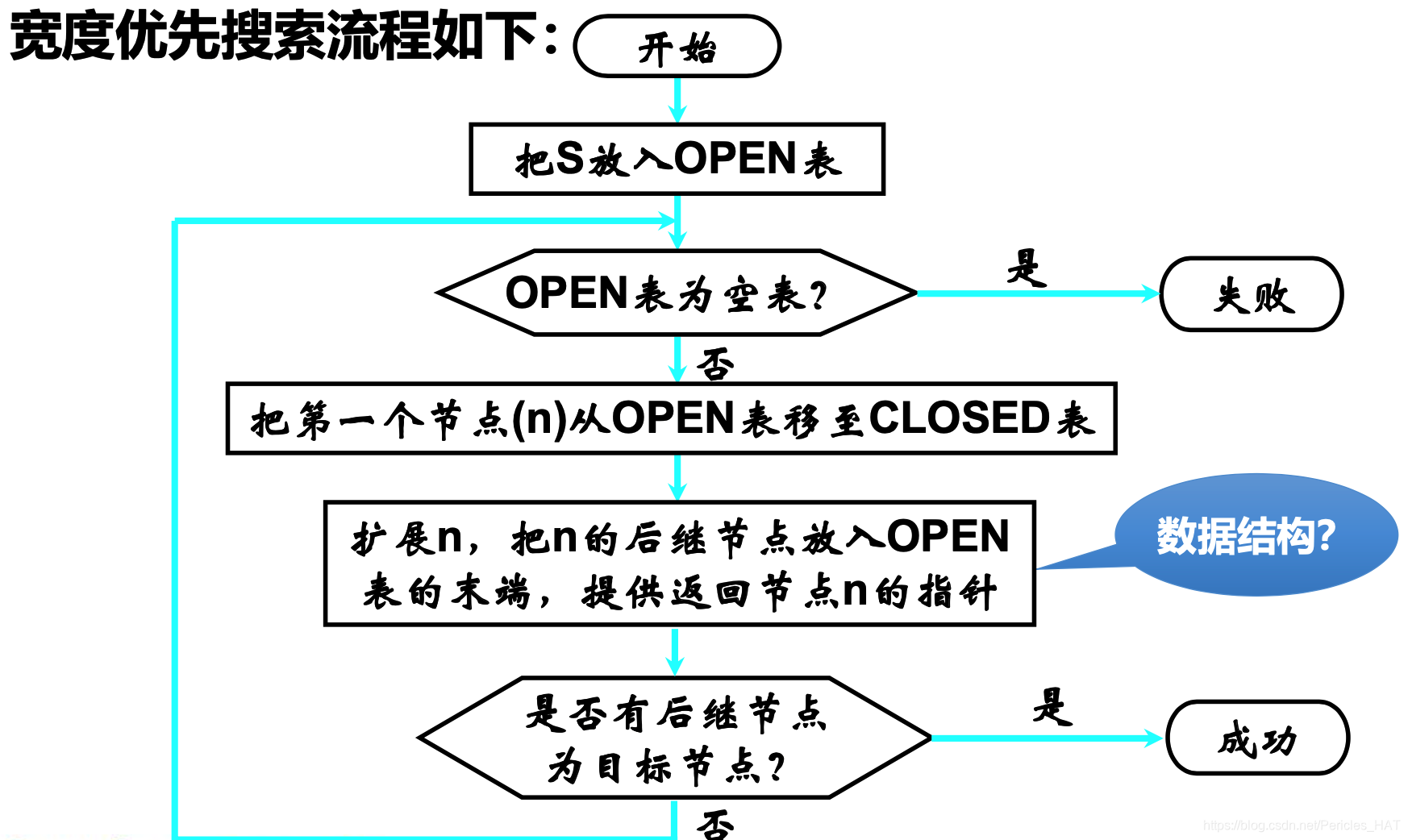
无信息搜索也被称为盲目搜索，该术语（无信息、盲目的）意味着该搜索策略没有超出问题定义提供的状态之外的附加信息。所有能做的就是生成后继节点，并且区分一个目标状态或一个非目标状态。
无信息搜索主要包括DFS、BFS、UCS等方法。

深度优先（stack）、广度优先（queue）：

• 扩展节点集（OPEN表）大小：DFS（b*m），BFS（b^m）
• 完备性：BFS具有，DFS在无环下具有
• 最优性：BFS具有

一致代价搜索（priority queue / heap）：

• Uniform-Cost Search，应用于有权图
• 将最小值g(i)的节点i从OPEN表移到CLOSE表（优先队列，堆）
• 宽搜是其特殊形式（即代价为1）
• 搜索到终点还不能停止，须排除其他路径的代价
• 性质和BFS类似

迭代加深、双向搜索等

以BFS为例子解八数码问题

1. 先将八数码问题抽象化。我们定义输入格式为“12345x786”这样的字符串代表：

2. 使用BFS解八数码，首先我们要明确其实现方法。我们用一个列表q模拟队列OPEN表，用一个字典d模拟哈希表（hash table / unordered_map）来存储<state, distance>的“状态-距离”表，用一个字典p模拟一棵树存储BFS的全部遍历结果。
   

q = [] # string
d = {
   
   } # <string, int>
p = {
   
   } # <string, string> (son -> father)

3. 模拟移动。我们用除法向下取整和取模的方法，将字符串的下标映射到九宫格的坐标，然后再用四个向量模拟上下左右四个方向的移动。通过遍历四个方向达到“搜索”的效果。

t = q[0] # t是诸如“1234567x8”的字符串
k = t.find('x') # 找到x在t中的下标
x = int(k / 3)
y = k % 3
# 左、右、上、下
dx = [1, -1, 0, 0]
dy = [0, 0, 1, -1]

4. 用层次遍历方法模拟队列的先进先出原则（FIFO）。

while q:
	t = q[0]
	q.pop