洛谷P2532 [AHOI2012]树屋阶梯

最新推荐文章于 2022-02-25 23:27:11 发布

原创最新推荐文章于 2022-02-25 23:27:11 发布 · 419 阅读

1 ·

CC 4.0 BY-SA版权

本文为博主原创文章，未经博主允许不得转载。

数论同时被 2 个专栏收录

34 篇文章

订阅专栏

高精度

1 篇文章

订阅专栏

本文介绍了一种使用卡特兰数解决树屋阶梯搭建问题的方法。通过数学推导，将问题转化为卡特兰数的计算，并给出了具体的实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

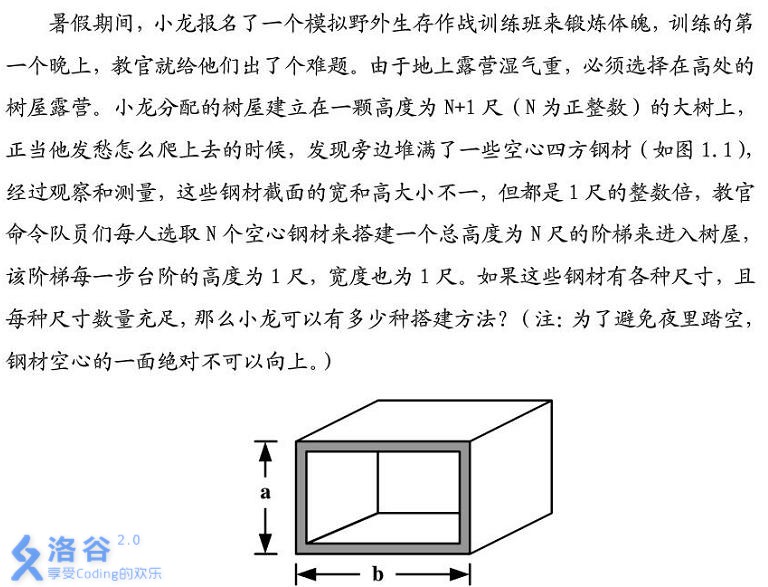
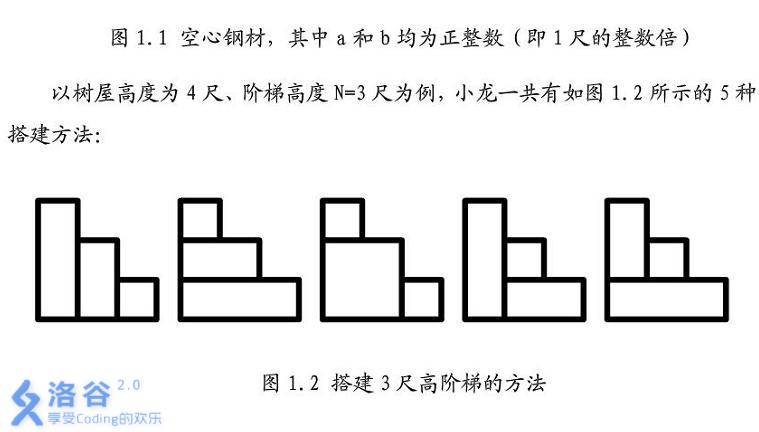
题目描述

输入输出格式

输入格式：

一个正整数N（1<=N<=500），表示阶梯的高度。

输出格式：

一个正整数，表示搭建方法的个数。（注：搭建方法的个数可能很大）

输入输出样例

输入样例#1：

输出样例#1：

说明

40%的数据：1<=N<=20

80%的数据：1<=N<=300

100%的数据：1<=N<=500

正解：卡特兰数+高精乘+gcd

为什么是卡特兰数？

玄学：n=1 , ans=1 ; n=2 , ans=2 ; n=3 , ans=5 ;于是想到了卡特兰数。。。

正解：我们发现对于任何大小为 $i$ 的树屋阶梯，都可以由左上角放一块大小为 $j$ 的以及右下角放一块大小为 $i - j - 1$ 的树屋阶梯，再在空缺的地方由单个大块的矩形填充即可构成，这个构成的树屋阶梯一共有 $(j) + (i - j - 1) + 1$ 个钢材，正好是 $i$ 个。因为 j 可以在 0 到 $i - 1$ 取且可以证明每一个构成的树屋阶梯一定各不相同，所以我们可以得到树屋阶梯方案与大小关系的递推式 $f_{i}$ = $f_{i - 1}$ × $f_{0}$ + $f_{i - 2}$ × $f_{2}$ + ... + $f_{0}$ × $f_{i - 1}$ 。同时，我们规定 $f_{0}$ =f $_{1}$ = 1。哦，这不就是卡特兰数的递推式吗？于是我们就可以安心将这道题当作卡特兰数的模板题食用了。

附代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#define MAXN 510
using namespace std;
int n,a[MAXN],b[MAXN],ans[MAXN*10];
int gcd(int x,int y){
    if(!y)return x;
    return gcd(y,x%y);
}
void mul(int x){
    int c=0;
    for(int i=1;i<=ans[0];i++){
        ans[i]*=x;ans[i]+=c;
        c=ans[i]/10;
        ans[i]%=10;
    }
    while(c){
        ans[++ans[0]]=c%10;
        c/=10;
    }
}
int main(){
    cin>>n;
    for(int i=2;i<=n;i++){a[i-1]=n+i;b[i-1]=i;}
    for(int i=1;i<n;i++)
    for(int j=1;j<n;j++){
        if(b[j]==1)continue;
        int g=gcd(a[i],b[j]);
        if(g!=1){a[i]/=g;b[j]/=g;}
        if(a[i]==1)break;
    }
    ans[0]=ans[1]=1;
    for(int i=1;i<n;i++){
        if(a[i]==1)continue;
        mul(a[i]);
    }
    for(int i=ans[0];i>=1;i--)printf("%d",ans[i]);
	return 0;
}