算法训练营第14天|226.翻转二叉树、101.对称二叉树、104.二叉树的最大深度、111.二叉树的最小深度

感觉越来越难了，树里面最难以理解的我觉得还是对于递归，而且似乎每天抽一点点时间并不能很好的完成打卡的内容，今天又在补昨天欠的了，不管怎样，还是继续坚持吧，加油！

226.翻转二叉树

这一题按照递归三部曲能写出来，但是还是不太明白为什么中序遍历的顺序会导致有些子树翻转两次，我想还是对遍历掌握的不熟。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) {return null;}
        swap(root);
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }

    public void swap(TreeNode node) {
        TreeNode tmp = node.left;
        node.left = node.right;
        node.right = tmp;
    }
}

101.对称二叉树

这一题我听完了算法公开课，花了很长时间试着理解为什么对比的一定是左子树的left和右子树的right，也就是左子树的外侧和右子树的外侧，在一开始树只有三层的时候，我能够理解是比较左子树的left和右子树的right，然后我一直以为如果树的层数多了之后，比如有更多层，这时候还是这样比较吗？

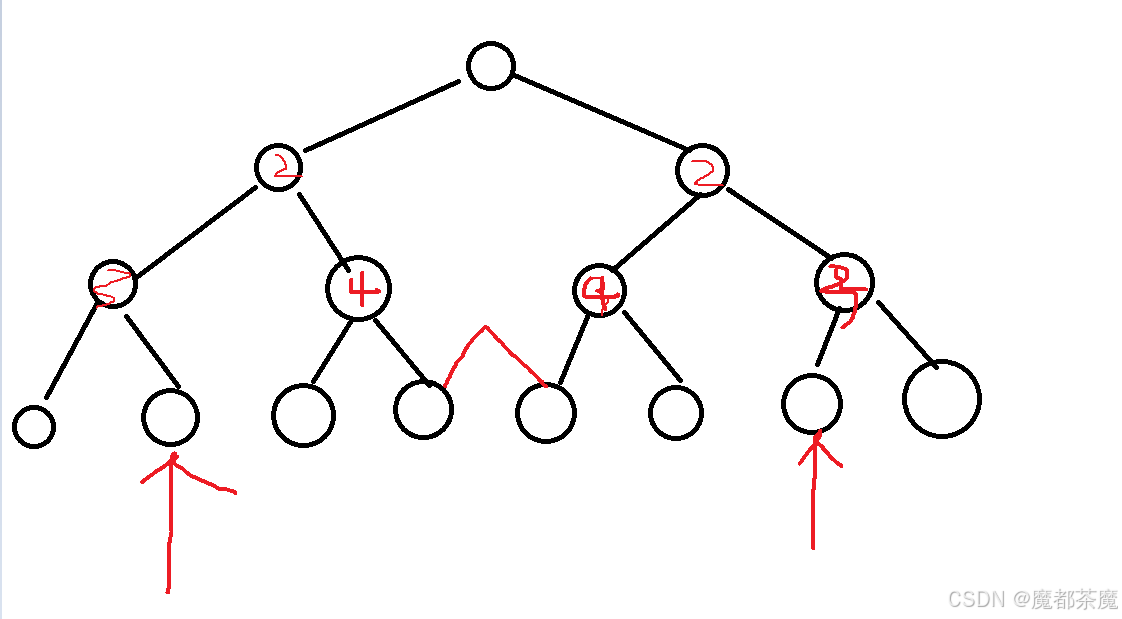
画了个简单的图，因为如果要对称，就必须是左子树和右子树对称，对应的规律就是左子树的左子树和右子树的右子树对称。

package binaryTree;

public class IsSymmetric1Demo {
    public static void main(String[] args) {

    }

    //这一题听了视频讲解，还是不懂，主要是不明白为什么比较的是左边外侧和右边外侧
    //感觉这一题对我来说最大的理解难点并不是比较的单层递归里的逻辑，而是哪两个来比较，后面再听几遍了
    public static boolean isSymmetric1(TreeNode root) {
        return compare(root.left, root.right);
    }

    public static boolean compare(TreeNode left, TreeNode right) {
        if (left == null && right != null) {
            return false;
        }
        if (left != null && right == null) {
            return false;
        }

        if (left == null && right == null) {
            return true;
        }
        if (left.val != right.val) {
            return false;
        }
        // 比较外侧
        boolean compareOutside = compare(left.left, right.right);
        // 比较内侧
        boolean compareInside = compare(left.right, right.left);
        return compareOutside && compareInside;
    }
}

104.二叉树的最大深度

这个题还是递归，不理解递归就不知道咋写，看了代码感觉很简单，悲剧。。。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth, rightDepth) + 1;
    }
}

111.二叉树的最小深度

又去看了下讲解，理解了最小深度的计算方式，主要是最小深度找到的叶子节点必须是左右子节点均为NULL的，否则会把没有左或者右其中之一个孩子的父节点认为是最小深度，也就是代码里的root.left或者root.right == null 时，返回的应该是相应的另外一个子树的深度。

public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);
        if (root.left == null) {
            return rightDepth + 1;
        }
        if (root.right == null) {
            return leftDepth + 1;
        }
        // 左右结点都不为null
        return Math.min(leftDepth, rightDepth) + 1;
    }