算法训练营第二天 | 209.长度最小的子数组、59.螺旋矩阵II

今天是算法训练营第二天(其实是第三天，主要第二天我有事没来得及记录~~)

209.长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 

子数组

 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

这一题一开始上来就尝试用暴力解法，写了一大堆，后面发现没审清题意，竟然是总和大于等于的....所以做算法题真的有两点特别忌讳：

1.审题不全或者不清；

2.算法没理清楚就开始码代码。

题意看清楚之后，暴力解法其实代码不难，但是很容易超时，如果数组长度特别大的话。

看了Carl老师的讲解之后，理解了下滑动窗口的思想，我大致按照我的理解记一下看看：

1.滑动窗口有两个要点，一是窗口的结束位置，二是窗口的起始位置；

2.在这个题目里，我们先用一个for循环来遍历，往后逐渐累加元素的和，找到大于等于目标值的位置后，先停下来，这时候的位置其实就是窗口的结束位置了，记为j；

3.因为题干是要找最小长度，所以，结束位置固定之后，开始从0开始移动起始位置，直到找到最大的起始位置记为i，此时j-i+1就是第一遍找到截止终止位置j时满足条件的最小子串；

4.外层的for循环继续往后，j的位置逐渐增加，这里有个注意点是起始位置不需要从0开始了，就从上一轮的起始位置开始就行。

怎么理解呢？因为第一次的j只要往后移动一位，意味着从当时的起始位置i到j+1，无论怎么找都已经比前一次的最小子串要长了，所以找最小子串，不需要把i再回退到0开始，就从上一个i的位置开始就行了。(这个其实就是数学的推导吧，我个人认为)。

详细代码如下：

public static int minSubArrayLen(int target, int[] nums) {
        int result = Integer.MAX_VALUE;
        int left = 0; //滑动窗口的起始位置
        int sum = 0;//保存累加的和
        for(int i = 0; i < nums.length; i++) {
            sum += nums[i];//不断地向后移动i，累加结果
            while(sum >= target) {//此时累加的结果已经>=target了，i的位置可以停下来
                System.out.println("此时进入while循环时的i为：" + i);
                result = Math.min(result,i - left + 1);
                sum -= nums[left++];//这里，一句代码实现两个功能，先把left下标的值减掉，在把left加1，学到了。
            }// 此时返回的结果是在终止位置i时的最小的区间result
            //之后，代表终止位置的i继续往后移动，但是起始位置的left不用从0开始了

        }
        return result == Integer.MAX_VALUE ? 0 : result;
    }

59.螺旋矩阵

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

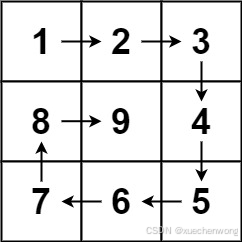
这一题上来我是非常懵逼的，本来的想法是，建好一个n*n的二维数组，然后推导出一个数学公式，从1遍历到n*n时一个一个的往二维数组对应位置放相应的数就行了，结果推导了半天，依旧是懵逼状态，搞不定公式。

只好接着去看Carl老师的视频介绍(我真是菜，哈哈。。)，这种螺旋矩阵做法竟然是一圈一圈，一条边一条边的去遍历塞值，遍历的要点有三个：

1.遍历的圈数，其实就是n/2，因为每次遍历一圈，减少了2行；

2.遍历的边界条件，四条边分别遍历时，这里统一的处理做法是采用左闭右开，也就是每条边只处理从第一个到倒数第二个数，最后一个数交给下一条边作为第一个数来处理；

3.遍历终止时，如果N为奇数，会存在最中心的一个点需要单独处理下;

四条边按照固定的顺序遍历，填好边界条件和赋值就好了，具体代码如下：

public static int[][] generateMatrix(int n) {
        int[][] nums = new int[n][n]; //初始化一个n*n的矩阵
        //螺旋矩阵的难点在于每次遍历边的时候需要控制边界条件，听了Carl老师的讲解，明白了需要用
        //一个统一的边界控制条件来循环遍历，这里使用的是左闭右开，也就是每一条边只处理第一个到倒数第二个数
        //每条边的最后一个数交给下一条边作为第一个数来处理

        int startx = 0,starty = 0;
        int offset = 1; //定义每条边的偏移量，起始就是从最外层往内层循环的次数

        int loop = 1;//循环次数
        int i,j; //代表横纵坐标，i-行，j-列
        int count = 1; //循环要填入的数
        while(loop <= n/2) {
            //遍历最上面的一条边,横坐标不动，纵坐标往右逐次增加移动
            for(j = starty;j < n - offset; j++) {
                nums[startx][j] = count++;
            }

            //遍历最右面的边，j不动，i逐次增加，此时j已经等于n-offset了
            for(i = startx; i < n-offset; i++) {
                nums[i][j] = count++;
            }

            //遍历最下面的边，j逐次减小，i不动，此时i已经等于n-offset了
            for(;j > starty; j--) {
                nums[i][j] = count++;
            }

            //处理最左面的边，j不动，i减少，此时j等于starty了
            for(;i > startx; i--) {
                nums[i][j] = count++;
            }

            //一圈循环完之后，控制变量，此时偏移量offset需要+1，startx和starty也需要+1
            startx ++;
            starty ++;

            offset ++;

            //循环次数也要加1
            loop ++;
        }

        if (n % 2 == 1) { // n 为奇数时，单独处理矩阵中心的值
            nums[startx][starty] = count;
        }

        return nums;
    }

今天的迟到打开就到这了~~