（令人头疼的）按位与&，或|，异或^ 的应用

Hard but lovely

已于 2025-06-17 14:25:25 修改

阅读量1k

点赞数 20

CC 4.0 BY-SA版权

文章标签： java 算法开发语言

于 2025-06-16 18:33:41 首次发布

本文链接：https://blog.youkuaiyun.com/xuandonggo/article/details/148694485

前言二进制

二进制到10进制

二进制：首先类比我们属性的10进制，如 123----- 可以写成 1*10^2+2*10^1+3*10^0;

这样你理解啦十进制位是如何描述的，我们习惯用的加减法也是10进制位的因为满10进位，所以我们类似写一个二进制位，然后把他们算出来在相加就是我们习惯的十进制了。

写一个二进制： 1010： 0*2^0 +1*2^1+0*2^2+1*2^3 = 10 这就是二进制到十进制的转换，我们这样理解就很简单了。

10进制到二进制

就是逆过程了我们看看下面这些位对应的10进制数： 1111： 8 4 2 1

2^3, 2^2,2^1,2^0 ，如果我们现在要用二进制描述10 就是8+2 那对应的位写成1 其他写成0就行了， -----》1010

对二进制位的进一步理解

刚刚我们描述一个10进制数的时候，我们是通过二进制位描述它，每一个位对应一个10进制数值对吧，这个位存在就写成1，不存在就写成0.

这个思想很重要存在！于不存在，这也很类似真假的过程，0为假，1为真，同样的，0存在，1不存在。

二进制位我们现在知道类比十进制位学习，现在随便写一个2138213721 这个十进制数，它有10位每一位对应的值都是10以内的对吧，我们计算机存储数据，我们一个位就能存2个数字，要么是1要么是0，但是如果我们用连续的数字去存放二进制位，0000 这里是4位，那数值的取值范围就从0 - 1111（15）那在多一位 5个二进制位就变成了： 0-11111（31）表示的范围就大了

：所以定义一些变量让他有固定的位数也就意味着它有固定的空间比如 int（4个字节，32位）

表示的数据范围就很大了。char 1个字节

下面介绍对二进制位操作的运算符，&，|，取反~（二进制位区分一般结合&用），^

左移（<<）与右移（>>）操作详解

1. 左移操作（a << n）

规则：将二进制位整体向左移动 n 位，右侧补 0。
效果：数值相当于乘以 2ⁿ（仅适用于未溢出的情况）。

示例：

cpp

运行

5 << 2  // 二进制：0101 → 左移2位 → 010100（十进制20）

用途：快速计算乘法（如 a << 3 等价于 a * 8）、设置标志位（如 1 << n 生成第 n 位为 1 的掩码）。

2. 右移操作（a >> n）

规则：将二进制位整体向右移动 n 位，左侧补位分两种情况：
- 逻辑右移：补 0（适用于无符号类型）。
- 算术右移：补符号位（适用于有符号类型，保持负数的符号）。
效果：数值相当于除以 2ⁿ（向下取整）。

示例：

cpp

运行

20 >> 2  // 二进制：010100 → 右移2位 → 0101（十进制5）
-8 >> 2  // 二进制：11111000（补码） → 右移2位 → 11111110（十进制-2）

-8>>2 结果是-2 相当于 -8》》-2

用途：快速计算除法、提取特定位（如 (num >> 3) & 1 获取第 3 位）。

3. 关键区别

操作	符号位处理	典型应用场景
`<<`	不影响符号位（溢出可能改变符号）	快速乘法、生成掩码
`>>`	逻辑右移补 0，算术右移补符号位	快速除法、位提取

一、按位与（&）的意义

首先你得对二进制有一定的了解，如

同一则为1，有0就0 如111 &011 == 011 相当于左侧有的右侧也得有才会存在只

1. 逻辑层面：交集与筛选

逐位比较时，仅当两位均为 1 时结果为 1，本质是取两个数的二进制 “公共部分”。

类比：如两个集合的交集，仅保留同时存在的元素。

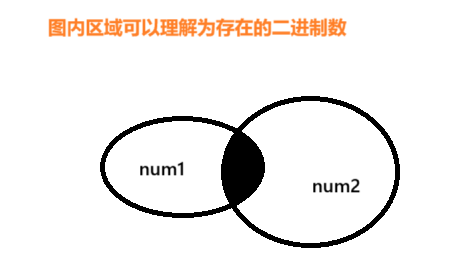
看图2我做了啥，----------------》我对num2进行取反操作就是~ 然后在求他们的交集，也就意味着

只取出来num1 然后去除公共部分--这个思想很有用哦。

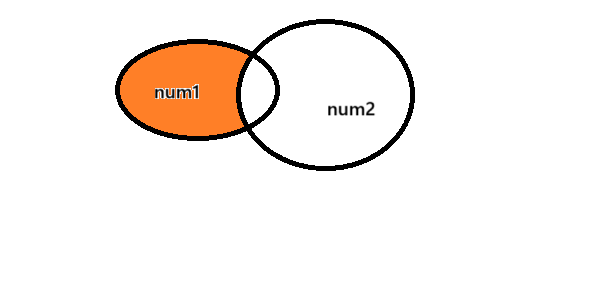
想象一下我们写一个32位的1111 然后拿他去冲击任意一个32位的数数字对吧，那么这个数字只有最后几位会被原封不动的被保留下来。这用来数据提取。

另一个如果我们对这个32位的1111 进行取反也就意味着这个数1111全部是0其他是1，这样就导致呢，它存在的反而被冲击的数字位数不能有。这个用来通过掩码清空特定位

2. 典型应用

2.1 状态判断：检查特定标志位是否开启。
例：(flags & 0x01) != 0 用于判断最低位是否为 1（如奇偶性）。

bool iseven(int i)
{
	// 判断是不是偶数
	return (i & 1) == 0;
}

2.2 清空特定位：将某些位强制置 0。
例：num & ~0b100 可将第 3 位清 0（~为按位取反）。

2.3 数据提取：通过固定二进制位提取目标数据。

2.3.1 获取整数的全部二进制数

void test01()
{
   // 提取整数的每一位 
	// 我们的&每一次都是保留大家公有的所以如果我拿 1去&其他的
	// 然后遍历全部位 就可以得到了 
	 //  1除了最后一位是1其他全是0 所以我们一位一位的得到就行
	int n = 127;// 得到它的二进制位 32位
	vector<int> v(32,0);
	
	for (int i = 31;i >=0;i--)
	{
		int r = n & 1;
		n >>= 1;
		v[i] = r;
		
	}
	vector<int>::iterator it = v.begin();
	while (it != v.end())
	{
		cout << *it ;
		it++;
	}



}

二、按位或（|）的意义

1. 逻辑层面：有1则为1

逐位比较时，只要有一位为 1 结果即 1，本质是合并两个数的二进制 “存在部分”。

合并：

类比：如两个集合的并集，保留所有出现的元素。

2. 典型应用

标志位设置：将特定位置为 1 而不影响其他位。
例：flags | 8（1111）强制开启第 4 位，其他位不变。
权限组合：叠加多个独立权限。
如文件权限中，read（0b100）| write（0b010）| execute（0b001） 组合为0b111（7）。
数据合并：拼接不同字段的二进制值。
例：将两个 8 位数据合并为 16 位：(high << 8) | low。

三、对比与核心差异

操作	逻辑本质	核心作用	典型场景
按位与（&）	取公共位（交集）	提取、判断、清位	掩码操作、状态检测
** 按位或（	）**	取并集（叠加）	设置、组合、合并	标志位控制、权限叠加