7-2 二叉搜索树的插入序列
二叉搜索树定义为:
左子树仅包含小于根结点的元素;
右子树仅包含大于根结点的元素;
左右子树均为二叉搜索树。
一棵二叉搜索树可以有不同的插入顺序。例如,对于如下的二叉搜索树
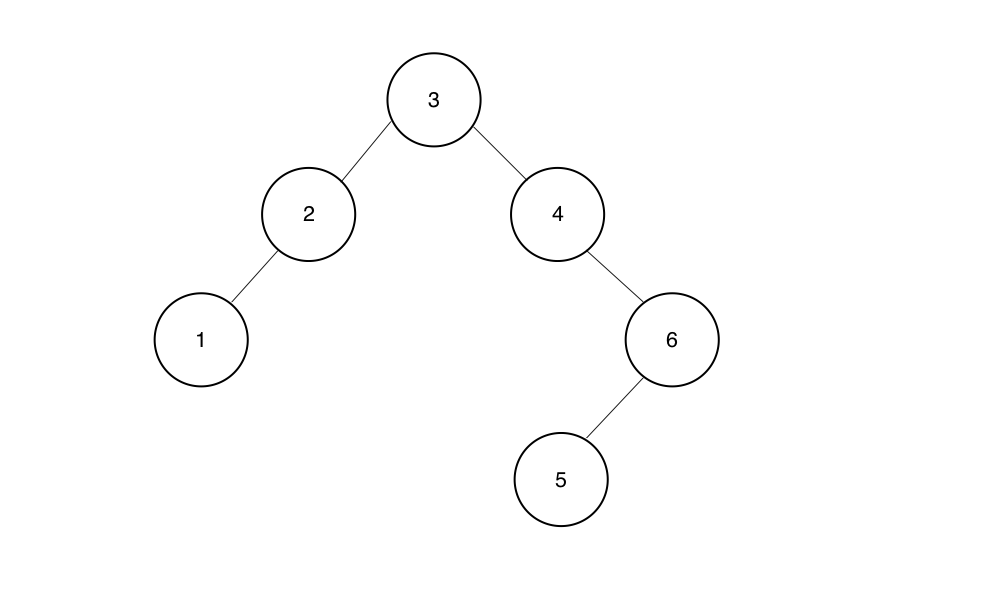
插入序列可以是 3 2 1 4 6 5, 也可以是 3 2 4 1 6 5 但不可以是 3 2 4 5 6 1。
下面给出一棵二叉搜索树的先序遍历序列,请编写程序求出该树的插入序列个数。考虑到总数可能非常大,请输出总数对 1000000007 (10^9+7)取余的结果。
输入格式:
第一行给出一个整数 N (0<N<=100),表示二叉树中元素个数;
第二行给出 N 个正整数,以空格分隔,表示二叉树的先序遍历序列;
输出格式:
在一行中输出插入序列总数。
输入样例:
6
3 2 1 4 6 5
输出样例:
10
当前子树插入序列个数N(T)=C(num_l,num_r+num_l)*N( TL )*N( TR );
num_l为左子树元素个数,num_r为右子树元素个数,N(TL)为左子树插入序列个数,N(TR)为右子树插入序列个数。后序遍历递归求N(T)。
C代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef int ElementType;
typedef struct BiTNode{
ElementType data;
long long n;
int num;
struct BiTNode *lchild;
struct BiTNode *rchild;
}BiTNode,*BiTree;
BiTree CreatBinTree(int *pre,int n );
const int N = 100 + 5;
const int MOD = (int)1e9 + 7;
int C[N][N];//C[n][m]就是C(n,m),n>m
void init(){//杨辉三角求组合数防爆必备。常规求组合数会溢出,推荐用递推式求组合数。
for(int i = 0; i < N; i ++){
C[i][0] = C[i][i] = 1;
for(int j = 1; j < i; j ++){
C[i][j] = C[i-1][j] + C[i-1][j-1];
C[i][j] %= MOD;
}
}
}
void postorder( BiTree T)//后序遍历为结点添加种类数n
{
if(T)//树不空
{
postorder(T->lchild);
postorder(T->rchild);
if(!(T->lchild)&&!(T->rchild))//叶子结点,就1种插入顺序
T->n=1;
else if((T->lchild)&&!(T->rchild))//只有左子树,插入顺序个数和左子树的一样。
T->n=T->lchild->n;
else if(!(T->lchild)&&(T->rchild))//只有右子树,插入顺序个数和右子树的一样。
T->n=T->rchild->n;
else//左右子树均存在。N(T)=C(num_l,num_r+num_l)*N( TL )*N( TR )
T->n=(T->lchild->n)*(T->rchild->n)%MOD*C[T->lchild->num+T->rchild->num][T->lchild->num]%MOD;
}
};
int main()
{
init();
BiTree T;
int prelist[101];
int length;
scanf("%d",&length);
for(int i=0;i<length;i++)
{ scanf("%d",&prelist[i]);}
prelist[length]=-1;//确定最后一个结点位置。
T=CreatBinTree(prelist,length);
postorder(T);
printf("%lld",T->n);
return 0;
}
BiTree CreatBinTree(int *pre,int n)//先序造树
{
BiTree T;
int i;
if(n<=0||pre[0]==-1) return NULL;//pre[0]==-1说明已经到了序列末尾。
T=(BiTree)malloc(sizeof(BiTNode));
T->data=pre[0];
T->n=1;
T->num=n;//num确定当前子树元素个数
for(i=1;pre[i]<pre[0];i++);//i为下一根结点位置
T->lchild=CreatBinTree(pre+1,i-1);
T->rchild=CreatBinTree(pre+i,n-i);
return T;
}

























 2124
2124

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










